5.235. longest_change
| DESCRIPTION | LINKS | GRAPH | AUTOMATON |
- Origin
- Constraint
- Arguments
- Restrictions
- Purpose
is the maximum number of consecutive variables of the collection for which constraint holds in an uninterrupted way (0 if the constraint does not hold at all). We count a change when holds; and are two consecutive variables of the collection .
- Example
-
The constraint holds since its first argument is fixed to the length of the longest subsequence of consecutive values of the collection such that two consecutive values are distinct (i.e., subsequence ).
- Typical
- Symmetry
One and the same constant can be added to the attribute of all items of .
- Arg. properties
Functional dependency: determined by and .
- See also
- Keywords
characteristic of a constraint: automaton, automaton with counters.
constraint arguments: reverse of a constraint, pure functional dependency.
constraint network structure: sliding cyclic(1) constraint network(3).
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
- Graph property(ies)
-
- Graph model
In order to specify the constraint, we use , which is the number of vertices of the largest connected component. Since the initial graph corresponds to a path, this will be the length of the longest path in the final graph.
Parts (A) and (B) of Figure 5.235.1 respectively show the initial and final graph associated with the Example slot. Since we use the graph property we show the largest connected component of the final graph. It corresponds to the longest period of uninterrupted changes: sequence that involves 4 consecutive variables.
Figure 5.235.1. Initial and final graph of the constraint
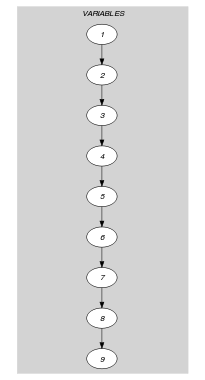
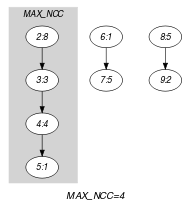
(a) (b)
- Automaton
Figure 5.235.2 depicts the automaton associated with the constraint. To each pair of consecutive variables of the collection corresponds a 0-1 signature variable . The following signature constraint links , and : .
Figure 5.235.2. Automaton of the constraint and its glue matrix
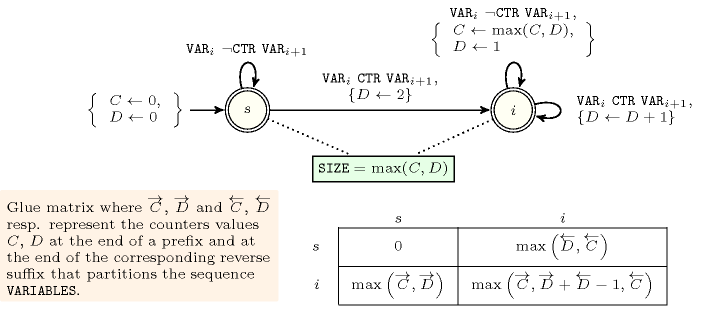
Figure 5.235.3. Hypergraph of the reformulation corresponding to the automaton of the constraint