5.401. tour
| DESCRIPTION | LINKS | GRAPH |
- Origin
- Constraint
- Synonyms
, .
- Argument
- Restrictions
- Purpose
Enforce to cover an undirected graph described by the collection with a Hamiltonian cycle.
- Example
-
The constraint holds since its argument depicts the following Hamiltonian cycle visiting successively the vertices 1, 2, 3 and 4.
- Symmetry
Items of are permutable.
- Algorithm
When the number of vertices is odd (i.e., is odd) a necessary condition is that the graph is not bipartite. Other necessary conditions for filtering the constraint are given in [Cymer13], [CymerPhD13].
- See also
common keyword: (graph partitioning constraint,Hamiltonian), (graph constraint), (constraint involving set variables).
- Keywords
characteristic of a constraint: undirected graph.
combinatorial object: matching.
constraint arguments: constraint involving set variables.
constraint type: graph constraint.
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
- Graph property(ies)
-
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
- Graph property(ies)
-
- Graph model
The first graph property enforces the subsequent condition: If we have an arc from the vertex to the vertex then we have also an arc from the vertex to the vertex. The second graph property enforces the following constraints:
We have one strongly connected component containing vertices,
Each vertex has exactly two predecessors and two successors.
Part (A) of Figure 5.401.1 shows the initial graph from which we start. It is derived from the set associated with each vertex. Each set describes the potential values of the attribute of a given vertex. Part (B) of Figure 5.401.1 gives the final graph associated with the Example slot. The constraint holds since the final graph corresponds to a Hamiltonian cycle.
Figure 5.401.1. Initial and final graph of the set constraint
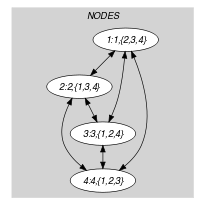
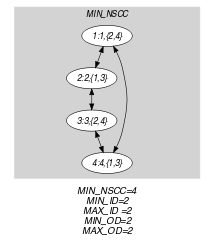
(a) (b) - Signature
Since the maximum number of vertices of the final graph is equal to , we can rewrite the graph property to and simplify to .