Global Constraint Catalog: Csoft

5.361. soft_cumulative

DESCRIPTION

LINKS

Origin

Constraint

$𝚜𝚘𝚏𝚝_𝚌𝚞𝚖𝚞𝚕𝚊𝚝𝚒𝚟𝚎 (𝚃𝙰𝚂𝙺𝚂, 𝙻𝙸𝙼𝙸𝚃, 𝙸𝙽𝚃𝙴𝚁𝙼𝙴𝙳𝙸𝙰𝚃𝙴_𝙻𝙴𝚅𝙴𝙻, 𝚂𝚄𝚁𝙵𝙰𝙲𝙴_𝙾𝙽_𝚃𝙾𝙿)$

Arguments

$𝚃𝙰𝚂𝙺𝚂$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (\begin{matrix} 𝚘𝚛𝚒𝚐𝚒𝚗 - 𝚍𝚟𝚊𝚛, \\ 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗 - 𝚍𝚟𝚊𝚛, \\ 𝚎𝚗𝚍 - 𝚍𝚟𝚊𝚛, \\ 𝚑𝚎𝚒𝚐𝚑𝚝 - 𝚍𝚟𝚊𝚛 \end{matrix})$
$𝙻𝙸𝙼𝙸𝚃$	$𝚒𝚗𝚝$
$𝙸𝙽𝚃𝙴𝚁𝙼𝙴𝙳𝙸𝙰𝚃𝙴_𝙻𝙴𝚅𝙴𝙻$	$𝚒𝚗𝚝$
$𝚂𝚄𝚁𝙵𝙰𝙲𝙴_𝙾𝙽_𝚃𝙾𝙿$	$𝚍𝚟𝚊𝚛$

Restrictions

𝚛𝚎𝚚𝚞𝚒𝚛𝚎_𝚊𝚝_𝚕𝚎𝚊𝚜𝚝

(2, 𝚃𝙰𝚂𝙺𝚂, [𝚘𝚛𝚒𝚐𝚒𝚗, 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗, 𝚎𝚗𝚍])

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚃𝙰𝚂𝙺𝚂, 𝚑𝚎𝚒𝚐𝚑𝚝)

𝚃𝙰𝚂𝙺𝚂 . 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗 \geq 0

𝚃𝙰𝚂𝙺𝚂 . 𝚘𝚛𝚒𝚐𝚒𝚗 \leq 𝚃𝙰𝚂𝙺𝚂 . 𝚎𝚗𝚍

𝚃𝙰𝚂𝙺𝚂 . 𝚑𝚎𝚒𝚐𝚑𝚝 \geq 0

𝙻𝙸𝙼𝙸𝚃 \geq 0

𝙸𝙽𝚃𝙴𝚁𝙼𝙴𝙳𝙸𝙰𝚃𝙴_𝙻𝙴𝚅𝙴𝙻 \geq 0

𝙸𝙽𝚃𝙴𝚁𝙼𝙴𝙳𝙸𝙰𝚃𝙴_𝙻𝙴𝚅𝙴𝙻 \leq 𝙻𝙸𝙼𝙸𝚃

𝚂𝚄𝚁𝙵𝙰𝙲𝙴_𝙾𝙽_𝚃𝙾𝙿 \geq 0

Purpose

Consider a set $𝒯$ of $n$ tasks described by the $𝚃𝙰𝚂𝙺𝚂$ collection, where ${𝚘𝚛𝚒𝚐𝚒𝚗}_{j}$ , ${𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗}_{j}$ , ${𝚎𝚗𝚍}_{j}$ , ${𝚑𝚎𝚒𝚐𝚑𝚝}_{j}$ are shortcuts for $𝚃𝙰𝚂𝙺𝚂 [j] . 𝚘𝚛𝚒𝚐𝚒𝚗$ , $𝚃𝙰𝚂𝙺𝚂 [j] . 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗$ , $𝚃𝙰𝚂𝙺𝚂 [j] . 𝚎𝚗𝚍$ , $𝚃𝙰𝚂𝙺𝚂 [j] . 𝚑𝚎𝚒𝚐𝚑𝚝$ . In addition let $α$ and $β$ respectively denote the earliest possible start over all tasks and the latest possible end over all tasks. The $𝚜𝚘𝚏𝚝_𝚌𝚞𝚖𝚞𝚕𝚊𝚝𝚒𝚟𝚎$ constraint forces the three following conditions:

For each task $𝚃𝙰𝚂𝙺𝚂 [j]$ $(1 \leq j \leq n)$ of $𝒯$ we have ${𝚘𝚛𝚒𝚐𝚒𝚗}_{j} + {𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗}_{j} = {𝚎𝚗𝚍}_{j}$ .
At each point in time, the cumulated height of the set of tasks that overlap that point, does not exceed a given limit $𝙻𝙸𝙼𝙸𝚃$ (i.e., $\forall i \in [α, β] : \sum_{j \in [1, n] | {𝚘𝚛𝚒𝚐𝚒𝚗}_{j} \leq i < {𝚎𝚗𝚍}_{j}} {𝚑𝚎𝚒𝚐𝚑𝚝}_{j} \leq 𝙻𝙸𝙼𝙸𝚃$ ).
The surface of the profile resource utilisation, which is greater than $𝙸𝙽𝚃𝙴𝚁𝙼𝙴𝙳𝙸𝙰𝚃𝙴_𝙻𝙴𝚅𝙴𝙻$ , is equal to $𝚂𝚄𝚁𝙵𝙰𝙲𝙴_𝙾𝙽_𝚃𝙾𝙿$ (i.e., $\sum_{i \in [α, β]} max (0, (\sum_{j \in [1, n] | {𝚘𝚛𝚒𝚐𝚒𝚗}_{j} \leq i < {𝚎𝚗𝚍}_{j}} {𝚑𝚎𝚒𝚐𝚑𝚝}_{j}) - 𝙸𝙽𝚃𝙴𝚁𝙼𝙴𝙳𝙸𝙰𝚃𝙴_𝙻𝙴𝚅𝙴𝙻)$ $=$ $𝚂𝚄𝚁𝙵𝙰𝙲𝙴_𝙾𝙽_𝚃𝙾𝙿$ ).

Example

(\begin{matrix} 〈\begin{matrix} 𝚘𝚛𝚒𝚐𝚒𝚗 - 1 & 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗 - 4 & 𝚎𝚗𝚍 - 5 & 𝚑𝚎𝚒𝚐𝚑𝚝 - 1, \\ 𝚘𝚛𝚒𝚐𝚒𝚗 - 1 & 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗 - 1 & 𝚎𝚗𝚍 - 2 & 𝚑𝚎𝚒𝚐𝚑𝚝 - 2, \\ 𝚘𝚛𝚒𝚐𝚒𝚗 - 3 & 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗 - 3 & 𝚎𝚗𝚍 - 6 & 𝚑𝚎𝚒𝚐𝚑𝚝 - 2 \end{matrix}〉, 3, 2, 3 \end{matrix})

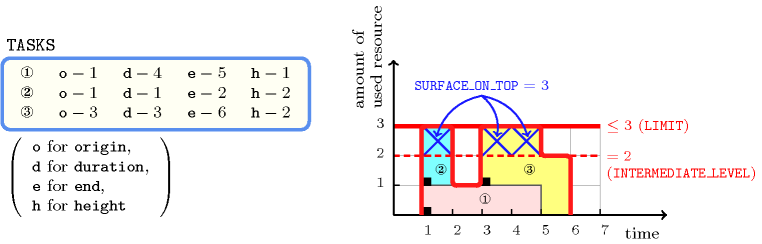
Figure 5.361.1 shows the cumulated profile associated with the example. To each task of the $𝚌𝚞𝚖𝚞𝚕𝚊𝚝𝚒𝚟𝚎$ constraint corresponds a set of rectangles coloured with the same colour: the sum of the lengths of the rectangles corresponds to the duration of the task, while the height of the rectangles (i.e., all the rectangles associated with a task have the same height) corresponds to the resource consumption of the task. The $𝚜𝚘𝚏𝚝_𝚌𝚞𝚖𝚞𝚕𝚊𝚝𝚒𝚟𝚎$ constraint holds since:

For each task we have that its end is equal to the sum of its origin and its duration.
At each point in time we do not have a cumulated resource consumption strictly greater than the upper limit $𝙻𝙸𝙼𝙸𝚃 = 3$ enforced by the second argument of the $𝚜𝚘𝚏𝚝_𝚌𝚞𝚖𝚞𝚕𝚊𝚝𝚒𝚟𝚎$ constraint.
The surface of the cumulated profile located on top of the intermediate level $𝙸𝙽𝚃𝙴𝚁𝙼𝙴𝙳𝙸𝙰𝚃𝙴_𝙻𝙴𝚅𝙴𝙻 = 2$ is equal to $𝚂𝚄𝚁𝙵𝙰𝙲𝙴_𝙾𝙽_𝚃𝙾𝙿 = 3$ .

Figure 5.361.1. Resource consumption profile associated with the three tasks of the Example slot, where parts on top of the intermediate level 2 are marked by a cross

Typical

| 𝚃𝙰𝚂𝙺𝚂 | > 1

𝚛𝚊𝚗𝚐𝚎

(𝚃𝙰𝚂𝙺𝚂 . 𝚘𝚛𝚒𝚐𝚒𝚗) > 1

𝚛𝚊𝚗𝚐𝚎

(𝚃𝙰𝚂𝙺𝚂 . 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗) > 1

𝚛𝚊𝚗𝚐𝚎

(𝚃𝙰𝚂𝙺𝚂 . 𝚎𝚗𝚍) > 1

𝚛𝚊𝚗𝚐𝚎

(𝚃𝙰𝚂𝙺𝚂 . 𝚑𝚎𝚒𝚐𝚑𝚝) > 1

𝚃𝙰𝚂𝙺𝚂 . 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗 > 0

𝚃𝙰𝚂𝙺𝚂 . 𝚑𝚎𝚒𝚐𝚑𝚝 > 0

𝙻𝙸𝙼𝙸𝚃 <

𝚜𝚞𝚖

(𝚃𝙰𝚂𝙺𝚂 . 𝚑𝚎𝚒𝚐𝚑𝚝)

𝙸𝙽𝚃𝙴𝚁𝙼𝙴𝙳𝙸𝙰𝚃𝙴_𝙻𝙴𝚅𝙴𝙻 > 0

𝙸𝙽𝚃𝙴𝚁𝙼𝙴𝙳𝙸𝙰𝚃𝙴_𝙻𝙴𝚅𝙴𝙻 < 𝙻𝙸𝙼𝙸𝚃

𝚂𝚄𝚁𝙵𝙰𝙲𝙴_𝙾𝙽_𝚃𝙾𝙿 > 0

Symmetries

Items of $𝚃𝙰𝚂𝙺𝚂$ are permutable.
One and the same constant can be added to the $𝚘𝚛𝚒𝚐𝚒𝚗$ and $𝚎𝚗𝚍$ attributes of all items of $𝚃𝙰𝚂𝙺𝚂$ .
$𝙻𝙸𝙼𝙸𝚃$ can be increased.

Remark

The $𝚜𝚘𝚏𝚝_𝚌𝚞𝚖𝚞𝚕𝚊𝚝𝚒𝚟𝚎$ constraint was initially introduced in CHIP [Cosytec97] as a variant of the $𝚌𝚞𝚖𝚞𝚕𝚊𝚝𝚒𝚟𝚎$ constraint. An extension of this constraint where one can restrict the surface on top of the intermediate level on different time intervals was first proposed in [PetitPoder09] and was generalised in [DeClercq12].

See also

hard version: $𝚌𝚞𝚖𝚞𝚕𝚊𝚝𝚒𝚟𝚎$ .

Keywords

constraint type: predefined constraint, soft constraint, scheduling constraint, resource constraint, temporal constraint, relaxation.

Global Constraint Catalog

5. Global Constraint Catalogue

5.361. soft_cumulative

Figure 5.361.1. Resource consumption profile associated with the three tasks of the Example slot, where parts on top of the intermediate level 2 are marked by a cross