- Origin
Derived from .
- Constraint
-
- Synonym
.
- Argument
| |
- Restrictions
-
- Purpose
Enforce all variables of the collection to be assigned a
value greater than or equal to 0. In addition, each value strictly
greater than 0 should appear contiguously.
- Example
-
The constraint holds since the
sequence contains
no more than one group of contiguous 1,
no more than one group of contiguous 2, and
no more than one group of contiguous 5.
- Typical
-
- Symmetry
Items of can be reversed.
- Arg. properties
Contractible wrt. .
- Counting
-
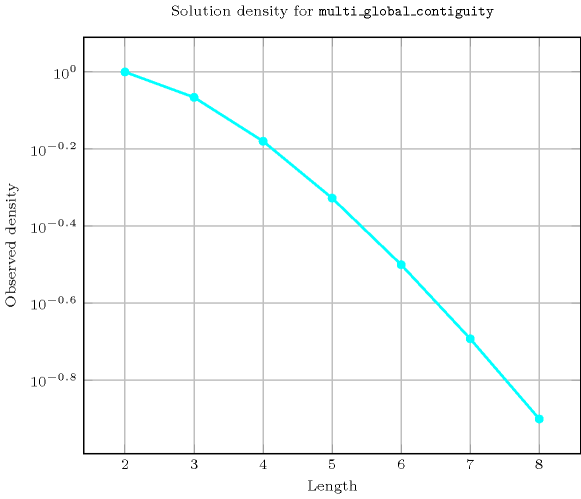
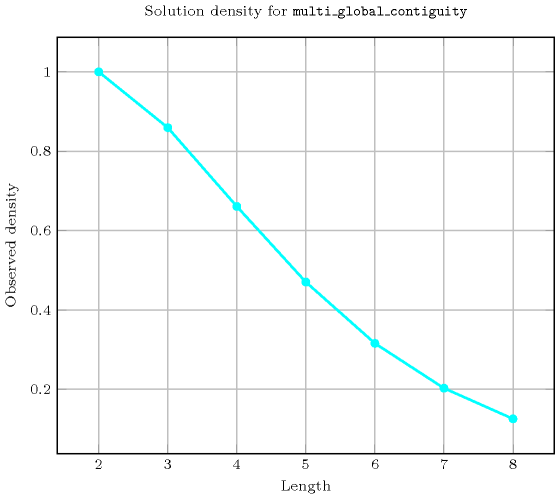
| Length () | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Solutions | 9 | 55 | 413 | 3656 | 37147 | 425069 | 5400481 |
Number of solutions for : domains
- See also
common keyword:
Β (sequence).
implied by:
,
,
,
,
,
.
- Keywords
combinatorial object:
sequence.
constraint type:
predefined constraint.
