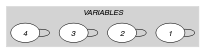
5.165. global_cardinality_low_up_no_loop
| DESCRIPTION | LINKS | GRAPH |
- Origin
- Constraint
- Synonym
.
- Arguments
- Restrictions
- Purpose
is less than or equal to the number of variables that are assigned value .
is greater than or equal to the number of variables that are assigned value .
The number of assignments of the form () is greater than or equal to and less than or equal to .
- Example
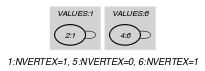
-
The constraint holds since:
Values 1, 5 and 6 are respectively assigned to the set of variables (i.e., ), (i.e., ) and (i.e., ). Note that, due to the definition of the constraint, the fact that is assigned to 1 is not counted.
In addition the number of assignments of the form () is greater than or equal to and less than or equal to .
- Typical
- Symmetries
Items of are permutable.
can be decreased to any value .
can be increased to any value .
- Usage
Within the context of the constraint the constraint allows to model a minimum and maximum degree constraint on each vertex of our trees.
- Algorithm
The flow algorithm that handles the original constraint [Regin96] can be adapted to the context of the constraint. This is done by creating an extra value node representing the loops corresponding to the roots of the trees. The rightmost part of Figure 3.7.29 illustrates the corresponding flow model for the constraint where there is a one-to-one correspondence between feasible flows in the flow model and solutions of the constraint.
- See also
generalisation: ( replaced by ).
related: (graph partitioning by a set of trees with degree restrictions).
root concept: (assignment of a to its position is ignored).
- Keywords
For all items of :
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
-
- Graph property(ies)
-
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
- Graph property(ies)
-
- Graph model
Since, within the context of the first graph constraint, we want to express one unary constraint for each value we use the “For all items of ” iterator. Part (A) of Figure 5.165.1 shows the initial graphs associated with each value 1, 5 and 6 of the collection of the Example slot. Part (B) of Figure 5.165.1 shows the two corresponding final graphs respectively associated with values 1 and 6 that are both assigned to the variables of the collection (since value 5 is not assigned to any variable of the collection the final graph associated with value 5 is empty). Since we use the graph property, the vertices of the final graphs are stressed in bold.
Figure 5.165.1. Initial and final graph of the constraint
(a) (b)