5.222. lex_between
| DESCRIPTION | LINKS | AUTOMATON |
- Origin
- Constraint
- Synonym
.
- Arguments
- Restrictions
- Purpose
The vector is lexicographically greater than or equal to the fixed vector and lexicographically smaller than or equal to the fixed vector .
- Example
-
The constraint holds since:
The vector is greater than or equal to the vector .
The vector is less than or equal to the vector .
- Typical
- Symmetries
- Arg. properties
Suffix-contractible wrt. , and (remove items from same position).
- Usage
This constraint does usually not occur explicitly in practice. However it shows up indirectly in the context of the and the constraints: in order to have a complete filtering algorithm for the and the constraints one has to come up with a complete filtering algorithm for the constraint. The reason is that the as well as the constraints both compute feasible lower and upper bounds for each vector they mention. Therefore one ends up with a constraint for each vector of the and constraints.
- Algorithm
- Reformulation
- Systems
lexChainEq in Choco, lex_chain in SICStus.
- See also
common keyword: , , , , , , (lexicographic order).
- Keywords
characteristic of a constraint: vector, automaton, automaton without counters, reified automaton constraint.
constraint network structure: Berge-acyclic constraint network.
- Automaton
Figure 5.222.1 depicts the automaton associated with the constraint. Let , and respectively be the attributes of the items of the , the and the collections. To each triple corresponds a signature variable as well as the following signature constraint:
.
Figure 5.222.1. Automaton of the constraint
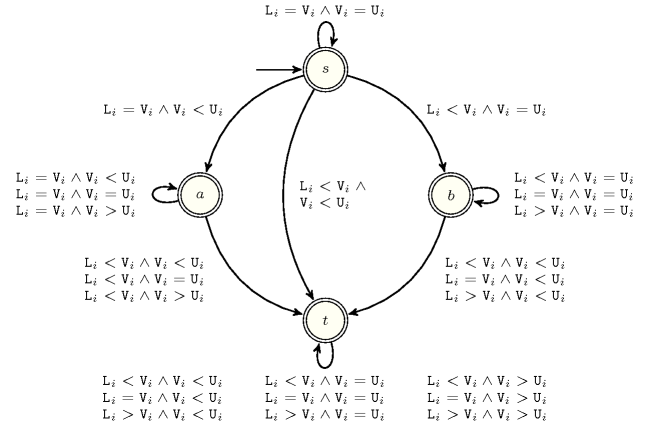
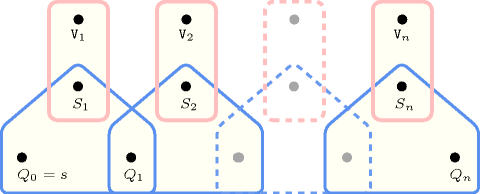
Figure 5.222.2. Hypergraph of the reformulation corresponding to the automaton of the constraint (since all states of the automaton are accepting there is no restriction on the last variable )