Global Constraint Catalog: Cint_value

5.195. int_value_precede

DESCRIPTION

LINKS

AUTOMATON

Origin

[YatChiuLawJimmyLee04]

Constraint

$𝚒𝚗𝚝_𝚟𝚊𝚕𝚞𝚎_𝚙𝚛𝚎𝚌𝚎𝚍𝚎 (𝚂, 𝚃, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

Synonyms

$𝚙𝚛𝚎𝚌𝚎𝚍𝚎$ , $𝚙𝚛𝚎𝚌𝚎𝚍𝚎𝚗𝚌𝚎$ , $𝚟𝚊𝚕𝚞𝚎_𝚙𝚛𝚎𝚌𝚎𝚍𝚎$ .

Arguments

$𝚂$	$𝚒𝚗𝚝$
$𝚃$	$𝚒𝚗𝚝$
$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛)$

Restrictions

𝚂 \neq 𝚃

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚟𝚊𝚛)

Purpose

If value $𝚃$ occurs in the collection of variables $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ then its first occurrence should be preceded by an occurrence of value $𝚂$ .

Example

(0, 1, 〈4, 0, 6, 1, 0〉)

The $𝚒𝚗𝚝_𝚟𝚊𝚕𝚞𝚎_𝚙𝚛𝚎𝚌𝚎𝚍𝚎$ constraint holds since the first occurrence of value 0 precedes the first occurrence of value 1.

Typical

𝚂 < 𝚃

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | > 1

𝚊𝚝𝚕𝚎𝚊𝚜𝚝

(1, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚂)

𝚊𝚝𝚕𝚎𝚊𝚜𝚝

(1, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚃)

Symmetries

An occurrence of a value of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛$ that is different from $𝚂$ and $𝚃$ can be replaced by any other value that is also different from $𝚂$ and $𝚃$ .
All occurrences of values $𝚂$ and $𝚃$ can be swapped in $𝚂$ , $𝚃$ and $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛$ .

Arg. properties

Suffix-contractible wrt. $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ .
Aggregate: $𝚂 (𝚒𝚍)$ , $𝚃 (𝚒𝚍)$ , $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 (𝚞𝚗𝚒𝚘𝚗)$ .

Algorithm

A filtering algorithm for maintaining value precedence is presented in [YatChiuLawJimmyLee04]. Its complexity is linear to the number of variables of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ .

Systems

precede in Gecode, value_precede in MiniZinc.

See also

generalisation: $𝚒𝚗𝚝_𝚟𝚊𝚕𝚞𝚎_𝚙𝚛𝚎𝚌𝚎𝚍𝚎_𝚌𝚑𝚊𝚒𝚗$ ( $𝚜𝚎𝚚𝚞𝚎𝚗𝚌𝚎$ of 2 $𝚟𝚊𝚕𝚞𝚎𝚜$ replaced by $𝚜𝚎𝚚𝚞𝚎𝚗𝚌𝚎$ of at least 2 $𝚟𝚊𝚕𝚞𝚎𝚜$ ), $𝚜𝚎𝚝_𝚟𝚊𝚕𝚞𝚎_𝚙𝚛𝚎𝚌𝚎𝚍𝚎$ ( $𝚜𝚎𝚚𝚞𝚎𝚗𝚌𝚎$ of $𝚍𝚘𝚖𝚊𝚒𝚗 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜$ replaced by $𝚜𝚎𝚚𝚞𝚎𝚗𝚌𝚎$ of $𝚜𝚎𝚝$ $𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜$ ).

Keywords

characteristic of a constraint: automaton, automaton without counters, reified automaton constraint.

constraint network structure: Berge-acyclic constraint network.

constraint type: order constraint.

filtering: arc-consistency.

symmetry: symmetry, indistinguishable values, value precedence.

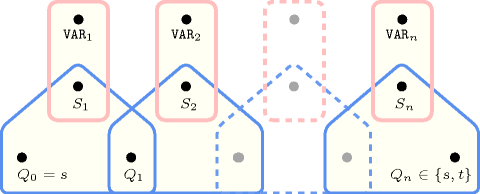
Automaton: Figure 5.195.1 depicts the automaton associated with the $𝚒𝚗𝚝_𝚟𝚊𝚕𝚞𝚎_𝚙𝚛𝚎𝚌𝚎𝚍𝚎$ constraint. Let ${𝚅𝙰𝚁}_{i}$ be the $i^{t h}$ variable of the $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ collection. To each triple $(𝚂, 𝚃, {𝚅𝙰𝚁}_{i})$ corresponds a signature variable $S_{i}$ as well as the following signature constraint: $({𝚅𝙰𝚁}_{i} = 𝚂 \Leftrightarrow S_{i} = 1) \land ({𝚅𝙰𝚁}_{i} = 𝚃 \Leftrightarrow S_{i} = 2) \land ({𝚅𝙰𝚁}_{i} \neq 𝚂 \land {𝚅𝙰𝚁}_{i} \neq 𝚃 \Leftrightarrow S_{i} = 3)$ .

Figure 5.195.1. Automaton of the $𝚒𝚗𝚝_𝚟𝚊𝚕𝚞𝚎_𝚙𝚛𝚎𝚌𝚎𝚍𝚎$ constraint (state $s$ means that value $𝚂$ was not yet encountered, while state $t$ means that value $𝚂$ was already encountered)

Figure 5.195.2. Hypergraph of the reformulation corresponding to the automaton of the $𝚒𝚗𝚝_𝚟𝚊𝚕𝚞𝚎_𝚙𝚛𝚎𝚌𝚎𝚍𝚎$ constraint

Global Constraint Catalog

5. Global Constraint Catalogue

5.195. int_value_precede

Figure 5.195.1. Automaton of the $𝚒𝚗𝚝_𝚟𝚊𝚕𝚞𝚎_𝚙𝚛𝚎𝚌𝚎𝚍𝚎$ constraint (state $s$ means that value $𝚂$ was not yet encountered, while state $t$ means that value $𝚂$ was already encountered)

Figure 5.195.2. Hypergraph of the reformulation corresponding to the automaton of the $𝚒𝚗𝚝_𝚟𝚊𝚕𝚞𝚎_𝚙𝚛𝚎𝚌𝚎𝚍𝚎$ constraint

Global Constraint Catalog

5. Global Constraint Catalogue

5.195. int_value_precede

Figure 5.195.1. Automaton of the 𝚒𝚗𝚝_𝚟𝚊𝚕𝚞𝚎_𝚙𝚛𝚎𝚌𝚎𝚍𝚎 constraint (state s means that value 𝚂 was not yet encountered, while state t means that value 𝚂 was already encountered)

Figure 5.195.2. Hypergraph of the reformulation corresponding to the automaton of the 𝚒𝚗𝚝_𝚟𝚊𝚕𝚞𝚎_𝚙𝚛𝚎𝚌𝚎𝚍𝚎 constraint

Figure 5.195.1. Automaton of the $𝚒𝚗𝚝_𝚟𝚊𝚕𝚞𝚎_𝚙𝚛𝚎𝚌𝚎𝚍𝚎$ constraint (state $s$ means that value $𝚂$ was not yet encountered, while state $t$ means that value $𝚂$ was already encountered)

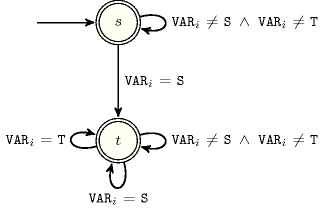
Figure 5.195.2. Hypergraph of the reformulation corresponding to the automaton of the $𝚒𝚗𝚝_𝚟𝚊𝚕𝚞𝚎_𝚙𝚛𝚎𝚌𝚎𝚍𝚎$ constraint