5.176. imply
| DESCRIPTION | LINKS | AUTOMATON |
- Origin
Logic
- Constraint
- Synonyms
, .
- Arguments
- Restrictions
- Purpose
Let be a collection of 0-1 variables . Enforce .
- Example
-
- Symmetry
All occurrences of 0 in and in can be set to 1.
- Arg. properties
Functional dependency: determined by .
- Counting
-
Length () 2 3 4 5 6 7 8 Solutions 4 0 0 0 0 0 0 Number of solutions for : domains
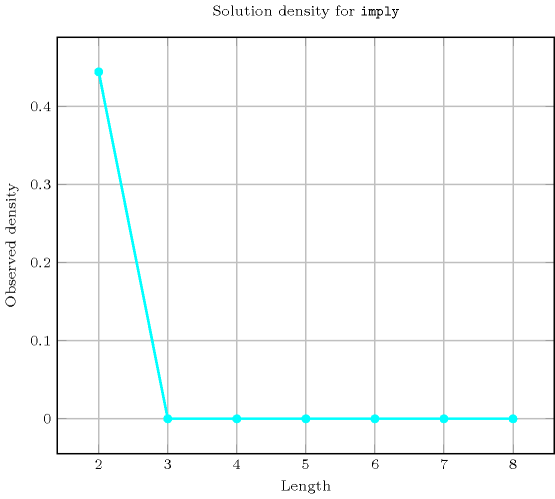
Length () 2 Total 4 Parameter value 0 1 1 3 Solution count for : domains
- Systems
reifiedLeftImp in Choco, rel in Gecode, ifthenbool in JaCoP, #=> in SICStus.
- See also
common keyword: , , , , , (Boolean constraint).
implies: , .
- Keywords
characteristic of a constraint: automaton, automaton without counters, reified automaton constraint.
constraint arguments: pure functional dependency.
constraint network structure: Berge-acyclic constraint network.
- Automaton
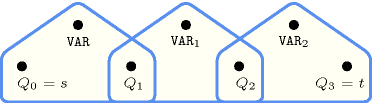
Figure 5.176.1 depicts the automaton associated with the constraint. To the first argument of the constraint corresponds the first signature variable. To each variable of the second argument of the constraint corresponds the next signature variable. There is no signature constraint.
Figure 5.176.1. Automaton of the constraint
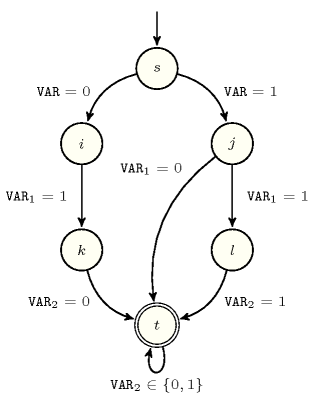
Figure 5.176.2. Hypergraph of the reformulation corresponding to the automaton of the constraint