Global Constraint Catalog: Csubgraph

5.382. subgraph_isomorphism

DESCRIPTION

LINKS

Origin

Constraint

$𝚜𝚞𝚋𝚐𝚛𝚊𝚙𝚑_𝚒𝚜𝚘𝚖𝚘𝚛𝚙𝚑𝚒𝚜𝚖 (𝙽𝙾𝙳𝙴𝚂_𝙿𝙰𝚃𝚃𝙴𝚁𝙽, 𝙽𝙾𝙳𝙴𝚂_𝚃𝙰𝚁𝙶𝙴𝚃, 𝙵𝚄𝙽𝙲𝚃𝙸𝙾𝙽)$

Arguments

$𝙽𝙾𝙳𝙴𝚂_𝙿𝙰𝚃𝚃𝙴𝚁𝙽$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚒𝚗𝚍𝚎𝚡 - 𝚒𝚗𝚝, 𝚜𝚞𝚌𝚌 - 𝚜𝚒𝚗𝚝)$
$𝙽𝙾𝙳𝙴𝚂_𝚃𝙰𝚁𝙶𝙴𝚃$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚒𝚗𝚍𝚎𝚡 - 𝚒𝚗𝚝, 𝚜𝚞𝚌𝚌 - 𝚜𝚟𝚊𝚛)$
$𝙵𝚄𝙽𝙲𝚃𝙸𝙾𝙽$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚒𝚖𝚊𝚐𝚎 - 𝚍𝚟𝚊𝚛)$

Restrictions

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝙽𝙾𝙳𝙴𝚂_𝙿𝙰𝚃𝚃𝙴𝚁𝙽, [𝚒𝚗𝚍𝚎𝚡, 𝚜𝚞𝚌𝚌])

𝙽𝙾𝙳𝙴𝚂_𝙿𝙰𝚃𝚃𝙴𝚁𝙽 . 𝚒𝚗𝚍𝚎𝚡 \geq 1

𝙽𝙾𝙳𝙴𝚂_𝙿𝙰𝚃𝚃𝙴𝚁𝙽 . 𝚒𝚗𝚍𝚎𝚡 \leq | 𝙽𝙾𝙳𝙴𝚂_𝙿𝙰𝚃𝚃𝙴𝚁𝙽 |

𝚍𝚒𝚜𝚝𝚒𝚗𝚌𝚝

(𝙽𝙾𝙳𝙴𝚂_𝙿𝙰𝚃𝚃𝙴𝚁𝙽, 𝚒𝚗𝚍𝚎𝚡)

𝙽𝙾𝙳𝙴𝚂_𝙿𝙰𝚃𝚃𝙴𝚁𝙽 . 𝚜𝚞𝚌𝚌 \geq 1

𝙽𝙾𝙳𝙴𝚂_𝙿𝙰𝚃𝚃𝙴𝚁𝙽 . 𝚜𝚞𝚌𝚌 \leq | 𝙽𝙾𝙳𝙴𝚂_𝙿𝙰𝚃𝚃𝙴𝚁𝙽 |

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝙽𝙾𝙳𝙴𝚂_𝚃𝙰𝚁𝙶𝙴𝚃, [𝚒𝚗𝚍𝚎𝚡, 𝚜𝚞𝚌𝚌])

𝙽𝙾𝙳𝙴𝚂_𝚃𝙰𝚁𝙶𝙴𝚃 . 𝚒𝚗𝚍𝚎𝚡 \geq 1

𝙽𝙾𝙳𝙴𝚂_𝚃𝙰𝚁𝙶𝙴𝚃 . 𝚒𝚗𝚍𝚎𝚡 \leq | 𝙽𝙾𝙳𝙴𝚂_𝚃𝙰𝚁𝙶𝙴𝚃 |

𝚍𝚒𝚜𝚝𝚒𝚗𝚌𝚝

(𝙽𝙾𝙳𝙴𝚂_𝚃𝙰𝚁𝙶𝙴𝚃, 𝚒𝚗𝚍𝚎𝚡)

𝙽𝙾𝙳𝙴𝚂_𝚃𝙰𝚁𝙶𝙴𝚃 . 𝚜𝚞𝚌𝚌 \geq 1

𝙽𝙾𝙳𝙴𝚂_𝚃𝙰𝚁𝙶𝙴𝚃 . 𝚜𝚞𝚌𝚌 \leq | 𝙽𝙾𝙳𝙴𝚂_𝚃𝙰𝚁𝙶𝙴𝚃 |

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝙵𝚄𝙽𝙲𝚃𝙸𝙾𝙽, [𝚒𝚖𝚊𝚐𝚎])

𝙵𝚄𝙽𝙲𝚃𝙸𝙾𝙽 . 𝚒𝚖𝚊𝚐𝚎 \geq 1

𝙵𝚄𝙽𝙲𝚃𝙸𝙾𝙽 . 𝚒𝚖𝚊𝚐𝚎 \leq | 𝙽𝙾𝙳𝙴𝚂_𝚃𝙰𝚁𝙶𝙴𝚃 |

𝚍𝚒𝚜𝚝𝚒𝚗𝚌𝚝

(𝙵𝚄𝙽𝙲𝚃𝙸𝙾𝙽, 𝚒𝚖𝚊𝚐𝚎)

| 𝙵𝚄𝙽𝙲𝚃𝙸𝙾𝙽 | = | 𝙽𝙾𝙳𝙴𝚂_𝙿𝙰𝚃𝚃𝙴𝚁𝙽 |

Purpose

Given two directed graphs $𝙿𝙰𝚃𝚃𝙴𝚁𝙽$ and $𝚃𝙰𝚁𝙶𝙴𝚃$ enforce a one to one correspondence, defined by the function $𝙵𝚄𝙽𝙲𝚃𝙸𝙾𝙽$ , between the vertices of the graph $𝙿𝙰𝚃𝚃𝙴𝚁𝙽$ and the vertices of an induced subgraph of $𝚃𝙰𝚁𝙶𝙴𝚃$ so that, if there is an arc from $u$ to $v$ in the graph $𝙿𝙰𝚃𝚃𝙴𝚁𝙽$ , then there is also an arc from the image of $u$ to the image of $v$ in the induced subgraph of $𝚃𝙰𝚁𝙶𝙴𝚃$ . The vertices of both graphs are respectively defined by the two collections of vertices $𝙽𝙾𝙳𝙴𝚂_𝙿𝙰𝚃𝚃𝙴𝚁𝙽$ and $𝙽𝙾𝙳𝙴𝚂_𝚃𝙰𝚁𝙶𝙴𝚃$ . Within collection $𝙽𝙾𝙳𝙴𝚂_𝙿𝙰𝚃𝚃𝙴𝚁𝙽$ the set of successors of each node is fixed, while this is not the case for the collection $𝙽𝙾𝙳𝙴𝚂_𝚃𝙰𝚁𝙶𝙴𝚃$ . This stems from the fact that the $𝚃𝙰𝚁𝙶𝙴𝚃$ graph is not fixed (i.e., the lower and upper bounds of the target graph are specified when we post the $𝚜𝚞𝚋𝚐𝚛𝚊𝚙𝚑_𝚒𝚜𝚘𝚖𝚘𝚛𝚙𝚑𝚒𝚜𝚖$ constraint, while the induced subgraph of a solution to the $𝚜𝚞𝚋𝚐𝚛𝚊𝚙𝚑_𝚒𝚜𝚘𝚖𝚘𝚛𝚙𝚑𝚒𝚜𝚖$ constraint corresponds to a graph for which the upper and lower bounds are identical).

Example

(\begin{matrix} 〈\begin{matrix} 𝚒𝚗𝚍𝚎𝚡 - 1 & 𝚜𝚞𝚌𝚌 - {2, 4}, \\ 𝚒𝚗𝚍𝚎𝚡 - 2 & 𝚜𝚞𝚌𝚌 - {1, 3, 4}, \\ 𝚒𝚗𝚍𝚎𝚡 - 3 & 𝚜𝚞𝚌𝚌 - \emptyset, \\ 𝚒𝚗𝚍𝚎𝚡 - 4 & 𝚜𝚞𝚌𝚌 - \emptyset \end{matrix}〉, \\ 〈\begin{matrix} 𝚒𝚗𝚍𝚎𝚡 - 1 & 𝚜𝚞𝚌𝚌 - \emptyset, \\ 𝚒𝚗𝚍𝚎𝚡 - 2 & 𝚜𝚞𝚌𝚌 - {3, 4, 5}, \\ 𝚒𝚗𝚍𝚎𝚡 - 3 & 𝚜𝚞𝚌𝚌 - \emptyset, \\ 𝚒𝚗𝚍𝚎𝚡 - 4 & 𝚜𝚞𝚌𝚌 - {2, 5}, \\ 𝚒𝚗𝚍𝚎𝚡 - 5 & 𝚜𝚞𝚌𝚌 - \emptyset \end{matrix}〉, \\ 〈4, 2, 3, 5〉 \end{matrix})

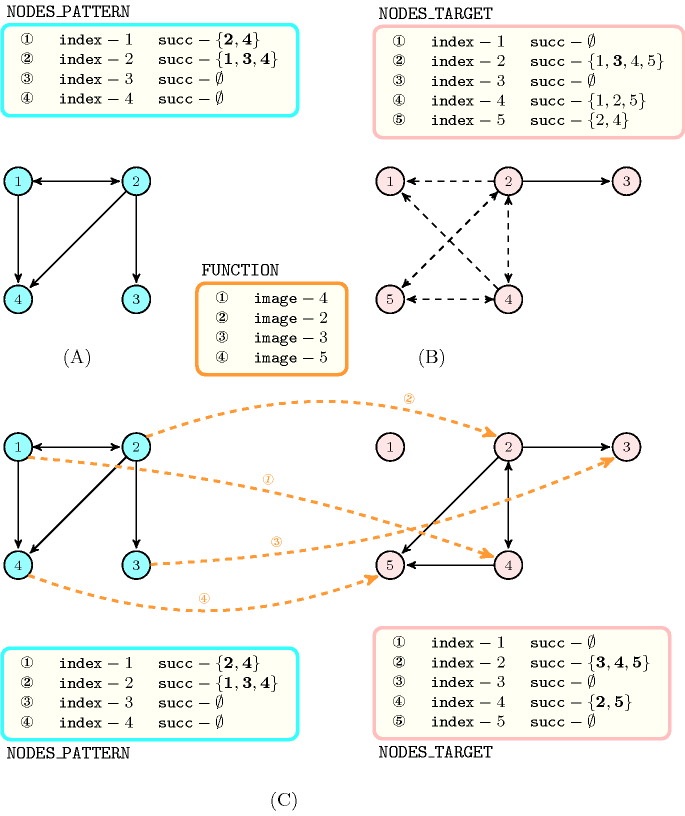
Figure 5.382.1 gives the pattern (see Part (A)) and target graph (see Part (B)) of the Example slot as well as the one to one correspondence (see Part (C)) between the pattern graph and the induced subgraph of the target graph. The $𝚜𝚞𝚋𝚐𝚛𝚊𝚙𝚑_𝚒𝚜𝚘𝚖𝚘𝚛𝚙𝚑𝚒𝚜𝚖$ constraint since:

To the arc from vertex 1 to vertex 4 in the pattern graph corresponds the arc from vertex 4 to 5 in the induced subgraph of the target graph.
To the arc from vertex 1 to vertex 2 in the pattern graph corresponds the arc from vertex 4 to 2 in the induced subgraph of the target graph.
To the arc from vertex 2 to vertex 1 in the pattern graph corresponds the arc from vertex 2 to 4 in the induced subgraph of the target graph.
To the arc from vertex 2 to vertex 4 in the pattern graph corresponds the arc from vertex 2 to 5 in the induced subgraph of the target graph.
To the arc from vertex 2 to vertex 3 in the pattern graph corresponds the arc from vertex 2 to 3 in the induced subgraph of the target graph.