Global Constraint Catalog: Call

5.10. all_incomparable

DESCRIPTION

LINKS

GRAPH

Origin

Inspired by incomparable rectangles.

Constraint

$𝚊𝚕𝚕_𝚒𝚗𝚌𝚘𝚖𝚙𝚊𝚛𝚊𝚋𝚕𝚎 (𝚅𝙴𝙲𝚃𝙾𝚁𝚂)$

Synonym

$𝚊𝚕𝚕_𝚒𝚗𝚌𝚘𝚖𝚙𝚊𝚛𝚊𝚋𝚕𝚎𝚜$ .

Type

𝚅𝙴𝙲𝚃𝙾𝚁

𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛)

Argument

𝚅𝙴𝙲𝚃𝙾𝚁𝚂

𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚎𝚌 - 𝚅𝙴𝙲𝚃𝙾𝚁)

Restrictions

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙴𝙲𝚃𝙾𝚁, 𝚟𝚊𝚛)

| 𝚅𝙴𝙲𝚃𝙾𝚁 | \geq 1

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙴𝙲𝚃𝙾𝚁𝚂, 𝚟𝚎𝚌)

| 𝚅𝙴𝙲𝚃𝙾𝚁𝚂 | \geq 1

𝚜𝚊𝚖𝚎_𝚜𝚒𝚣𝚎

(𝚅𝙴𝙲𝚃𝙾𝚁𝚂, 𝚟𝚎𝚌)

Purpose

Enforce for each pair of distinct vectors of the $𝚅𝙴𝙲𝚃𝙾𝚁𝚂$ collection the fact that they are incomparable. Two vectors $𝚅𝙴𝙲𝚃𝙾𝚁 1$ and $𝚅𝙴𝙲𝚃𝙾𝚁 2$ are incomparable if and only, when the components of both vectors are ordered, and respectively denoted by $𝚂𝚅𝙴𝙲𝚃𝙾𝚁 1$ and $𝚂𝚅𝙴𝙲𝚃𝙾𝚁 2$ , we neither have $𝚂𝚅𝙴𝙲𝚃𝙾𝚁 1 [i] . 𝚟𝚊𝚛 \leq 𝚂𝚅𝙴𝙲𝚃𝙾𝚁 2 [i] . 𝚟𝚊𝚛$ (for all $i \in [1, | 𝚂𝚅𝙴𝙲𝚃𝙾𝚁 1 |]$ ) nor have $𝚂𝚅𝙴𝙲𝚃𝙾𝚁 2 [i] . 𝚟𝚊𝚛 \leq 𝚂𝚅𝙴𝙲𝚃𝙾𝚁 1 [i] . 𝚟𝚊𝚛$ (for all $i \in [1, | 𝚂𝚅𝙴𝙲𝚃𝙾𝚁 1 |]$ ).

Example

(\begin{matrix} 〈\begin{matrix} 𝚟𝚎𝚌 - 〈1, 18〉, \\ 𝚟𝚎𝚌 - 〈2, 16〉, \\ 𝚟𝚎𝚌 - 〈3, 13〉, \\ 𝚟𝚎𝚌 - 〈4, 11〉, \\ 𝚟𝚎𝚌 - 〈5, 10〉, \\ 𝚟𝚎𝚌 - 〈6, 9〉, \\ 𝚟𝚎𝚌 - 〈7, 7〉 \end{matrix}〉 \end{matrix})

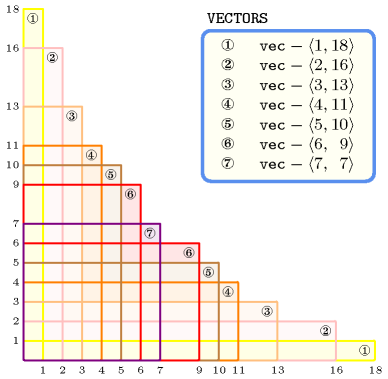
The $𝚊𝚕𝚕_𝚒𝚗𝚌𝚘𝚖𝚙𝚊𝚛𝚊𝚋𝚕𝚎$ constraint holds since all distinct pairs of vectors are incomparable as illustrated by Figure 5.10.1.

Figure 5.10.1. Illustrating the incomparability of vectors $〈 1, 18 〉$ , $〈 2, 16 〉$ , $〈 3, 13 〉$ , $〈 4, 11 〉$ , $〈 5, 10 〉$ , $〈 6, 9 〉$ , $〈 7, 7 〉$ : first to each vector we associate a rectangle whose sizes are the components of the vector; second no matter whether we rotate a rectangle from $90^{\circ}$ or not, one rectangle can not be included in another rectangle.

All solutions

Figure 5.10.2 gives all solutions to the following non ground instance of the $𝚊𝚕𝚕_𝚒𝚗𝚌𝚘𝚖𝚙𝚊𝚛𝚊𝚋𝚕𝚎$ constraint: $U_{1} \in [1, 2]$ , $V_{1} \in [0, 5]$ , $U_{2} \in [3, 5]$ , $V_{2} \in [2, 3]$ , $U_{3} \in [0, 6]$ , $V_{3} \in [2, 5]$ , $𝚊𝚕𝚕_𝚒𝚗𝚌𝚘𝚖𝚙𝚊𝚛𝚊𝚋𝚕𝚎$ $(〈 〈 U_{1}, V_{1} 〉, 〈 U_{2}, V_{2} 〉, 〈 U_{3}, V_{3} 〉 〉)$ .

Figure 5.10.2. All solutions corresponding to the non ground example of the $𝚊𝚕𝚕_𝚒𝚗𝚌𝚘𝚖𝚙𝚊𝚛𝚊𝚋𝚕𝚎$ constraint of the All solutions slot

Typical

| 𝚅𝙴𝙲𝚃𝙾𝚁 | > 1

| 𝚅𝙴𝙲𝚃𝙾𝚁𝚂 | > 1

| 𝚅𝙴𝙲𝚃𝙾𝚁𝚂 | > | 𝚅𝙴𝙲𝚃𝙾𝚁 |

Symmetry

Items of $𝚅𝙴𝙲𝚃𝙾𝚁𝚂$ are permutable.

Arg. properties

Contractible wrt. $𝚅𝙴𝙲𝚃𝙾𝚁𝚂$ .

See also

implies: $𝚕𝚎𝚡_𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝$ .

part of system of constraints: $𝚒𝚗𝚌𝚘𝚖𝚙𝚊𝚛𝚊𝚋𝚕𝚎$ .

used in graph description: $𝚒𝚗𝚌𝚘𝚖𝚙𝚊𝚛𝚊𝚋𝚕𝚎$ .

Keywords

characteristic of a constraint: vector.

constraint type: system of constraints, decomposition.

final graph structure: no loop, symmetric.

Cond. implications

$•$ $𝚊𝚕𝚕_𝚒𝚗𝚌𝚘𝚖𝚙𝚊𝚛𝚊𝚋𝚕𝚎 (𝚅𝙴𝙲𝚃𝙾𝚁𝚂)$

with $| 𝚅𝙴𝙲𝚃𝙾𝚁 | = 2$

implies $𝚔_𝚍𝚒𝚜𝚓𝚘𝚒𝚗𝚝$ $(𝚂𝙴𝚃𝚂 : 𝚅𝙴𝙲𝚃𝙾𝚁𝚂)$ .

$•$ $𝚊𝚕𝚕_𝚒𝚗𝚌𝚘𝚖𝚙𝚊𝚛𝚊𝚋𝚕𝚎 (𝚅𝙴𝙲𝚃𝙾𝚁𝚂)$

with $| 𝚅𝙴𝙲𝚃𝙾𝚁 | = 2$

implies $𝚝𝚠𝚒𝚗$ $(𝙿𝙰𝙸𝚁𝚂 : 𝚅𝙴𝙲𝚃𝙾𝚁𝚂)$ .

Arc input(s)

$𝚅𝙴𝙲𝚃𝙾𝚁𝚂$

Arc generator

𝐶𝐿𝐼𝑄𝑈𝐸

(\neq) \mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚎𝚌𝚝𝚘𝚛𝚜 1, 𝚟𝚎𝚌𝚝𝚘𝚛𝚜 2)

Arc arity

Arc constraint(s)

𝚒𝚗𝚌𝚘𝚖𝚙𝚊𝚛𝚊𝚋𝚕𝚎

(𝚟𝚎𝚌𝚝𝚘𝚛𝚜 1 . 𝚟𝚎𝚌, 𝚟𝚎𝚌𝚝𝚘𝚛𝚜 2 . 𝚟𝚎𝚌)

Graph property(ies)

𝐍𝐀𝐑𝐂

= | 𝚅𝙴𝙲𝚃𝙾𝚁𝚂 | * | 𝚅𝙴𝙲𝚃𝙾𝚁𝚂 | - | 𝚅𝙴𝙲𝚃𝙾𝚁𝚂 |

Graph class

•

𝙽𝙾_𝙻𝙾𝙾𝙿

•

𝚂𝚈𝙼𝙼𝙴𝚃𝚁𝙸𝙲

Graph model

The Arc constraint(s) slot uses the $𝚒𝚗𝚌𝚘𝚖𝚙𝚊𝚛𝚊𝚋𝚕𝚎$ constraint defined in this catalogue.

Parts (A) and (B) of Figure 5.10.3 respectively show the initial and final graph associated with the Example slot. Since we use the $𝐍𝐀𝐑𝐂$ graph property, the arcs of the final graph are stressed in bold. The previous constraint holds since exactly $3 \cdot (3 - 1) = 6$ arc constraints hold.

Figure 5.10.3. Initial and final graph of the $𝚊𝚕𝚕_𝚒𝚗𝚌𝚘𝚖𝚙𝚊𝚛𝚊𝚋𝚕𝚎$ constraint


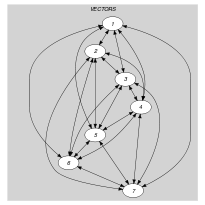
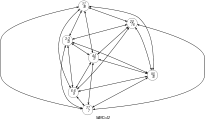
(a)	(b)

Global Constraint Catalog

5. Global Constraint Catalogue

5.10. all_incomparable

Figure 5.10.2. All solutions corresponding to the non ground example of the 𝚊𝚕𝚕_𝚒𝚗𝚌𝚘𝚖𝚙𝚊𝚛𝚊𝚋𝚕𝚎 constraint of the All solutions slot

Figure 5.10.3. Initial and final graph of the 𝚊𝚕𝚕_𝚒𝚗𝚌𝚘𝚖𝚙𝚊𝚛𝚊𝚋𝚕𝚎 constraint

Figure 5.10.2. All solutions corresponding to the non ground example of the $𝚊𝚕𝚕_𝚒𝚗𝚌𝚘𝚖𝚙𝚊𝚛𝚊𝚋𝚕𝚎$ constraint of the All solutions slot

Figure 5.10.3. Initial and final graph of the $𝚊𝚕𝚕_𝚒𝚗𝚌𝚘𝚖𝚙𝚊𝚛𝚊𝚋𝚕𝚎$ constraint