5.138. elem_from_to
| DESCRIPTION | LINKS | AUTOMATON |
- Origin
- Constraint
- Synonym
.
- Arguments
- Restrictions
- Purpose
Let , , , , respectively denote the attributes , , , , of the unique item of the collection.
Beside imposing the fact that and that both and are assigned a value in , the constraint forces the following condition: All entries of the collection from position to position are equal to . When is strictly greater than the constraint holds no matter what value is assigned to .
- Example
-
The constraint holds since all entries between position and position are equal to 2.
- Typical
- Symmetry
All occurrences of two distinct values in or can be swapped; all occurrences of a value in or can be renamed to any unused value.
- Usage
Given an array of integers (i.e., an array of integers for which the entries are defined between 1 and ), the constraint is for instance useful for encoding expressions of the form . Note that, when the interval is empty, the condition is satisfied and is equal to . This example is encoded by using an constraint and by respectively setting:
to , where is a variable that is assigned a value from interval ,
to constant 1,
to , the index of the last entry of the array ,
to constant 0,
to 0, the value we are looking for.
to the array of integers .
Finally, note that is not used at all.
- See also
- Keywords
characteristic of a constraint: automaton, automaton without counters, reified automaton constraint.
constraint type: data constraint.
modelling: array constraint, table, variable indexing, variable subscript.
- Automaton
Figure 5.138.1 depicts the automaton associated with the constraint.
Let us first introduce some notations:
Let denote the number of items of the collection.
Let and respectively be the and the attributes of the item of the collection.
Let , , , , respectively denote the attributes , , , , of the unique item of the collection.
Let be a shortcut for condition .
Let and respectively denote the quantities and .
To each septuple corresponds a signature variable as well as the following signature constraint:
.
Figure 5.138.1. Automaton of the constraint
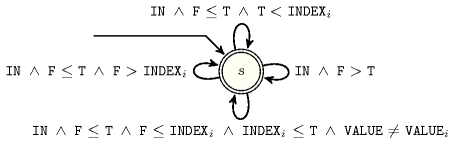
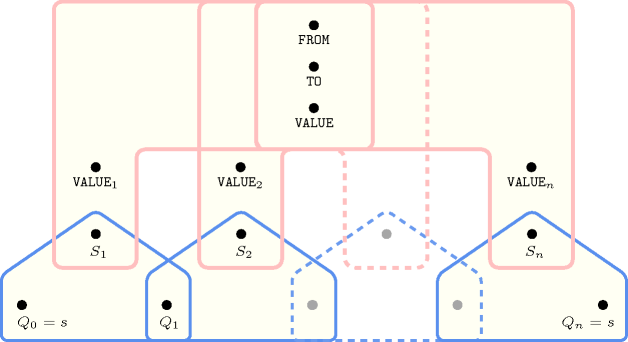
Figure 5.138.2. Hypergraph of the reformulation corresponding to the automaton of the constraint