Global Constraint Catalog: Chighest

5.175. highest_peak

DESCRIPTION

LINKS

AUTOMATON

Origin

Derived from $𝚙𝚎𝚊𝚔$ .

Constraint

$𝚑𝚒𝚐𝚑𝚎𝚜𝚝_𝚙𝚎𝚊𝚔 (𝙷𝙴𝙸𝙶𝙷𝚃, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

Arguments

$𝙷𝙴𝙸𝙶𝙷𝚃$	$𝚍𝚟𝚊𝚛$
$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛)$

Restriction

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚟𝚊𝚛)

Purpose

A variable $V_{k}$ $(1 < k < m)$ of the sequence of variables $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 = V_{1}, \dots, V_{m}$ is a peak if and only if there exists an $i$ $(1 < i \leq k)$ such that $V_{i - 1} < V_{i}$ and $V_{i} = V_{i + 1} = \dots = V_{k}$ and $V_{k} > V_{k + 1}$ . $𝙷𝙴𝙸𝙶𝙷𝚃$ is the maximum value of the peak variables. If no such variable exists $𝙷𝙴𝙸𝙶𝙷𝚃$ is equal to $𝙼𝙸𝙽𝙸𝙽𝚃$ .

Example

(8, 〈1, 1, 4, 8, 6, 2, 7, 1〉)

(1, 〈0, 1, 1, 0, 0, 1, 0, 1〉)

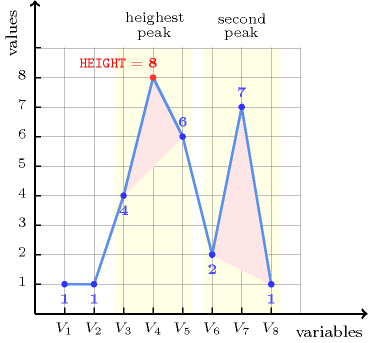
The first $𝚑𝚒𝚐𝚑𝚎𝚜𝚝_𝚙𝚎𝚊𝚔$ constraint holds since 8 is the maximum peak of the sequence $11486271$ .

Figure 5.175.1. Illustration of the first constraint of the Example slot: a sequence of eight variables $V_{1}$ , $V_{2}$ , $V_{3}$ , $V_{4}$ , $V_{5}$ , $V_{6}$ , $V_{7}$ , $V_{8}$ respectively fixed to values 1, 1, 4, 8, 6, 2, 7, 1 and its corresponding highest peak 8

Typical

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | > 2

𝚛𝚊𝚗𝚐𝚎

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛) > 2

𝚙𝚎𝚊𝚔

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛) > 0

Symmetry

Items of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ can be reversed.

Arg. properties

Functional dependency: $𝙷𝙴𝙸𝙶𝙷𝚃$ determined by $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ .

Counting

Length ( $n$ )	2	3	4	5	6	7	8
Solutions	9	64	625	7776	117649	2097152	43046721

Number of solutions for $𝚑𝚒𝚐𝚑𝚎𝚜𝚝_𝚙𝚎𝚊𝚔$ : domains $0 . . n$

ctrs/highest_peak-2-tikz

ctrs/highest_peak-3-tikz

Length (

n

)

Total

625

7776

117649

2097152

43046721

Parameter

value

-1000000

295

1792

11088

69498

439791

697

5036

35443

380

3000

22632

166208

900

7587

61389

484020

176

1712

15680

138544

1195056

2900

29125

283250

2693425

50472

540576

5665896

976227

11233250

21133632

Solution count for $𝚑𝚒𝚐𝚑𝚎𝚜𝚝_𝚙𝚎𝚊𝚔$ : domains $0 . . n$

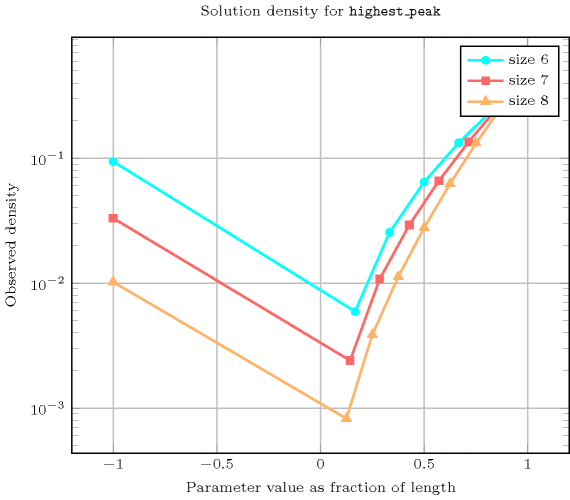
ctrs/highest_peak-4-tikz

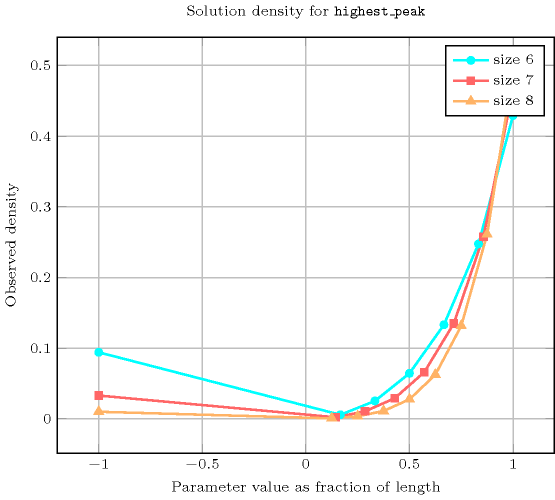
ctrs/highest_peak-5-tikz

implies: $𝚋𝚎𝚝𝚠𝚎𝚎𝚗_𝚖𝚒𝚗_𝚖𝚊𝚡$ .

Keywords

characteristic of a constraint: automaton, automaton with counters, automaton with same input symbol.

combinatorial object: sequence.

constraint arguments: reverse of a constraint, pure functional dependency.

constraint network structure: sliding cyclic(1) constraint network(2).

filtering: glue matrix.

modelling: functional dependency.

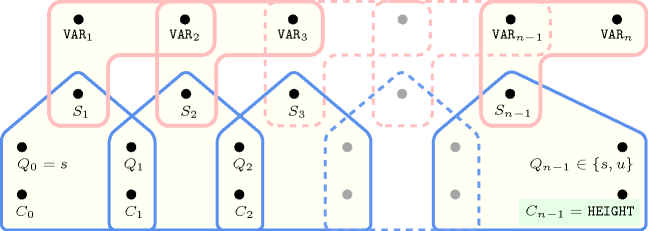
Automaton

Figure 5.175.2 depicts the automaton associated with the $𝚑𝚒𝚐𝚑𝚎𝚜𝚝_𝚙𝚎𝚊𝚔$ constraint. To each pair of consecutive variables $({𝚅𝙰𝚁}_{i}, {𝚅𝙰𝚁}_{i + 1})$ of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ corresponds a signature variable $S_{i}$ . The following signature constraint links ${𝚅𝙰𝚁}_{i}$ , ${𝚅𝙰𝚁}_{i + 1}$ and $S_{i}$ :

${𝚅𝙰𝚁}_{i} < {𝚅𝙰𝚁}_{i + 1} \Leftrightarrow S_{i} = 0 \land {𝚅𝙰𝚁}_{i} = {𝚅𝙰𝚁}_{i + 1} \Leftrightarrow S_{i} = 1 \land {𝚅𝙰𝚁}_{i} > {𝚅𝙰𝚁}_{i + 1} \Leftrightarrow S_{i} = 2$ .

Figure 5.175.2. Automaton of the $𝚑𝚒𝚐𝚑𝚎𝚜𝚝_𝚙𝚎𝚊𝚔$ constraint and its glue matrix (state $s$ means that we are in decreasing or stationary mode, state $u$ means that we are in increasing mode, a new peak is detected each time we switch from increasing to decreasing mode and the counter $C$ is updated accordingly); $minint$ is the smallest integer that can be represented on a machine

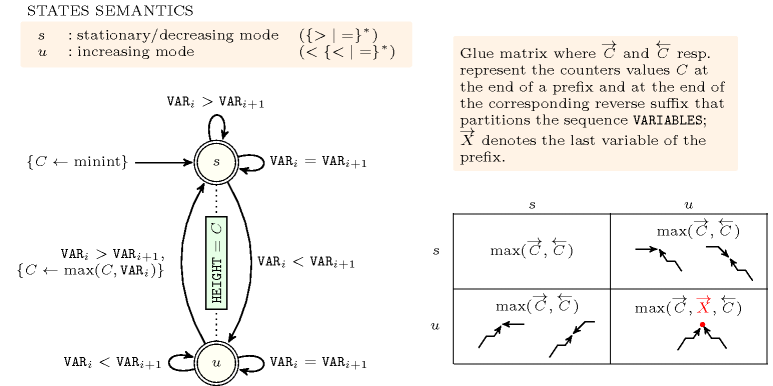
Figure 5.175.3. Hypergraph of the reformulation corresponding to the automaton of the $𝚑𝚒𝚐𝚑𝚎𝚜𝚝_𝚙𝚎𝚊𝚔$ constraint ( $C_{0}$ is set to $minint$ the largest integer that can be represented on a machine)

Global Constraint Catalog

5. Global Constraint Catalogue

5.175. highest_peak

Figure 5.175.1. Illustration of the first constraint of the Example slot: a sequence of eight variables V 1 , V 2 , V 3 , V 4 , V 5 , V 6 , V 7 , V 8 respectively fixed to values 1, 1, 4, 8, 6, 2, 7, 1 and its corresponding highest peak 8

Figure 5.175.3. Hypergraph of the reformulation corresponding to the automaton of the 𝚑𝚒𝚐𝚑𝚎𝚜𝚝_𝚙𝚎𝚊𝚔 constraint (C 0 is set to minint the largest integer that can be represented on a machine)

Figure 5.175.1. Illustration of the first constraint of the Example slot: a sequence of eight variables $V_{1}$ , $V_{2}$ , $V_{3}$ , $V_{4}$ , $V_{5}$ , $V_{6}$ , $V_{7}$ , $V_{8}$ respectively fixed to values 1, 1, 4, 8, 6, 2, 7, 1 and its corresponding highest peak 8

Figure 5.175.3. Hypergraph of the reformulation corresponding to the automaton of the $𝚑𝚒𝚐𝚑𝚎𝚜𝚝_𝚙𝚎𝚊𝚔$ constraint ( $C_{0}$ is set to $minint$ the largest integer that can be represented on a machine)