5.355. smooth
| DESCRIPTION | LINKS | GRAPH | AUTOMATON |
- Origin
- Constraint
- Arguments
- Restrictions
- Purpose
is the number of times that holds; and correspond to consecutive variables of the collection .
- Example
-
In the example we have one change between values 5 and 2 since the difference in absolute value is greater than the tolerance (i.e., ). Consequently the argument is fixed to 1 and the constraint holds.
- Typical
- Symmetries
- Arg. properties
Functional dependency: determined by and .
Prefix-contractible wrt. when .
Suffix-contractible wrt. when .
Prefix-contractible wrt. when .
Suffix-contractible wrt. when .
- Usage
This constraint is useful for the following problems:
Assume that corresponds to the number of people that work on consecutive weeks. One may not normally increase or decrease too drastically the number of people from one week to the next week. With the constraint you can state a limit on the number of drastic changes.
Assume you have to produce a set of orders, each order having a specific attribute. You want to generate the orders in such a way that there is not a too big difference between the values of the attributes of two consecutive orders. If you cannot achieve this on two given specific orders, this would imply a set-up or a cost. Again, with the constraint, you can control this kind of drastic changes.
- Algorithm
A first incomplete algorithm is described in [BeldiceanuCarlsson01]. The sketch of a filtering algorithm for the conjunction of the and the constraints based on dynamic programming achieving arc-consistency is mentioned by Lars Hellsten in [Hellsten04].
- Reformulation
The constraint can be reformulated with the constraint [PetitBeldiceanuLorca11] that we now introduce. Given a domain variable, a sequence of domain variables, and and two binary constraints, holds if (1) is equal to the number of -stretches in the sequence , and (2) holds on any pair of consecutive variables in . A -stretch is a generalisation of the notion of stretch introduced by G. Pesant [Pesant01], where the equality constraint is made explicit by replacing it by a binary constraint , i.e., a -stretch is a maximal length subsequence of for which the binary constraint is satisfied on consecutive variables. can be reformulated as , where is the universal constraint.
- See also
common keyword: (number of changes in a sequence with respect to a binary constraint).
related: .
- Keywords
characteristic of a constraint: automaton, automaton with counters, non-deterministic automaton, non-deterministic automaton.
constraint arguments: pure functional dependency.
constraint network structure: sliding cyclic(1) constraint network(2), Berge-acyclic constraint network.
constraint type: timetabling constraint.
filtering: glue matrix, dynamic programming.
modelling: number of changes, functional dependency.
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
- Graph property(ies)
-
- Graph model
Parts (A) and (B) of Figure 5.355.1 respectively show the initial and final graph associated with the Example slot. Since we use the graph property, the unique arc of the final graph is stressed in bold.
Figure 5.355.1. Initial and final graph of the constraint
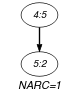
(a) (b)
- Automaton
Figure 5.355.2 depicts a first automaton that only accepts all the solutions to the constraint. This automaton uses a counter in order to record the number of satisfied constraints of the form already encountered. To each pair of consecutive variables of the collection corresponds a 0-1 signature variable . The following signature constraint links , and : .
Figure 5.355.2. Automaton (with one counter) of the constraint and its glue matrix

Figure 5.355.3. Hypergraph of the reformulation corresponding to the automaton (with one counter) of the constraint
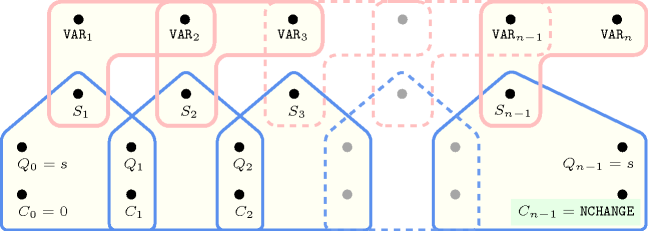
Since the reformulation associated with the previous automaton is not Berge-acyclic, we now describe a second counter free automaton that also only accepts all the solutions to the constraint. Without loss of generality, assume that the collection of variables contains at least two variables (i.e., ). Let , , , and respectively denote the number of variables of the collection , the smallest value that can be assigned to the variables of , the largest value that can be assigned to the variables of , and the union of the domains of the variables of . Clearly, the maximum number of changes (i.e., the number of times the constraint holds) cannot exceed the quantity . The states of the automaton that only accepts all the solutions to the constraint are defined in the following way:
We have an initial state labelled by .
We have intermediate states labelled by . The first subscript of state corresponds to the value currently encountered. The second subscript denotes the number of already encountered satisfied constraints of the form from the initial state to the state .
We have an accepting state labelled by .
Four classes of transitions are respectively defined in the following way:
There is a transition, labelled by from the initial state to the state , .
There is a transition, labelled by , from every state , , to the accepting state .
there is a transition labelled by from to (i.e., the counter does not change for values that are too closed from value ).
there is a transition labelled by from to (i.e., the counter is incremented by for values that are too far from ).
We have transitions of type 1, transitions of type 2, and at least transitions of types 3 and 4. Since the maximum value of is equal to , in the worst case we have at least transitions. This leads to a worst case time complexity of if we use Pesant's algorithm for filtering the constraint [Pesant04].
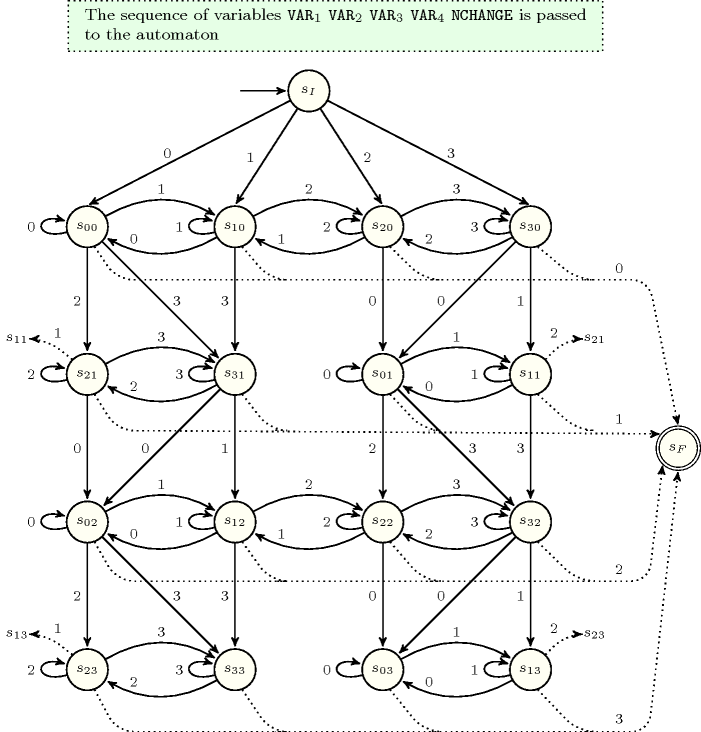
Figure 5.355.4 depicts the corresponding counter free non deterministic automaton associated with the constraint under the hypothesis that (1) all variables of are assigned a value in , (2) is equal to 4, and (3) is equal to 1.
Figure 5.355.4. Counter free non deterministic automaton of the constraint assuming , with initial state and accepting state