Global Constraint Catalog: Cused

5.412. used_by

DESCRIPTION

LINKS

GRAPH

AUTOMATON

Origin

N. Beldiceanu

Constraint

$𝚞𝚜𝚎𝚍_𝚋𝚢 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2)$

Arguments

$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛)$
$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛)$

Restrictions

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 | \geq | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 |

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1, 𝚟𝚊𝚛)

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2, 𝚟𝚊𝚛)

Purpose

All the values of the variables of collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ are used by the variables of collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ .

Example

(〈1, 9, 1, 5, 2, 1〉, 〈1, 1, 2, 5〉)

The $𝚞𝚜𝚎𝚍_𝚋𝚢$ constraint holds since, for each value occurring within the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 = 〈 1, 1, 2, 5 〉$ , its number of occurrences within $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 = 〈 1, 9, 1, 5, 2, 1 〉$ is greater than or equal to its number of occurrences within $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ :

Value 1 occurs 3 times within $〈 1, 9, 1, 5, 2, 1 〉$ and 2 times within $〈 1, 1, 2, 5 〉$ .
Value 2 occurs 1 times within $〈 1, 9, 1, 5, 2, 1 〉$ and 1 times within $〈 1, 1, 2, 5 〉$ .
Value 5 occurs 1 times within $〈 1, 9, 1, 5, 2, 1 〉$ and 1 times within $〈 1, 1, 2, 5 〉$ .

All solutions

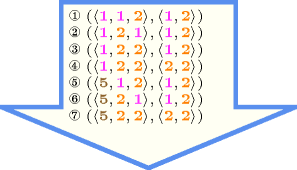
Figure 5.412.1 gives all solutions to the following non ground instance of the $𝚞𝚜𝚎𝚍_𝚋𝚢$ constraint: $U_{1} \in {1, 5}$ , $U_{2} \in [1, 2]$ , $U_{3} \in [1, 2]$ , $V_{1} \in [0, 2]$ , $V_{2} \in [2, 4]$ , $𝚞𝚜𝚎𝚍_𝚋𝚢$ $(〈 U_{1}, U_{2}, U_{3} 〉, 〈 V_{1}, V_{2} 〉)$ .

Figure 5.412.1. All solutions corresponding to the non ground example of the $𝚞𝚜𝚎𝚍_𝚋𝚢$ constraint of the All solutions slot where identical values are coloured in the same way in both collections

Typical

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 | > 1

𝚛𝚊𝚗𝚐𝚎

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 . 𝚟𝚊𝚛) > 1

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 | > 1

𝚛𝚊𝚗𝚐𝚎

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 . 𝚟𝚊𝚛) > 1

Symmetries

Items of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ are permutable.
Items of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ are permutable.
All occurrences of two distinct values in $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 . 𝚟𝚊𝚛$ or $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 . 𝚟𝚊𝚛$ can be swapped; all occurrences of a value in $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 . 𝚟𝚊𝚛$ or $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 . 𝚟𝚊𝚛$ can be renamed to any unused value.

Arg. properties

Contractible wrt. $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ .
Extensible wrt. $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ .
Aggregate: $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 (𝚞𝚗𝚒𝚘𝚗)$ , $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 (𝚞𝚗𝚒𝚘𝚗)$ .

Algorithm

As described in [BeldiceanuKatrielThiel04a] we can pad $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ with dummy variables such that its cardinality will be equal to that cardinality of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ . The domain of a dummy variable contains all of the values. Then, we have a $𝚜𝚊𝚖𝚎$ constraint between the two sets. Direct arc-consistency and bound-consistency algorithms based on a flow model are also proposed in [BeldiceanuKatrielThiel04a], [BeldiceanuKatrielThiel05], [Katriel05]. The leftmost part of Figure 3.7.30 illustrates this flow model.

More recently [Cymer12], [CymerPhD13] presents a second filtering algorithm also achieving arc-consistency based on a mapping of the solutions to the $𝚞𝚜𝚎𝚍_𝚋𝚢$ constraint to var-perfect matchingsA var-perfect matching is a maximum matching covering all vertices corresponding to the variables of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ . in a bipartite intersection graph derived from the domain of the variables of the constraint in the following way. To each variable of the $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ and $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ collection corresponds a vertex of the intersection graph. There is an edge between a vertex associated with a variable of the $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ collection and a vertex associated with a variable of the $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ collection if and only if the corresponding variables have at least one value in common in their domains.

Reformulation

The $𝚞𝚜𝚎𝚍_𝚋𝚢$ $(〈 𝚟𝚊𝚛 - U_{1} 𝚟𝚊𝚛 - U_{2}, \dots, 𝚟𝚊𝚛 - U_{| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 |} 〉, 〈 𝚟𝚊𝚛 - V_{1} 𝚟𝚊𝚛 - V_{2}, \dots, 𝚟𝚊𝚛 - V_{| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 |} 〉)$ constraint can be expressed in term of a conjunction of $| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 |$ reified constraints of the form:

$\sum_{1 \leq j \leq | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 |} (V_{i} = U_{j}) \geq \sum_{1 \leq j \leq | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 |} (V_{i} = V_{j})$ $(i \in [1, | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 |])$ .

Used in

$𝚒𝚗𝚝_𝚟𝚊𝚕𝚞𝚎_𝚙𝚛𝚎𝚌𝚎𝚍𝚎_𝚌𝚑𝚊𝚒𝚗$ , $𝚔_𝚞𝚜𝚎𝚍_𝚋𝚢$ .

See also

generalisation: $𝚞𝚜𝚎𝚍_𝚋𝚢_𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕$ ( $𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎$ replaced by $𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎 / 𝚌𝚘𝚗𝚜𝚝𝚊𝚗𝚝$ ), $𝚞𝚜𝚎𝚍_𝚋𝚢_𝚖𝚘𝚍𝚞𝚕𝚘$ ( $𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎$ replaced by $𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎 \mod 𝚌𝚘𝚗𝚜𝚝𝚊𝚗𝚝$ ), $𝚞𝚜𝚎𝚍_𝚋𝚢_𝚙𝚊𝚛𝚝𝚒𝚝𝚒𝚘𝚗$ ( $𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎$ replaced by $𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎 \in 𝚙𝚊𝚛𝚝𝚒𝚝𝚒𝚘𝚗$ ).

implied by: $𝚜𝚊𝚖𝚎$ .

implies: $𝚞𝚜𝚎𝚜$ .

soft variant: $𝚜𝚘𝚏𝚝_𝚞𝚜𝚎𝚍_𝚋𝚢_𝚟𝚊𝚛$ (variable-based violation measure).

system of constraints: $𝚔_𝚞𝚜𝚎𝚍_𝚋𝚢$ .

Keywords

characteristic of a constraint: sort based reformulation, automaton, automaton with array of counters.

combinatorial object: multiset.

constraint arguments: constraint between two collections of variables.

filtering: flow, bipartite matching, arc-consistency, bound-consistency, DFS-bottleneck.

modelling: inclusion.

Arc input(s)

$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$

Arc generator

𝑃𝑅𝑂𝐷𝑈𝐶𝑇

\mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 1, 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 2)

Arc arity

Arc constraint(s)

𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 1 . 𝚟𝚊𝚛 = 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 2 . 𝚟𝚊𝚛

Graph property(ies)

• for all connected components:

𝐍𝐒𝐎𝐔𝐑𝐂𝐄

\geq

𝐍𝐒𝐈𝐍𝐊

•

𝐍𝐒𝐈𝐍𝐊

= | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 |

Graph model

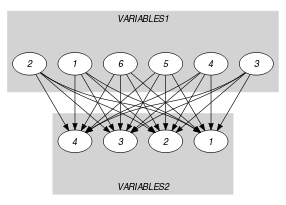
Parts (A) and (B) of Figure 5.412.2 respectively show the initial and final graph associated with the Example slot. Since we use the $𝐍𝐒𝐎𝐔𝐑𝐂𝐄$ and $𝐍𝐒𝐈𝐍𝐊$ graph properties, the source and sink vertices of the final graph are stressed with a double circle. Since there is a constraint on each connected component of the final graph we also show the different connected components. Each of them corresponds to an equivalence class according to the arc constraint. Note that the vertex corresponding to the variable assigned to value 9 was removed from the final graph since there is no arc for which the associated equality constraint holds. The $𝚞𝚜𝚎𝚍_𝚋𝚢$ constraint holds since:

For each connected component of the final graph the number of sources is greater than or equal to the number of sinks.
The number of sinks of the final graph is equal to $| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 |$ .

Figure 5.412.2. Initial and final graph of the $𝚞𝚜𝚎𝚍_𝚋𝚢$ constraint

(a)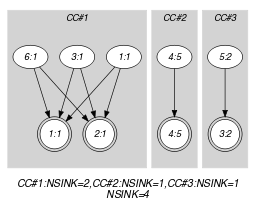

(b)

Signature

Since the initial graph contains only sources and sinks, and since sources of the initial graph cannot become sinks of the final graph, we have that the maximum number of sinks of the final graph is equal to $| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 |$ . Therefore we can rewrite $𝐍𝐒𝐈𝐍𝐊 = | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 |$ to $𝐍𝐒𝐈𝐍𝐊 \geq | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 |$ and simplify $\underset{̲}{\bar{𝐍𝐒𝐈𝐍𝐊}}$ to $\bar{𝐍𝐒𝐈𝐍𝐊}$ .

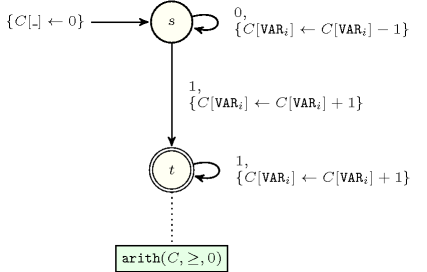
Automaton: Figure 5.412.3 depicts the automaton associated with the $𝚞𝚜𝚎𝚍_𝚋𝚢$ constraint. To each item of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ corresponds a signature variable $S_{i}$ that is equal to 0. To each item of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ corresponds a signature variable $S_{i + | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 |}$ that is equal to 1.

Figure 5.412.3. Automaton of the $𝚞𝚜𝚎𝚍_𝚋𝚢$ constraint

Global Constraint Catalog

5. Global Constraint Catalogue

5.412. used_by

Figure 5.412.1. All solutions corresponding to the non ground example of the $𝚞𝚜𝚎𝚍_𝚋𝚢$ constraint of the All solutions slot where identical values are coloured in the same way in both collections

Figure 5.412.2. Initial and final graph of the $𝚞𝚜𝚎𝚍_𝚋𝚢$ constraint

Figure 5.412.3. Automaton of the $𝚞𝚜𝚎𝚍_𝚋𝚢$ constraint

Global Constraint Catalog

5. Global Constraint Catalogue

5.412. used_by

Figure 5.412.1. All solutions corresponding to the non ground example of the 𝚞𝚜𝚎𝚍_𝚋𝚢 constraint of the All solutions slot where identical values are coloured in the same way in both collections

Figure 5.412.2. Initial and final graph of the 𝚞𝚜𝚎𝚍_𝚋𝚢 constraint

Figure 5.412.3. Automaton of the 𝚞𝚜𝚎𝚍_𝚋𝚢 constraint

Figure 5.412.1. All solutions corresponding to the non ground example of the $𝚞𝚜𝚎𝚍_𝚋𝚢$ constraint of the All solutions slot where identical values are coloured in the same way in both collections

Figure 5.412.2. Initial and final graph of the $𝚞𝚜𝚎𝚍_𝚋𝚢$ constraint

Figure 5.412.3. Automaton of the $𝚞𝚜𝚎𝚍_𝚋𝚢$ constraint