5.358. soft_all_equal_min_var
| DESCRIPTION | LINKS | GRAPH |
- Origin
- Constraint
- Arguments
- Restrictions
- Purpose
Let be the number of occurrences of the most often assigned value to the variables of the collection. is greater than or equal to the total number of variables of the collection minus (i.e., is greater than or equal to the minimum number of variables that need to be reassigned in order to obtain a solution where all variables are assigned a same value).
- Example
-
Within the collection , 3 is the number of occurrences of the most assigned value. Consequently, the constraint holds since the argument is greater than or equal to the total number of variables 4 minus 3.
- Typical
- Symmetries
can be increased.
Items of are permutable.
All occurrences of two distinct values of can be swapped; all occurrences of a value of can be renamed to any unused value.
- Algorithm
Let denote the total number of potential values that can be assigned to the variables of the collection. In [HebrardMarxSullivanRazgon09], E. Hebrard et al. provides an filtering algorithm achieving arc-consistency on the constraint. The same paper also provides an algorithm with a lower complexity for achieving range consistency. Both algorithms are based on the following ideas:
In a first phase, they both compute an envelope of the union of the domains of the variables of the collection, i.e., an array that indicates for each potential value of , the maximum number of variables that could possibly be assigned value . Let denote the maximum value over the entries of array , and let denote the set of values which all occur in variables of the collection. The quantity is a lower bound of .
In a second phase, depending on the relative ordering between and the minimum value of , i.e., , we have the three following cases:
When , the constraint simply fails since not enough variables of the collection can be assigned the same value.
When , the constraint can be satisfied. In this context, a value can be removed from the domain of a variable of the collection if and only if:
value does not belong to ,
the domain of variable contains all values of .
On the one hand, the first condition can be understand as the fact that value is not a value that allows to have at least variables assigned the same value. On the other hand, the second condition can be interpreted as the fact that variable is absolutely required in order to have at least variables assigned the same value.
When , the constraint can be satisfied, but no value can be pruned.
Note that, in the context of range consistency, the first phase of the filtering algorithm can be interpreted as a sweep algorithm were:
On the one hand, the sweep status corresponds to the maximum number of occurrence of variables that can be assigned a given value.
On the other hand, the event point series correspond to the minimum values of the variables of the collection as well as to the maximum values () of the same variables.
Figure 5.358.1. Illustration of the two phases filtering algorithm of the constraint with , , and
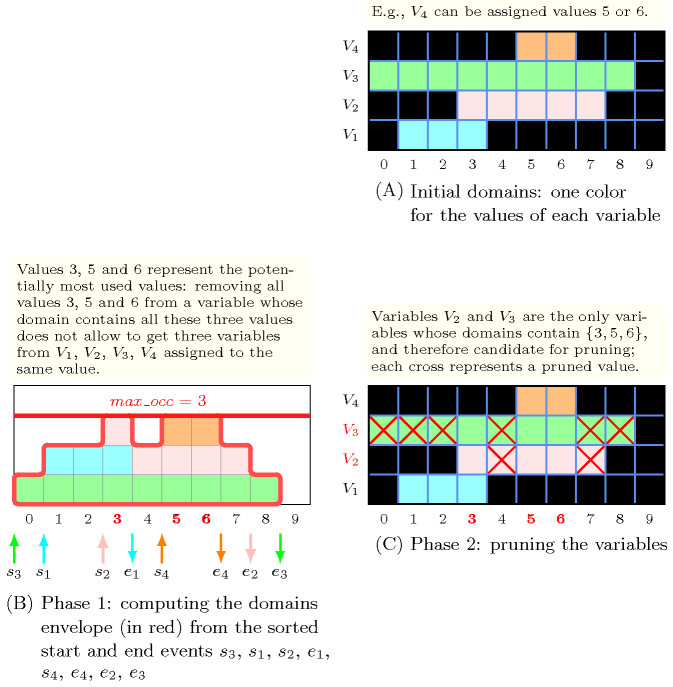
Figure 5.358.1 illustrates the previous filtering algorithm on an example where is equal to 1, and where we have four variables , , and respectively taking their values within intervals , , and (see Part (A) of Figure 5.358.1, where the values of each variable are assigned a same colour that we retrieve in the other parts of Figure 5.358.1).
Part (B) of Figure 5.358.1 illustrates the first phase of the filtering algorithm, namely the computation of the envelope of the domains of variables , , and . The start events , , , (i.e., the events respectively associated with the minimum value of variables , , , ) where the envelope is increased by 1 are represented by the character . Similarly, the end events (i.e., the events , , , respectively associated with the maximum value () of , , , are represented by the character ). Since the highest peak of the envelope is equal to 3 we have that is equal to 3. The values that allow to reach this highest peak are equal to (i.e., shown in red in Part (B) of Figure 5.358.1).
Finally, Part (C) of Figure 5.358.1 illustrates the second phase of the filtering algorithm. Since is equal to we remove from the variables whose domains contain (i.e., variables and ) all values not in (i.e., values 4, 7 for variable and values 0, 1, 2, 4, 7, 8 for variable ).
- Counting
-
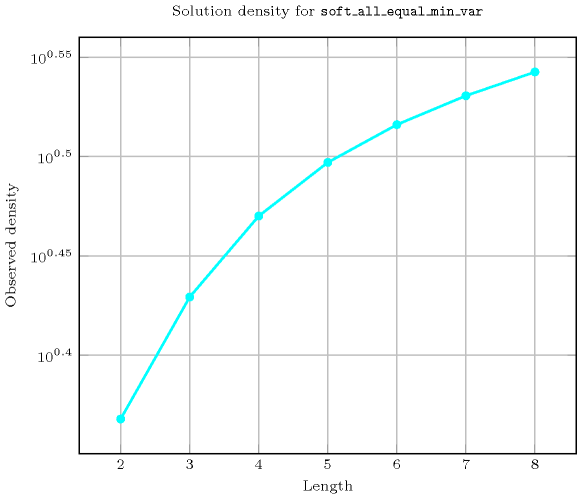
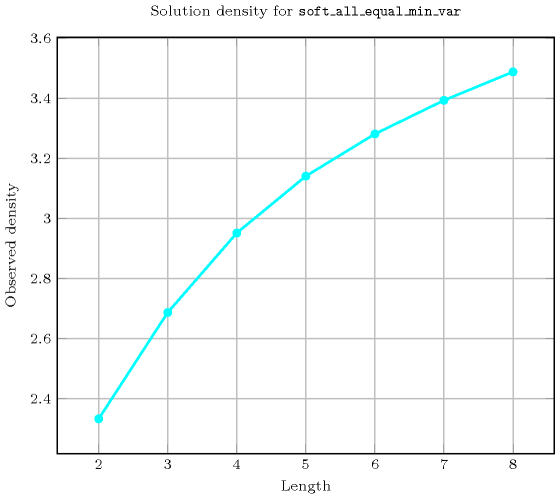
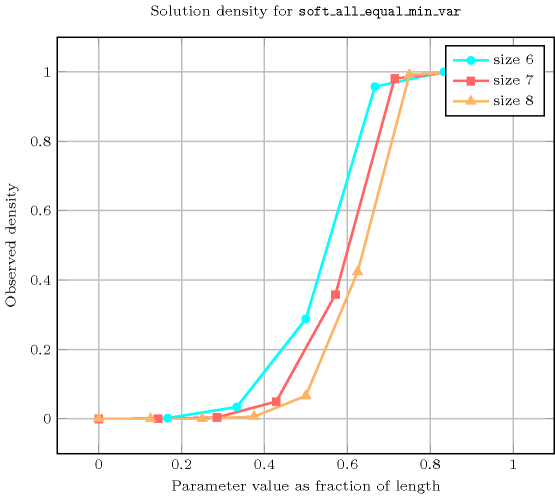
Length () 2 3 4 5 6 7 8 Solutions 21 172 1845 24426 386071 7116320 150156873 Number of solutions for : domains
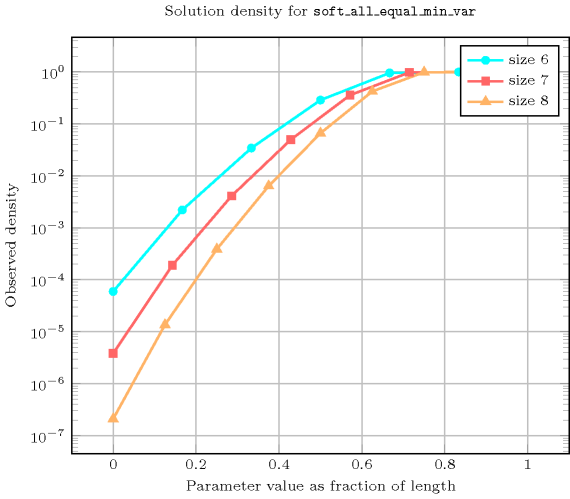
Length () 2 3 4 5 6 7 8 Total 21 172 1845 24426 386071 7116320 150156873 Parameter value 0 3 4 5 6 7 8 9 1 9 40 85 156 259 400 585 2 9 64 505 1656 4039 8632 16713 3 - 64 625 7056 33859 104672 274761 4 - - 625 7776 112609 751472 2852721 5 - - - 7776 117649 2056832 18234801 6 - - - - 117649 2097152 42683841 7 - - - - - 2097152 43046721 8 - - - - - - 43046721 Solution count for : domains
- See also
common keyword: , , , (soft constraint).
related: .
- Keywords
constraint type: soft constraint, value constraint, relaxation, variable-based violation measure.
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
- Graph property(ies)
-
- Graph model
We generate an initial graph with binary equalities constraints between each vertex and its successors. The graph property states that is greater than or equal to the difference between the total number of vertices of the initial graph and the number of vertices of the largest strongly connected component of the final graph.
Parts (A) and (B) of Figure 5.358.2 respectively show the initial and final graph associated with the Example slot. Since we use the graph property we show one of the largest strongly connected components of the final graph.
Figure 5.358.2. Initial and final graph of the constraint
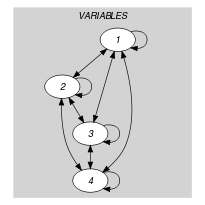
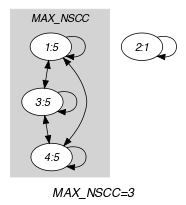
(a) (b)