[ElbassioniKatrielKutzMahajan05]

$𝚔\_\mathrm{𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝}\left(\mathrm{𝚅𝙰𝚁𝚂}\right)$

$𝚔\_\mathrm{𝚊𝚕𝚕𝚍𝚒𝚏𝚏}$, $𝚔\_\mathrm{𝚊𝚕𝚕𝚍𝚒𝚜𝚝𝚒𝚗𝚌𝚝}$, $\mathrm{𝚜𝚘𝚖𝚎}\_\mathrm{𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝}$.

The $𝚔\_\mathrm{𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝}$ constraint holds since all the values 5, 6, 0, 9 and 3 are distinct and since all the values 5, 6, 1 and 2 are distinct as well.

• Items of $\mathrm{𝚅𝙰𝚁𝚂}$ are permutable.

• Items of $\mathrm{𝚅𝙰𝚁𝚂}.\mathrm{𝚟𝚊𝚛𝚜}$ are permutable.

• All occurrences of two distinct values of $\mathrm{𝚅𝙰𝚁𝚂}.\mathrm{𝚟𝚊𝚛𝚜}.𝚡$ can be swapped; all occurrences of a value of $\mathrm{𝚅𝙰𝚁𝚂}.\mathrm{𝚟𝚊𝚛𝚜}.𝚡$ can be renamed to any unused value.

Contractible wrt. $\mathrm{𝚅𝙰𝚁𝚂}$.

Systems of $\mathrm{𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝}$ constraints sharing variables occurs frequently in practice. We give 4 typical problems that can be modelled by a combination of $\mathrm{𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝}$ constraints as well as one problem where a system of $\mathrm{𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝}$ constraints provides a necessary condition.

• The graph colouring problem is to colour with a restricted number of colours the vertices of a given undirected graph in such a way that adjacent vertices are coloured with distinct colours. The problem can be modelled by a system of $\mathrm{𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝}$ constraints. All the next problems can been seen as graph colouring problems where the graphs have some specific structure.

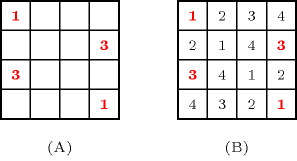
• A Latin square of order $n$ is an $n\times n$ array in which $n$ distinct numbers in $[1,n]$ are arranged so that each number occurs once in each row and column. The problem is to complete a partially filled Latin square. Part (A) of Figure 5.204.1 gives a partially filled Latin square, while part (B) provides a possible completion.

  Figure 5.204.1. (A) A partially filled Latin square and (B) a possible completion

  

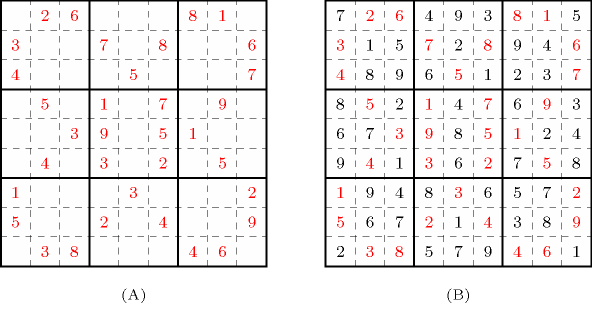
• A Sudoku is a Latin square of order $9\times 9$ such that the numbers in each major $3\times 3$ block are distinct. As for the Latin square problem, the problem is to complete a partially filled board. Part (A) of Figure 5.204.2 gives a partially filled Sudoku board, while part (B) provides a possible completion. A constraint programming approach for solving Sudoku puzzles is depicted in [Simonis05]. It shows how to generate redundant constraints as well as shaving [MartinShmoys96] in order to find a solution without guessing.

  Figure 5.204.2. (A) A partially filled Sudoku square and (B) its unique completion

  

• A task assignment problem consists to assign a given set of non-preemptive tasks, which are fixed in time (i.e., the origin, duration and end of each task are fixed), to a set of resources so that, tasks that are assigned to the same resource do not overlap in time. Each task can be assigned to a predefined set of resources. Problems like aircraft stand allocation [DincbasSimonis91], [Simonis01] or air traffic flow management [BarnierBrisset02] correspond to an example of a real-life task assignment problem. Assignment of service professionals [AsafEranRichterConnorsGreshOrtegaMcinnis10] is yet another industrial example where professionals have to be assigned positions in such a way that positions assigned to a given professional do not overlap in time.

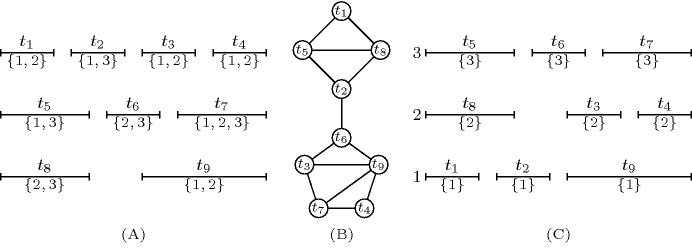
  Part (A) of Figure 5.204.3 gives an example of task assignment problem. For each task we indicate the set of resources where it can potentially be assigned (i.e., the domain of its assignment variable). For instance, task $t_1$ can be assigned to resources 1 or 2. Part (B) of Figure 5.204.3 gives the corresponding interval graph: We have one vertex for each task and an edge between two tasks that overlap in time. We have a system of $\mathrm{𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝}$ constraints corresponding to the maximum cliques of the interval graph (i.e., $\{t_1,t_5,t_8\}$, $\{t_2,t_5,t_8\}$, $\{t_2,t_6\}$, $\{t_3,t_6,t_9\}$, $\{t_3,t_7,t_9\}$, $\{t_4,t_7,t_9\}$). Finally, part (C) of Figure 5.204.3 provides a possible solution to the task assignment problem where tasks $t_1$, $t_2$, $t_9$ are assigned to resource 1, tasks $t_3$, $t_4$, $t_8$ are assigned to resource 2, and tasks $t_5$, $t_6$, $t_7$ are assigned to resource 3.

  Figure 5.204.3. (A) Tasks $t_1,t_2,\cdots ,t_9$ with their potential assignment 1, 2 or 3 (B) Interval graph where to each task of corresponds a vertex, and to each pair of overlapping tasks corresponds an edge (C) A valid assignment where tasks assigned to a same machine do not overlap

  

• The tree partitioning with precedences problem is to compute a vertex-partitioning of a given digraph $𝒢$ in disjoint trees (i.e., a forest), so that a given set of precedences holds. The problem can be modelled with a $\mathrm{𝚝𝚛𝚎𝚎}\_\mathrm{𝚙𝚛𝚎𝚌𝚎𝚍𝚎𝚗𝚌𝚎}$$(\mathrm{𝙽𝚃𝚁𝙴𝙴},\mathrm{𝚅𝙴𝚁𝚃𝙸𝙲𝙴𝚂})$ constraint, where $\mathrm{𝙽𝚃𝚁𝙴𝙴}$ is a domain variable specifying the numbers of trees in the forest and $\mathrm{𝚅𝙴𝚁𝚃𝙸𝙲𝙴𝚂}$ is a collection of the digraph's $n$ vertices. Each item $v\in \mathrm{𝚅𝙴𝚁𝚃𝙸𝙲𝙴𝚂}$ has the following attributes, which complete the description of the digraph:

  • $\mathrm{𝚒𝚗𝚍𝚎𝚡}$ is an integer in $[1,n]$ that can be interpreted as the label of $v$.

  • $\mathrm{𝚏𝚊𝚝𝚑𝚎𝚛}$ is a domain variable whose domain consists of elements (vertex label) of $[1,n]$. It can be interpreted as the unique successor of $v$.

  • $\mathrm{𝚙𝚛𝚎𝚍𝚜}$ is a possibly empty set of integers, its elements (vertex label) being in $[1,n]$. It can be interpreted as the mandatory ancestors of $v$.

  We model the $\mathrm{𝚝𝚛𝚎𝚎}\_\mathrm{𝚙𝚛𝚎𝚌𝚎𝚍𝚎𝚗𝚌𝚎}$ constraint by the digraph $𝒢=(𝒱,ℰ)$ in which the vertices represent the elements of $\mathrm{𝚅𝙴𝚁𝚃𝙸𝙲𝙴𝚂}$ and the arcs represent the successors relations between them. Formally, $𝒢$ is defined as follows:

  • To the $i^{th}$ vertex $(1\le i\le n)$, $\mathrm{𝚅𝙴𝚁𝚃𝙸𝙲𝙴𝚂}\left[i\right]$, of the $\mathrm{𝚅𝙴𝚁𝚃𝙸𝙲𝙴𝚂}$ collection corresponds a vertex of $𝒱$ denoted by $v_i$.

  • For every pair of vertices $\left(\mathrm{𝚅𝙴𝚁𝚃𝙸𝙲𝙴𝚂}\right[i]$,$\mathrm{𝚅𝙴𝚁𝚃𝙸𝙲𝙴𝚂}\left[j\right])$, where $i$ and $j$ are not necessarily distinct, there is an arc from $v_i$ to $v_j$ in $ℰ$.

  The $\mathrm{𝚝𝚛𝚎𝚎}\_\mathrm{𝚙𝚛𝚎𝚌𝚎𝚍𝚎𝚗𝚌𝚎}$ constraint specifies that its associated digraph $𝒢$ should be a forest that fulfils the precedence constraints. Formally a ground instance of a $\mathrm{𝚝𝚛𝚎𝚎}\_\mathrm{𝚙𝚛𝚎𝚌𝚎𝚍𝚎𝚗𝚌𝚎}$$(\mathrm{𝙽𝚃𝚁𝙴𝙴},\mathrm{𝚅𝙴𝚁𝚃𝙸𝙲𝙴𝚂})$ constraint is satisfied if and only if the following conditions hold:

  1. $\forall i\in [1,n]:\mathrm{𝚅𝙴𝚁𝚃𝙸𝙲𝙴𝚂}\left[i\right].\mathrm{𝚒𝚗𝚍𝚎𝚡}=i$,

  2. Its associated digraph $𝒢$ consists of $\mathrm{𝙽𝚃𝚁𝙴𝙴}$ connected components,

  3. Each connected component of $𝒢$ does not contain any circuit involving more than one vertex,

  4. For every vertex $\mathrm{𝚅𝙴𝚁𝚃𝙸𝙲𝙴𝚂}\left[i\right]$ such that $j\in \mathrm{𝚅𝙴𝚁𝚃𝙸𝙲𝙴𝚂}\left[i\right].\mathrm{𝚙𝚛𝚎𝚍𝚜}$ there must be an elementary path in $𝒢$ from $\mathrm{𝚅𝙴𝚁𝚃𝙸𝙲𝙴𝚂}\left[j\right]$ to $\mathrm{𝚅𝙴𝚁𝚃𝙸𝙲𝙴𝚂}\left[i\right]$.

  We can build the following system of $\mathrm{𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝}$ constraints that corresponds to a necessary condition for the $\mathrm{𝚝𝚛𝚎𝚎}\_\mathrm{𝚙𝚛𝚎𝚌𝚎𝚍𝚎𝚗𝚌𝚎}$ constraint: To each vertex $v$ of $𝒢$, which both has no predecessors and cannot be the root of a tree, we generate an $\mathrm{𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝}$ constraint involving the father variables of those descendants of $v$ in $𝒢$ that cannot be the root of a tree.

  Figure 5.204.4. (A) A set of precedences and (D) a corresponding feasible tree where $F_i$ stands for the father of the $i^{\mathrm{𝑡ℎ}}$ vertex; (B) the $\mathrm{𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝}$ constraint associated with the source vertex 1 and (E) the satisfied precedences in red along the paths of the tree of (D); (C) the $\mathrm{𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝}$ constraint associated with the source vertex 2 and (F) the satisfied precedences in blue along the paths of the tree of (D);

  

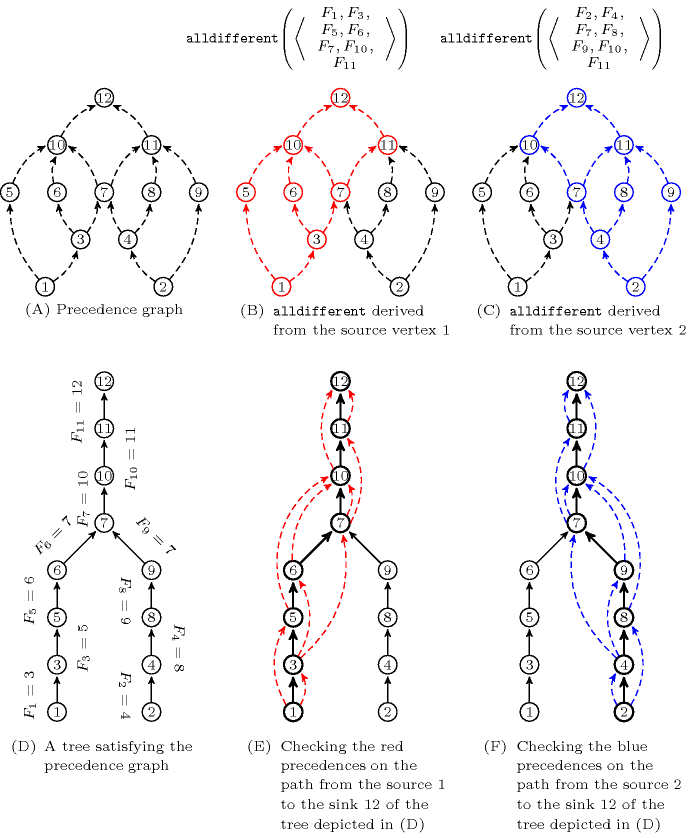
  For the set of precedences depicted by part (A) of Figure 5.204.4The number in a vertex gives the value of the $\mathrm{𝚒𝚗𝚍𝚎𝚡}$ attribute of the corresponding item., where we assume that $\mathrm{𝚅𝙴𝚁𝚃𝙸𝙲𝙴𝚂}\left[12\right]$ is the only vertex that can be a root and where $F_i$ denotes the father variable associated with $\mathrm{𝚅𝙴𝚁𝚃𝙸𝙲𝙴𝚂}\left[i\right]$, we get the following system of $\mathrm{𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝}$ constraints:

  • $\mathrm{𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝}$$\left(\langle F_1,F_3,F_5,F_6,F_7,F_{10},F_{11}\rangle \right)$,

  • $\mathrm{𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝}$$\left(\langle F_2,F_4,F_7,F_8,F_9,F_{10},F_{11}\rangle \right)$.

  The variables of these two $\mathrm{𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝}$ constraints respectively correspond to the descendants of the two source vertices (i.e., $F_1$ and $F_2$) of the precedence graph depicted by parts (B) and (C) of Figure 5.204.4. On part (B) and (C) of Figure 5.204.4 the descendants of $F_1$ and $F_2$ are respectively depicted in red and blue. Their intersection, $\{F_7,F_{10},F_{11},F_{12}\}$, from which we remove $F_{12}$ belong to the two $\mathrm{𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝}$ constraints. In fact, $F_{12}$ is not mentioned in the two $\mathrm{𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝}$ constraints since its corresponding vertex is the root of a tree. Part (D) of Figure 5.204.4 gives a possible tree satisfying all the precedences constraints expressed by part (A). It corresponds to the following ground solution:

  $\mathrm{𝚝𝚛𝚎𝚎}\_\mathrm{𝚙𝚛𝚎𝚌𝚎𝚍𝚎𝚗𝚌𝚎}$$(\langle$	$\mathrm{𝚒𝚗𝚍𝚎𝚡}-1$	$\mathrm{𝚏𝚊𝚝𝚑𝚎𝚛}-3$	$\mathrm{𝚙𝚛𝚎𝚍𝚜}-\left\{\right\},$
  	$\mathrm{𝚒𝚗𝚍𝚎𝚡}-2$	$\mathrm{𝚏𝚊𝚝𝚑𝚎𝚛}-4$	$\mathrm{𝚙𝚛𝚎𝚍𝚜}-\left\{\right\},$
  	$\mathrm{𝚒𝚗𝚍𝚎𝚡}-3$	$\mathrm{𝚏𝚊𝚝𝚑𝚎𝚛}-5$	$\mathrm{𝚙𝚛𝚎𝚍𝚜}-\left\{1\right\},$
  	$\mathrm{𝚒𝚗𝚍𝚎𝚡}-4$	$\mathrm{𝚏𝚊𝚝𝚑𝚎𝚛}-8$	$\mathrm{𝚙𝚛𝚎𝚍𝚜}-\left\{2\right\},$
  	$\mathrm{𝚒𝚗𝚍𝚎𝚡}-5$	$\mathrm{𝚏𝚊𝚝𝚑𝚎𝚛}-6$	$\mathrm{𝚙𝚛𝚎𝚍𝚜}-\left\{1\right\},$
  	$\mathrm{𝚒𝚗𝚍𝚎𝚡}-6$	$\mathrm{𝚏𝚊𝚝𝚑𝚎𝚛}-7$	$\mathrm{𝚙𝚛𝚎𝚍𝚜}-\left\{3\right\},$
  	$\mathrm{𝚒𝚗𝚍𝚎𝚡}-7$	$\mathrm{𝚏𝚊𝚝𝚑𝚎𝚛}-10$	$\mathrm{𝚙𝚛𝚎𝚍𝚜}-\{3,4\},$
  	$\mathrm{𝚒𝚗𝚍𝚎𝚡}-8$	$\mathrm{𝚏𝚊𝚝𝚑𝚎𝚛}-9$	$\mathrm{𝚙𝚛𝚎𝚍𝚜}-\left\{4\right\},$
  	$\mathrm{𝚒𝚗𝚍𝚎𝚡}-9$	$\mathrm{𝚏𝚊𝚝𝚑𝚎𝚛}-7$	$\mathrm{𝚙𝚛𝚎𝚍𝚜}-\left\{2\right\},$
  	$\mathrm{𝚒𝚗𝚍𝚎𝚡}-10$	$\mathrm{𝚏𝚊𝚝𝚑𝚎𝚛}-11$	$\mathrm{𝚙𝚛𝚎𝚍𝚜}-\{5,6,7\},$
  	$\mathrm{𝚒𝚗𝚍𝚎𝚡}-11$	$\mathrm{𝚏𝚊𝚝𝚑𝚎𝚛}-12$	$\mathrm{𝚙𝚛𝚎𝚍𝚜}-\{7,8,9\},$
  	$\mathrm{𝚒𝚗𝚍𝚎𝚡}-12$	$\mathrm{𝚏𝚊𝚝𝚑𝚎𝚛}-12$	$\mathrm{𝚙𝚛𝚎𝚍𝚜}-\{10,11\}\rangle )$

  Parts (E) and (F) of Figure 5.204.4 illustrate how the precedence constraints are satisfied by the solution depicted by part (D): each precedence, represented by a dashed arc, links two vertices that belong to a same path of the tree that is directed toward the root of the tree.

It was shown in [ElbassioniKatrielKutzMahajan05b] that, finding out whether a system of two $\mathrm{𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝}$ constraints sharing some variables has a solution or not is NP-hard. This was achieved by reduction from set packing.

A slight variation in the way of describing the arguments of the $𝚔\_\mathrm{𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝}$ constraint appears in [RichterFreundNaveh06] under the name of $\mathrm{𝚜𝚘𝚖𝚎}\_\mathrm{𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝}$: the set of disequalities is described by a set of pairs of variables, where each pair corresponds to a disequality constraint between two given variables.

Within the context of linear programming, a relaxation of the $𝚔\_\mathrm{𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝}$ constraint is provided in [AppaMagosMourtos04]. The special case where $k=2$ is discussed in [AppaMagosMourtos05].

Even if there is no filtering algorithm for the $𝚔\_\mathrm{𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝}$ constraint, one can enforce redundant constraints for the following patterns:

• Within the context of graph colouring, one can state an $\mathrm{𝚗𝚟𝚊𝚕𝚞𝚎}$ constraint for every cycle of odd length of the graph to colour enforcing that the corresponding variables have to be assigned to at least three distinct values.

• Within the context of Latin squares, one can state a $\mathrm{𝚌𝚘𝚕𝚘𝚛𝚎𝚍}\_\mathrm{𝚖𝚊𝚝𝚛𝚒𝚡}$ constraint enforcing that each value is used exactly once in each row and column.

• Within the context of two $\mathrm{𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝}$ constraints $\mathrm{𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝}$$\left(\langle U_1,\cdots ,U_n,V_1,\cdots ,V_m\rangle \right)$ and $\mathrm{𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝}$$(\langle U_1,\cdots ,U_n,$ $W_1,\cdots ,W_m\rangle )$ where the domain of all variables $U_1,\cdots ,U_n$, $V_1,\cdots ,V_m$, $W_1,\cdots ,W_m$ is included in the interval $[1,n+m]$, one can state a $\mathrm{𝚜𝚊𝚖𝚎}\_\mathrm{𝚊𝚗𝚍}\_\mathrm{𝚐𝚕𝚘𝚋𝚊𝚕}\_\mathrm{𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢}$ constraint stating that the variables $V_1,\cdots ,V_m$ should correspond to a permutation of the variables $W_1,\cdots ,W_m$ and that the variables $V_1,\cdots ,V_m$ should be assigned to distinct values.

• In the general case of two $\mathrm{𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝}$ constraints $\mathrm{𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝}$$\left(\langle U_1,\cdots ,U_n,V_1,\cdots ,V_m\rangle \right)$ and $\mathrm{𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝}$$(\langle U_1,\cdots ,U_n,$ $W_1,\cdots ,W_o\rangle )$, one can state an $\mathrm{𝚗𝚟𝚊𝚕𝚞𝚎}$ constraint involving the variables $V_1,\cdots ,V_m$ and $W_1,\cdots ,W_o$ enforcing that these variables should not use more than $s-n$ distinct values, where $s$ denotes the cardinality of the union of the domains of the variables $U_1,\cdots ,U_n$, $V_1,\cdots ,V_m$, $W_1,\cdots ,W_o$.

Several propagation rules for the $𝚔\_\mathrm{𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝}$ constraint are also described in [LardeuxMonfroySaubion08].

Given two $\mathrm{𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝}$ constraints that share some variables, a reformulation preserving bound-consistency was introduced in [BessiereKatsirelosNarodytskaQuimperWalsh10]. This reformulation is based on an extension of Hall's theorem that is presented in the same paper.

common keyword: $\mathrm{𝚌𝚘𝚕𝚘𝚛𝚎𝚍}\_\mathrm{𝚖𝚊𝚝𝚛𝚒𝚡}$ (system of constraints).

generalisation: $\mathrm{𝚍𝚒𝚏𝚏𝚗}$, $\mathrm{𝚐𝚎𝚘𝚜𝚝}$ (tasks for which the start attribute is not fixed).

part of system of constraints: $\mathrm{𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝}$.

related: $\mathrm{𝚗𝚟𝚊𝚕𝚞𝚎}$ (implied by two overlapping $\mathrm{𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝}$), $\mathrm{𝚜𝚊𝚖𝚎}\_\mathrm{𝚊𝚗𝚍}\_\mathrm{𝚐𝚕𝚘𝚋𝚊𝚕}\_\mathrm{𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢}$ (implied by two overlapping $\mathrm{𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝}$ and restriction on values).

application area: air traffic management, assignment.

characteristic of a constraint: all different, disequality.

combinatorial object: permutation, Latin square.

complexity: set packing.

constraint type: system of constraints, overlapping alldifferent, value constraint, decomposition.

filtering: bound-consistency, duplicated variables.

problems: graph colouring.

puzzles: Sudoku.

For all items of $\mathrm{𝚅𝙰𝚁𝚂}$: