5.205. k_cut
| DESCRIPTION | LINKS | GRAPH |
- Origin
E. Althaus
- Constraint
- Arguments
- Restrictions
- Purpose
Select some arcs of a digraph in order to have at least connected components (an isolated vertex, i.e. a vertex without any ingoing or outgoing arc, is counted as one connected component).
- Example
-
The constraint holds since the graph corresponding to the collection contains 3 connected components (i.e., two connected components respectively involving vertices 1 and 4 and a third connected component containing the remaining vertices 2, 3 and 5), and since the first argument enforces to have at least 3 connected components.
- Typical
- Symmetries
can be decreased to any value .
Items of are permutable.
- See also
- Keywords
constraint arguments: constraint involving set variables.
constraint type: graph constraint.
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
- Graph property(ies)
-
- Graph model
holds if and correspond to the same vertex. It is used in order to enforce keeping all the vertices of the initial graph. This is because an isolated vertex counts always as one connected component. Within the context of the Example slot, part (A) of Figure 5.205.1 shows the initial graph from which we have chosen to start. It is derived from the set associated with each vertex. Each set describes the potential values of the attribute of a given vertex. Part (B) of Figure 5.205.1 gives the final graph associated with the example of the Example slot. The constraint holds since we have at least connected components in the final graph.
Figure 5.205.1. Initial and final graph of the set constraint
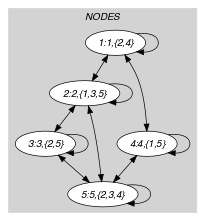
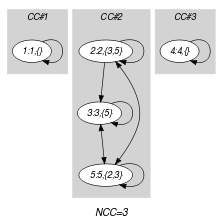
(a) (b)