5.147. elements_alldifferent
| DESCRIPTION | LINKS | GRAPH |
- Origin
- Constraint
- Synonyms
, .
- Arguments
- Restrictions
- Purpose
All the items of the collection should be equal to one of the entries of the table and all the variables should take distinct values.
- Example
-
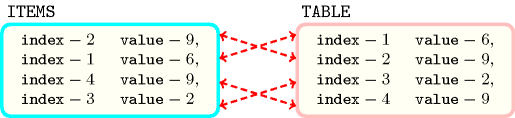
The constraint holds since, as depicted by Figure 5.147.1, there is a one to one correspondence between the items of the collection and the items of the collection.
Figure 5.147.1. Illustration of the one to one correspondence between the items of and the items of
- Typical
- Symmetries
Arguments are permutable w.r.t. permutation .
Items of are permutable.
Items of are permutable.
All occurrences of two distinct values in or can be swapped; all occurrences of a value in or can be renamed to any unused value.
- Arg. properties
Functional dependency: determined by and .
- Usage
Used for replacing by a single constraint an and a set of constraints having the following structure:
The union of the index variables of the constraints is equal to the set of variables of the constraint.
For instance, the constraint given in the Example slot is equivalent to the conjunction of the following set of constraints:
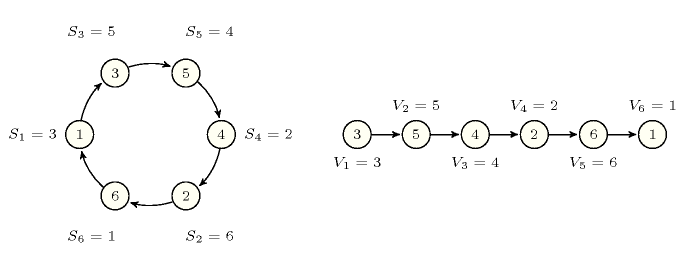
As a practical example of utilisation of the constraint we show how to model the link between a permutation consisting of a single cycle and its expanded form. For instance, to the permutation corresponds the sequence . Let us note the permutation and its expanded form (see Figure 5.147.2).
The constraint:
models the fact that corresponds to a permutation with a single cycle. It also expresses the link between the variables and .
Figure 5.147.2. Two representations of a permutation containing a single cycle
- Reformulation
The constraint can be expressed in term of a conjunction of constraints and of one constraint of the form:
- See also
implies: , .
used in reformulation: , , .
- Keywords
characteristic of a constraint: disequality.
combinatorial object: permutation.
- Cond. implications
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
-
- Graph property(ies)
-
- Graph model
The fact that all variables are pairwise different is derived from the conjunctions of the following facts:
From the graph property it follows that all vertices of the initial graph belong also to the final graph,
A vertex belongs to the final graph if there is at least one constraint involving that holds,
From the first condition of the arc constraint, and from the restriction it follows: for all vertices generated from the collection at most one constraint involving holds.
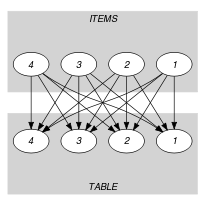
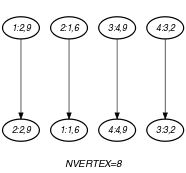
Parts (A) and (B) of Figure 5.147.3 respectively show the initial and final graph associated with the Example slot. Since we use the graph property, the vertices of the final graph are stressed in bold.
Figure 5.147.3. Initial and final graph of the constraint
(a) (b) - Signature
Since the final graph cannot have more than vertices one can simplify to .