Global Constraint Catalog: Cglobal

5.163. global_cardinality

DESCRIPTION

LINKS

GRAPH

AUTOMATON

Origin

CHARME [OplobeduMarcovitchTourbier89]

Constraint

$𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚅𝙰𝙻𝚄𝙴𝚂)$

Synonyms

$𝚌𝚘𝚞𝚗𝚝$ , $𝚍𝚒𝚜𝚝𝚛𝚒𝚋𝚞𝚝𝚎$ , $𝚍𝚒𝚜𝚝𝚛𝚒𝚋𝚞𝚝𝚒𝚘𝚗$ , $𝚐𝚌𝚌$ , $𝚌𝚊𝚛𝚍_𝚟𝚊𝚛_𝚐𝚌𝚌$ , $𝚎𝚐𝚌𝚌$ , $𝚎𝚡𝚝𝚎𝚗𝚍𝚎𝚍_𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢$ .

Arguments

$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛)$
$𝚅𝙰𝙻𝚄𝙴𝚂$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚕 - 𝚒𝚗𝚝, 𝚗𝚘𝚌𝚌𝚞𝚛𝚛𝚎𝚗𝚌𝚎 - 𝚍𝚟𝚊𝚛)$

Restrictions

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚟𝚊𝚛)

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝙻𝚄𝙴𝚂, [𝚟𝚊𝚕, 𝚗𝚘𝚌𝚌𝚞𝚛𝚛𝚎𝚗𝚌𝚎])

𝚍𝚒𝚜𝚝𝚒𝚗𝚌𝚝

(𝚅𝙰𝙻𝚄𝙴𝚂, 𝚟𝚊𝚕)

𝚅𝙰𝙻𝚄𝙴𝚂 . 𝚗𝚘𝚌𝚌𝚞𝚛𝚛𝚎𝚗𝚌𝚎 \geq 0

𝚅𝙰𝙻𝚄𝙴𝚂 . 𝚗𝚘𝚌𝚌𝚞𝚛𝚛𝚎𝚗𝚌𝚎 \leq | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 |

Purpose

Each value $𝚅𝙰𝙻𝚄𝙴𝚂 [i] . 𝚟𝚊𝚕$ (with $i \in [1, | 𝚅𝙰𝙻𝚄𝙴𝚂 |]$ ) should be taken by exactly $𝚅𝙰𝙻𝚄𝙴𝚂 [i] . 𝚗𝚘𝚌𝚌𝚞𝚛𝚛𝚎𝚗𝚌𝚎$ variables of the $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ collection.

Example

(\begin{matrix} 〈3, 3, 8, 6〉, \\ 〈\begin{matrix} 𝚟𝚊𝚕 - 3 & 𝚗𝚘𝚌𝚌𝚞𝚛𝚛𝚎𝚗𝚌𝚎 - 2, \\ 𝚟𝚊𝚕 - 5 & 𝚗𝚘𝚌𝚌𝚞𝚛𝚛𝚎𝚗𝚌𝚎 - 0, \\ 𝚟𝚊𝚕 - 6 & 𝚗𝚘𝚌𝚌𝚞𝚛𝚛𝚎𝚗𝚌𝚎 - 1 \end{matrix}〉 \end{matrix})

The $𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢$ constraint holds since values 3, 5 and 6 respectively occur 2, 0 and 1 times within the collection $〈 3, 3, 8, 6 〉$ and since no restriction was specified for value 8.

All solutions

Figure 5.163.1 gives all solutions to the following non ground instance of the $𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢$ constraint: $V_{1} \in [3, 4]$ , $V_{2} \in [2, 3]$ , $V_{3} \in [1, 2]$ , $V_{4} \in [2, 4]$ , $V_{5} \in [2, 3]$ , $V_{6} \in [1, 2]$ , $O_{1} \in [1, 1]$ , $O_{2} \in [2, 3]$ , $O_{3} \in [0, 1]$ , $O_{4} \in [2, 3]$ , $𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢$ $(〈 V_{1}, V_{2}, V_{3}, V_{4}, V_{5}, V_{6} 〉, 〈 1 O_{1}, 2 O_{2}, 3 O_{3}, 4 O_{4} 〉)$ .

Figure 5.163.1. All solutions corresponding to the non ground example of the $𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢$ constraint of the All solutions slot

Typical

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | > 1

𝚛𝚊𝚗𝚐𝚎

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛) > 1

| 𝚅𝙰𝙻𝚄𝙴𝚂 | > 1

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | \geq | 𝚅𝙰𝙻𝚄𝙴𝚂 |

𝚖𝚒𝚗𝚟𝚊𝚕

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛) = 0 \lor

𝚒𝚗_𝚊𝚝𝚝𝚛

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚟𝚊𝚛, 𝚅𝙰𝙻𝚄𝙴𝚂, 𝚟𝚊𝚕)

Symmetries

Items of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ are permutable.
Items of $𝚅𝙰𝙻𝚄𝙴𝚂$ are permutable.
An occurrence of a value of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛$ that does not belong to $𝚅𝙰𝙻𝚄𝙴𝚂 . 𝚟𝚊𝚕$ can be replaced by any other value that also does not belong to $𝚅𝙰𝙻𝚄𝙴𝚂 . 𝚟𝚊𝚕$ .
All occurrences of two distinct values in $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛$ or $𝚅𝙰𝙻𝚄𝙴𝚂 . 𝚟𝚊𝚕$ can be swapped; all occurrences of a value in $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛$ or $𝚅𝙰𝙻𝚄𝙴𝚂 . 𝚟𝚊𝚕$ can be renamed to any unused value.

Arg. properties

Functional dependency: $𝚅𝙰𝙻𝚄𝙴𝚂 . 𝚗𝚘𝚌𝚌𝚞𝚛𝚛𝚎𝚗𝚌𝚎$ determined by $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ and $𝚅𝙰𝙻𝚄𝙴𝚂 . 𝚟𝚊𝚕$ .
Contractible wrt. $𝚅𝙰𝙻𝚄𝙴𝚂$ .

Usage

We show how to use the $𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢$ constraint in order to model the magic series problem [VanHentenryck89] with a single $𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢$ constraint. A non-empty finite series $S = (s_{0}, s_{1}, \dots, s_{n})$ is magic if and only if there are $s_{i}$ occurrences of $i$ in $S$ for each integer $i$ ranging from 0 to $n$ . This leads to the following model:

𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢 (\begin{matrix} 〈\begin{matrix} 𝚟𝚊𝚛 - s_{0}, 𝚟𝚊𝚛 - s_{1}, \dots, 𝚟𝚊𝚛 - s_{n} \end{matrix}〉, \\ 〈\begin{matrix} 𝚟𝚊𝚕 - 0 & 𝚗𝚘𝚌𝚌𝚞𝚛𝚛𝚎𝚗𝚌𝚎 - s_{0}, \\ 𝚟𝚊𝚕 - 1 & 𝚗𝚘𝚌𝚌𝚞𝚛𝚛𝚎𝚗𝚌𝚎 - s_{1}, \\ ⋮ \\ 𝚟𝚊𝚕 - n & 𝚗𝚘𝚌𝚌𝚞𝚛𝚛𝚎𝚗𝚌𝚎 - s_{n} \end{matrix}〉 \end{matrix})

Remark

This is a generalised form of the original $𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢$ constraint: in the original $𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢$ constraint [Regin96], one specifies for each value its minimum and maximum number of occurrences (i.e., see $𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢_𝚕𝚘𝚠_𝚞𝚙$ ). Here we give for each value $v$ a domain variable that indicates how many time value $v$ is actually used. By setting the minimum and maximum values of this variable to the appropriate constants we can express the same thing as in the original $𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢$ constraint. However, as shown in the magic series problem, we can also use this variable in other constraints. By reduction from 3-SAT, Claude-Guy Quimper shows in [Quimper03] that it is NP-hard to achieve arc-consistency for the count variables.

A last difference with the original $𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢$ constraint comes from the fact that there is no constraint on the values that are not explicitly mentioned in the $𝚅𝙰𝙻𝚄𝙴𝚂$ collection. In the original $𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢$ these values could not be assigned to the variables of the $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ collection. However allowing values that are not mentioned in $𝚅𝙰𝙻𝚄𝙴𝚂$ to be assigned to variables of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ can potentially avoid mentioning a huge number of unconstrained values in the $𝚅𝙰𝙻𝚄𝙴𝚂$ collection, and as a side effect, prevent possiblyOf course one could also, while generating a flow model, detect all unconstrained values in order to generate a single vertex in the flow model for the set of unconstrained values. generating a dense graph (i.e., see DFS-bottleneck) for the corresponding underlying flow model).

Within [BourdaisGalinierPesant03] the $𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢$ constraint is called $𝚍𝚒𝚜𝚝𝚛𝚒𝚋𝚞𝚝𝚒𝚘𝚗$ . Within [ReginGomes04] the $𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢$ constraint is called $𝚌𝚊𝚛𝚍_𝚟𝚊𝚛_𝚐𝚌𝚌$ . Within [BessiereHebrardHnichWalsh04a] the $𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢$ constraint is called $𝚎𝚐𝚌𝚌$ or $𝚛𝚐𝚌𝚌$ . This later case corresponds to the fact that some variables are duplicated within the $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ collection.

The $𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢$ constraint can be seen as a system (i.e., a conjunction) of $𝚊𝚖𝚘𝚗𝚐$ constraints.

When all count variables (i.e., the variables $𝚅𝙰𝙻𝚄𝙴𝚂 [i] . 𝚗𝚘𝚌𝚌𝚞𝚛𝚛𝚎𝚗𝚌𝚎$ with $i \in [1, | 𝚅𝙰𝙻𝚄𝙴𝚂 |]$ ) do not occur in any other constraints of the problem, it may be operationally more efficient to replace the $𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢$ constraint by a $𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢_𝚕𝚘𝚠_𝚞𝚙$ constraint where each count variable $𝚅𝙰𝙻𝚄𝙴𝚂 [i] . 𝚗𝚘𝚌𝚌𝚞𝚛𝚛𝚎𝚗𝚌𝚎$ is replaced by the corresponding interval $[\underset{̲}{𝚅𝙰𝙻𝚄𝙴𝚂 [i] . 𝚗𝚘𝚌𝚌𝚞𝚛𝚛𝚎𝚗𝚌𝚎}, \bar{𝚅𝙰𝙻𝚄𝙴𝚂 [i] . 𝚗𝚘𝚌𝚌𝚞𝚛𝚛𝚎𝚗𝚌𝚎}]$ . This stands for two reasons:

First, by using a $𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢_𝚕𝚘𝚠_𝚞𝚙$ constraint rather than a $𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢$ constraint, we avoid the filtering algorithm related to the count variables.
Second, unlike the $𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢$ constraint where we need to fix all its variables to get entailment, the $𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢_𝚕𝚘𝚠_𝚞𝚙$ constraint can be entailed before all its variables get fixed. As a result, this potentially avoid unnecessary calls to its filtering algorithm.

When all values that can be assigned to the variables of the $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ collection occur in the $𝚟𝚊𝚕$ attribute of the $𝚅𝙰𝙻𝚄𝙴𝚂$ collection, two implicit necessary conditionsNote that such necessary conditions can be derived by assigning an integer weight to each value [Simonis13], e.g. 1 for the first condition, the value itself for the second condition. inferred by double counting with the $𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢$ constraint are depicted by the following expressions:

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | = \sum_{i = 1}^{| 𝚅𝙰𝙻𝚄𝙴𝚂 |} 𝚅𝙰𝙻𝚄𝙴𝚂 [i] . 𝚗𝚘𝚌𝚌𝚞𝚛𝚛𝚎𝚗𝚌𝚎

\sum_{i = 1}^{| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 |} 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [i] . 𝚟𝚊𝚛 = \sum_{i = 1}^{| 𝚅𝙰𝙻𝚄𝙴𝚂 |} 𝚅𝙰𝙻𝚄𝙴𝚂 [i] . 𝚟𝚊𝚕 \cdot 𝚅𝙰𝙻𝚄𝙴𝚂 [i] . 𝚗𝚘𝚌𝚌𝚞𝚛𝚛𝚎𝚗𝚌𝚎

Within [Pitrat08] the previous condition where terms involving identical variables are grouped together (i.e., rule 5 of MALICE [Pitrat01]) is mentioned as a crucial deduction rule for the autoref problem.

W.-J. van Hoeve et al. present two soft versions of the $𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢$ constraint in [HoevePesantRousseau04].

In MiniZinc (http://www.minizinc.org/) there is also a $𝚍𝚒𝚜𝚝𝚛𝚒𝚋𝚞𝚝𝚎$ constraint where the $𝚟𝚊𝚕$ attribute is not necessarily initially fixed and where a same value may occur more than once. Their is also a $𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢_𝚌𝚕𝚘𝚜𝚎𝚍$ constraint where all variables must be assigned a value from the $𝚟𝚊𝚕$ attribute.

Algorithm

A flow algorithm that handles the original $𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢$ constraint is described in [Regin96]. The two approaches that were used to design bound-consistency algorithms for $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝$ were generalised for the $𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢$ constraint. The algorithm in [QuimperBeekOrtizGolynskiSadjad03] identifies Hall intervals and the one in [KatrielThiel03] exploits convexity to achieve a fast implementation of the flow-based arc-consistency algorithm. The later algorithm can also compute bound-consistency for the count variables [KatrielThielConstraints05], [Katriel05]. An improved algorithm for achieving arc-consistency is described in [QuimperLopezOrtizBeekGolynski04].

Systems

globalCardinality in Choco, count in Gecode, gcc in JaCoP, global_cardinality in MiniZinc, global_cardinality in SICStus.

$𝚘𝚙𝚎𝚗_𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢_𝚕𝚘𝚠_𝚞𝚙$ (assignment,counting constraint).

cost variant: $𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢_𝚠𝚒𝚝𝚑_𝚌𝚘𝚜𝚝𝚜$ ( $𝚌𝚘𝚜𝚝$ associated with each $𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎$ , $𝚟𝚊𝚕𝚞𝚎$ pair).

implied by: $𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢_𝚠𝚒𝚝𝚑_𝚌𝚘𝚜𝚝𝚜$ (forget about cost), $𝚜𝚊𝚖𝚎_𝚊𝚗𝚍_𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢$ (conjoin $𝚜𝚊𝚖𝚎$ and $𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢$ ).

part of system of constraints: $𝚊𝚖𝚘𝚗𝚐$ .

shift of concept: $𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢_𝚗𝚘_𝚕𝚘𝚘𝚙$ (assignment of a $𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎$ to its position is ignored), $𝚘𝚛𝚍𝚎𝚛𝚎𝚍_𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢$ (restrictions are done on nested sets of values, all starting from first value), $𝚜𝚢𝚖𝚖𝚎𝚝𝚛𝚒𝚌_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢$ , $𝚜𝚢𝚖𝚖𝚎𝚝𝚛𝚒𝚌_𝚐𝚌𝚌$ .

soft variant: $𝚘𝚙𝚎𝚗_𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢$ (a $𝚜𝚎𝚝$ $𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎$ defines the set of variables that are actually considered).

specialisation: $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝$ (each value should occur at most once), $𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢_𝚊𝚝𝚕𝚎𝚊𝚜𝚝$ , $𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢_𝚊𝚝𝚖𝚘𝚜𝚝$ (individual $𝚌𝚘𝚞𝚗𝚝 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎$ for each value replaced by single $𝚌𝚘𝚞𝚗𝚝 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎$ ), $𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢_𝚊𝚝𝚖𝚘𝚜𝚝_𝚙𝚊𝚛𝚝𝚒𝚝𝚒𝚘𝚗$ (individual $𝚌𝚘𝚞𝚗𝚝 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎$ for each value replaced by single $𝚌𝚘𝚞𝚗𝚝 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎$ and $𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎 \in 𝚙𝚊𝚛𝚝𝚒𝚝𝚒𝚘𝚗$ replaced by $𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎$ ), $𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢_𝚕𝚘𝚠_𝚞𝚙$ ( $𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎$ replaced by $𝚏𝚒𝚡𝚎𝚍$ $𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕$ ).

system of constraints: $𝚌𝚘𝚕𝚘𝚛𝚎𝚍_𝚖𝚊𝚝𝚛𝚒𝚡$ (one $𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢$ constraint for each $𝚛𝚘𝚠$ and each $𝚌𝚘𝚕𝚞𝚖𝚗$ of a $𝚖𝚊𝚝𝚛𝚒𝚡$ of $𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜$ ).

uses in its reformulation: $𝚝𝚛𝚎𝚎_𝚛𝚊𝚗𝚐𝚎$ , $𝚝𝚛𝚎𝚎_𝚛𝚎𝚜𝚘𝚞𝚛𝚌𝚎$ .

Keywords

application area: assignment.

characteristic of a constraint: core, automaton, automaton with array of counters.

complexity: 3-SAT.

constraint arguments: pure functional dependency.

constraint type: value constraint, counting constraint, system of constraints.

filtering: Hall interval, bound-consistency, flow, duplicated variables, DFS-bottleneck.

modelling: functional dependency.

modelling exercises: magic series.

puzzles: magic series, autoref.

Cond. implications

$•$ $𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚅𝙰𝙻𝚄𝙴𝚂)$

with $𝚖𝚒𝚗𝚟𝚊𝚕$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛) = 0$

implies $𝚊𝚗𝚍$ $(𝚅𝙰𝚁, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

when $𝚅𝙰𝚁 = 0$ .

$•$ $𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚅𝙰𝙻𝚄𝙴𝚂)$

with $𝚖𝚊𝚡𝚟𝚊𝚕$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛) = 1$

implies $𝚘𝚛$ $(𝚅𝙰𝚁, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

when $𝚅𝙰𝚁 = 1$ .

$•$ $𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚅𝙰𝙻𝚄𝙴𝚂)$

with $𝚖𝚒𝚗𝚟𝚊𝚕$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛) > 0$

implies $𝚖𝚒𝚗_𝚜𝚒𝚣𝚎_𝚏𝚞𝚕𝚕_𝚣𝚎𝚛𝚘_𝚜𝚝𝚛𝚎𝚝𝚌𝚑$ $(𝙼𝙸𝙽𝚂𝙸𝚉𝙴, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

when $𝙼𝙸𝙽𝚂𝙸𝚉𝙴 = | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 |$ .

$•$ $𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚅𝙰𝙻𝚄𝙴𝚂)$

with $𝚖𝚊𝚡𝚟𝚊𝚕$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛) < 0$

implies $𝚖𝚒𝚗_𝚜𝚒𝚣𝚎_𝚏𝚞𝚕𝚕_𝚣𝚎𝚛𝚘_𝚜𝚝𝚛𝚎𝚝𝚌𝚑$ $(𝙼𝙸𝙽𝚂𝙸𝚉𝙴, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

when $𝙼𝙸𝙽𝚂𝙸𝚉𝙴 = | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 |$ .

$•$ $𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚅𝙰𝙻𝚄𝙴𝚂)$

with $𝚛𝚊𝚗𝚐𝚎$ $(𝚅𝙰𝙻𝚄𝙴𝚂 . 𝚟𝚊𝚕) =$ $𝚗𝚟𝚊𝚕$ $(𝚅𝙰𝙻𝚄𝙴𝚂 . 𝚟𝚊𝚕)$

and $𝚖𝚒𝚗𝚟𝚊𝚕$ $(𝚅𝙰𝙻𝚄𝙴𝚂 . 𝚟𝚊𝚕) \leq$ $𝚖𝚒𝚗𝚟𝚊𝚕$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛)$

and $𝚖𝚊𝚡𝚟𝚊𝚕$ $(𝚅𝙰𝙻𝚄𝙴𝚂 . 𝚟𝚊𝚕) \geq$ $𝚖𝚊𝚡𝚟𝚊𝚕$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛)$

implies $𝚊𝚖𝚘𝚗𝚐_𝚍𝚒𝚏𝚏_0$ $(𝙽𝚅𝙰𝚁, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ .

$•$ $𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚅𝙰𝙻𝚄𝙴𝚂)$

with $𝚛𝚊𝚗𝚐𝚎$ $(𝚅𝙰𝙻𝚄𝙴𝚂 . 𝚟𝚊𝚕) =$ $𝚗𝚟𝚊𝚕$ $(𝚅𝙰𝙻𝚄𝙴𝚂 . 𝚟𝚊𝚕)$

and $𝚖𝚒𝚗𝚟𝚊𝚕$ $(𝚅𝙰𝙻𝚄𝙴𝚂 . 𝚟𝚊𝚕) \leq$ $𝚖𝚒𝚗𝚟𝚊𝚕$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛)$

and $𝚖𝚊𝚡𝚟𝚊𝚕$ $(𝚅𝙰𝙻𝚄𝙴𝚂 . 𝚟𝚊𝚕) \geq$ $𝚖𝚊𝚡𝚟𝚊𝚕$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛)$

implies $𝚊𝚝𝚖𝚘𝚜𝚝_𝚗𝚟𝚊𝚕𝚞𝚎$ $(𝙽𝚅𝙰𝙻, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ .

$•$ $𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚅𝙰𝙻𝚄𝙴𝚂)$

with $𝚛𝚊𝚗𝚐𝚎$ $(𝚅𝙰𝙻𝚄𝙴𝚂 . 𝚗𝚘𝚌𝚌𝚞𝚛𝚛𝚎𝚗𝚌𝚎) = 1$

and $𝚛𝚊𝚗𝚐𝚎$ $(𝚅𝙰𝙻𝚄𝙴𝚂 . 𝚟𝚊𝚕) =$ $𝚗𝚟𝚊𝚕$ $(𝚅𝙰𝙻𝚄𝙴𝚂 . 𝚟𝚊𝚕)$

and $𝚖𝚒𝚗𝚟𝚊𝚕$ $(𝚅𝙰𝙻𝚄𝙴𝚂 . 𝚟𝚊𝚕) =$ $𝚖𝚒𝚗𝚟𝚊𝚕$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛)$

and $𝚖𝚊𝚡𝚟𝚊𝚕$ $(𝚅𝙰𝙻𝚄𝙴𝚂 . 𝚟𝚊𝚕) =$ $𝚖𝚊𝚡𝚟𝚊𝚕$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛)$

implies $𝚋𝚊𝚕𝚊𝚗𝚌𝚎$ $(𝙱𝙰𝙻𝙰𝙽𝙲𝙴, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

when $𝙱𝙰𝙻𝙰𝙽𝙲𝙴 = 0$ .

$•$ $𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚅𝙰𝙻𝚄𝙴𝚂)$

with $𝚛𝚊𝚗𝚐𝚎$ $(𝚅𝙰𝙻𝚄𝙴𝚂 . 𝚟𝚊𝚕) =$ $𝚗𝚟𝚊𝚕$ $(𝚅𝙰𝙻𝚄𝙴𝚂 . 𝚟𝚊𝚕)$

and $𝚖𝚒𝚗𝚟𝚊𝚕$ $(𝚅𝙰𝙻𝚄𝙴𝚂 . 𝚟𝚊𝚕) \leq$ $𝚖𝚒𝚗𝚟𝚊𝚕$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛)$

and $𝚖𝚊𝚡𝚟𝚊𝚕$ $(𝚅𝙰𝙻𝚄𝙴𝚂 . 𝚟𝚊𝚕) \geq$ $𝚖𝚊𝚡𝚟𝚊𝚕$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛)$

implies $𝚖𝚊𝚡_𝚗$ $(𝙼𝙰𝚇, 𝚁𝙰𝙽𝙺, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ .

$•$ $𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚅𝙰𝙻𝚄𝙴𝚂)$

with $𝚛𝚊𝚗𝚐𝚎$ $(𝚅𝙰𝙻𝚄𝙴𝚂 . 𝚟𝚊𝚕) =$ $𝚗𝚟𝚊𝚕$ $(𝚅𝙰𝙻𝚄𝙴𝚂 . 𝚟𝚊𝚕)$

and $𝚖𝚒𝚗𝚟𝚊𝚕$ $(𝚅𝙰𝙻𝚄𝙴𝚂 . 𝚟𝚊𝚕) \leq$ $𝚖𝚒𝚗𝚟𝚊𝚕$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛)$

and $𝚖𝚊𝚡𝚟𝚊𝚕$ $(𝚅𝙰𝙻𝚄𝙴𝚂 . 𝚟𝚊𝚕) \geq$ $𝚖𝚊𝚡𝚟𝚊𝚕$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛)$

implies $𝚖𝚊𝚡_𝚗𝚟𝚊𝚕𝚞𝚎$ $(𝙼𝙰𝚇, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ .

$•$ $𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚅𝙰𝙻𝚄𝙴𝚂)$

with $𝚛𝚊𝚗𝚐𝚎$ $(𝚅𝙰𝙻𝚄𝙴𝚂 . 𝚟𝚊𝚕) =$ $𝚗𝚟𝚊𝚕$ $(𝚅𝙰𝙻𝚄𝙴𝚂 . 𝚟𝚊𝚕)$

and $𝚖𝚒𝚗𝚟𝚊𝚕$ $(𝚅𝙰𝙻𝚄𝙴𝚂 . 𝚟𝚊𝚕) \leq$ $𝚖𝚒𝚗𝚟𝚊𝚕$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛)$

and $𝚖𝚊𝚡𝚟𝚊𝚕$ $(𝚅𝙰𝙻𝚄𝙴𝚂 . 𝚟𝚊𝚕) \geq$ $𝚖𝚊𝚡𝚟𝚊𝚕$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛)$

implies $𝚖𝚒𝚗_𝚗$ $(𝙼𝙸𝙽, 𝚁𝙰𝙽𝙺, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ .

$•$ $𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚅𝙰𝙻𝚄𝙴𝚂)$

with $𝚛𝚊𝚗𝚐𝚎$ $(𝚅𝙰𝙻𝚄𝙴𝚂 . 𝚟𝚊𝚕) =$ $𝚗𝚟𝚊𝚕$ $(𝚅𝙰𝙻𝚄𝙴𝚂 . 𝚟𝚊𝚕)$

and $𝚖𝚒𝚗𝚟𝚊𝚕$ $(𝚅𝙰𝙻𝚄𝙴𝚂 . 𝚟𝚊𝚕) \leq$ $𝚖𝚒𝚗𝚟𝚊𝚕$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛)$

and $𝚖𝚊𝚡𝚟𝚊𝚕$ $(𝚅𝙰𝙻𝚄𝙴𝚂 . 𝚟𝚊𝚕) \geq$ $𝚖𝚊𝚡𝚟𝚊𝚕$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛)$

implies $𝚖𝚒𝚗_𝚗𝚟𝚊𝚕𝚞𝚎$ $(𝙼𝙸𝙽, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ .

$•$ $𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚅𝙰𝙻𝚄𝙴𝚂)$

with $𝚛𝚊𝚗𝚐𝚎$ $(𝚅𝙰𝙻𝚄𝙴𝚂 . 𝚟𝚊𝚕) =$ $𝚗𝚟𝚊𝚕$ $(𝚅𝙰𝙻𝚄𝙴𝚂 . 𝚟𝚊𝚕)$

and $𝚖𝚒𝚗𝚟𝚊𝚕$ $(𝚅𝙰𝙻𝚄𝙴𝚂 . 𝚟𝚊𝚕) \leq$ $𝚖𝚒𝚗𝚟𝚊𝚕$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛)$

and $𝚖𝚊𝚡𝚟𝚊𝚕$ $(𝚅𝙰𝙻𝚄𝙴𝚂 . 𝚟𝚊𝚕) \geq$ $𝚖𝚊𝚡𝚟𝚊𝚕$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛)$

implies $𝚛𝚊𝚗𝚐𝚎_𝚌𝚝𝚛$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝙲𝚃𝚁, 𝚁)$ .

For all items of $𝚅𝙰𝙻𝚄𝙴𝚂$ :

Arc input(s)

$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$

Arc generator

𝑆𝐸𝐿𝐹

\mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜)

Arc arity

Arc constraint(s)

𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 . 𝚟𝚊𝚛 = 𝚅𝙰𝙻𝚄𝙴𝚂 . 𝚟𝚊𝚕

Graph property(ies)

𝐍𝐕𝐄𝐑𝐓𝐄𝐗

= 𝚅𝙰𝙻𝚄𝙴𝚂 . 𝚗𝚘𝚌𝚌𝚞𝚛𝚛𝚎𝚗𝚌𝚎

Graph model

Since we want to express one unary constraint for each value we use the “For all items of $𝚅𝙰𝙻𝚄𝙴𝚂$ ” iterator. Part (A) of Figure 5.163.2 shows the initial graphs associated with each value 3, 5 and 6 of the $𝚅𝙰𝙻𝚄𝙴𝚂$ collection of the Example slot. Part (B) of Figure 5.163.2 shows the two corresponding final graphs respectively associated with values 3 and 6 that are both assigned to the variables of the $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ collection (since value 5 is not assigned to any variable of the $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ collection the final graph associated with value 5 is empty). Since we use the $𝐍𝐕𝐄𝐑𝐓𝐄𝐗$ graph property, the vertices of the final graphs are stressed in bold.

Figure 5.163.2. Initial and final graph of the $𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢$ constraint


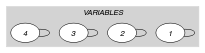
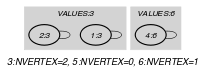
(a)	(b)

Automaton

Figure 5.163.3 depicts the automaton associated with the $𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢$ constraint. To each item of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ corresponds a signature variable $S_{i}$ that is equal to 0. To each item of the collection $𝚅𝙰𝙻𝚄𝙴𝚂$ corresponds a signature variable $S_{i + | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 |}$ that is equal to 1.

Figure 5.163.3. Automaton of the $𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢$ constraint

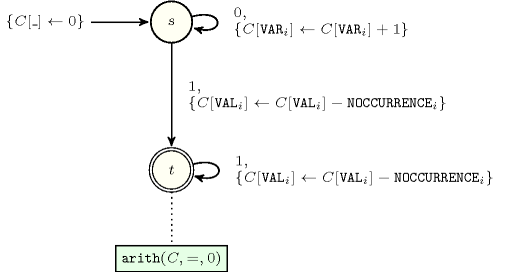
Quiz

$𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢$ : checking whether a ground instance holds or not ctrs/global_cardinality-3-tikz

$𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢$ : finding all solutions ctrs/global_cardinality-4-tikz

$𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢$ : identifying infeasible values ctrs/global_cardinality-5-tikz

$𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢$ : modelling a nurse assignment problem ctrs/global_cardinality-6-tikz

ctrs/global_cardinality-7-tikz

ctrs/global_cardinality-8-tikz

ctrs/global_cardinality-9-tikz

ctrs/global_cardinality-10-tikz

Global Constraint Catalog

5. Global Constraint Catalogue

5.163. global_cardinality

Figure 5.163.1. All solutions corresponding to the non ground example of the 𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢 constraint of the All solutions slot

Figure 5.163.2. Initial and final graph of the 𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢 constraint

Figure 5.163.3. Automaton of the 𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢 constraint

Figure 5.163.1. All solutions corresponding to the non ground example of the $𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢$ constraint of the All solutions slot

Figure 5.163.2. Initial and final graph of the $𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢$ constraint

Figure 5.163.3. Automaton of the $𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢$ constraint