5.71. clique
| DESCRIPTION | LINKS | GRAPH |
- Origin
- Constraint
- Arguments
- Restrictions
- Purpose
Consider a digraph described by the collection: to the item of the collection corresponds the vertex of ; To each value of the variable corresponds an arc from the vertex to the vertex. Select a subset of the vertices of that forms a clique of size (i.e., there is an arc between each pair of distinct vertices of ).
- Example
-
The constraint holds since the collection depicts a clique involving 3 vertices (namely vertices 2, 3 and 5) and since its first argument is set to the number of vertices of this clique.
- Typical
- Symmetry
Items of are permutable.
- Arg. properties
Functional dependency: determined by .
- Algorithm
[Fahle02], [Regin03CPAIOR], [Regin03]. The algorithm for finding maximum cliques in an undirected graph of C. Bron and J. Kerbosch [BronKerbosch73] was adapted by J.-C. Régin to the context of constraint programming in his papers.
- See also
common keyword: (constraint involving set variables, can be used for channelling).
- Keywords
constraint arguments: constraint involving set variables.
constraint type: graph constraint.
final graph structure: symmetric.
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
- Graph property(ies)
-
- Graph class
-
- Graph model
Note the use of set variables for modelling the fact that the vertices of the final graph have more than one successor: The successor variable associated with each vertex contains the successors of the corresponding vertex.
Part (A) of Figure 5.71.1 shows the initial graph from which we start. It is derived from the set associated with each vertex. Each set describes the potential values of the attribute of a given vertex. Part (B) of Figure 5.71.1 gives the final graph associated with the Example slot. Since we both use the and graph properties, the arcs and the vertices of the final graph are stressed in bold. The final graph corresponds to a clique containing three vertices.
Figure 5.71.1. Initial and final graph of the set constraint
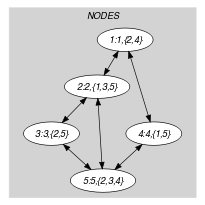
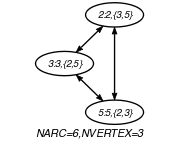
(a) (b)