5.190. increasing_sum
| DESCRIPTION | LINKS |
- Origin
- Constraint
- Synonyms
, .
- Arguments
- Restrictions
- Purpose
The variables of the collection are increasing. In addition, is the sum of the variables of the collection .
- Example
-
The constraint holds since:
The values of the collection are sorted in increasing order.
is set to the sum .
- Typical
- Arg. properties
Functional dependency: determined by .
- Usage
The constraint can be used for breaking some symmetries in bin packing problems. Given a set of bins with the same maximum capacity, and a set of items each of them with a specific height, the problem is to pack all items in the bins. To break symmetry we order bins by increasing use. This is done by introducing a variable for each bin giving its use, i.e., the sum of items heights assigned to bin , and by posting the following where denotes the sum of the heights of all the items to pack.
- Algorithm
A linear time filtering algorithm achieving bound-consistency for the constraint is described in [PetitReginBeldiceanu11]. This algorithm was motivated by the fact that achieving bound-consistency on the inequality constraints and on the sum constraint independently hinders propagation, as illustrated by the following small example, where the maximum value of is not reduced to 2: , , , , .
Given an constraint, the bound-consistency algorithm consists of three phases:
A normalisation phase adjusts the minimum and maximum value of variables with respect to the chain of inequalities . A forward phase adjusts the minimum value of (i.e., ), while a backward phase adjusts the maximum value of (i.e., ).
A phase restricts the minimum and maximum value of the sum variable with respect to the chain of inequalities (i.e., and ).
A final phase reduces the minimum and maximum value of variables both from the bounds of and from the chain of inequalities. Without loss of generality we now focus on the pruning of the maximum value of variables . For this purpose we first need to introduce the notion of last intersecting index of a variable , denoted by . This corresponds to the greatest index in such that , or if no such integer exists. Then the increase of the minimum value of when is equal to is equal to . When this increase exceeds the available margin, i.e. , we update the maximum value of .
We illustrate a part of the final phase on the following example , where , , , , , and . Observe that the domains are consistent with the first two phases of the algorithm, since,
the minimum (and maximum) values of variables are increasing,
the sum of the minimum of the variables , i.e., 28 is less than or equal to the maximum value of ,
the sum of the maximum of the variables , i.e., 45 is greater than or equal to the minimum value of .
Now, assume we want to know the increase of the minimum value of when is set to its maximum value 6. First we compute the last intersecting index of variable . Since is the last variable for which the minimum value is less than or equal to maximum value of we have . The increase is equal to . Since it exceeds the margin we have to reduce the maximum value of . How to do this incrementally is described in [PetitReginBeldiceanu11].
- Counting
-
Length () 2 3 4 5 6 7 8 Solutions 6 20 70 252 924 3432 12870 Number of solutions for : domains
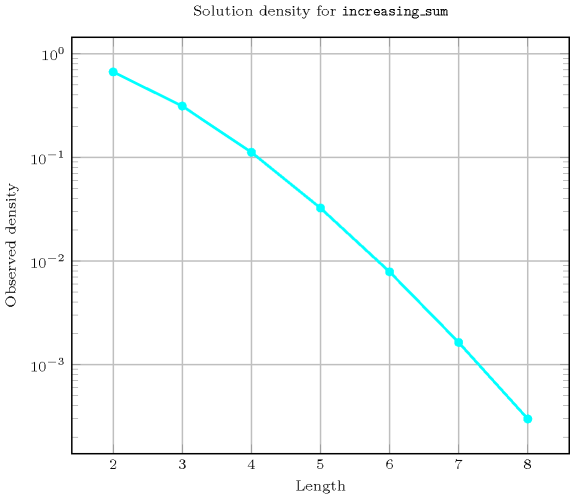
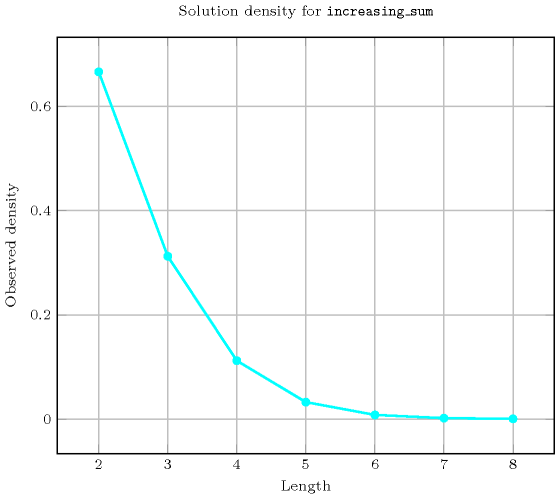
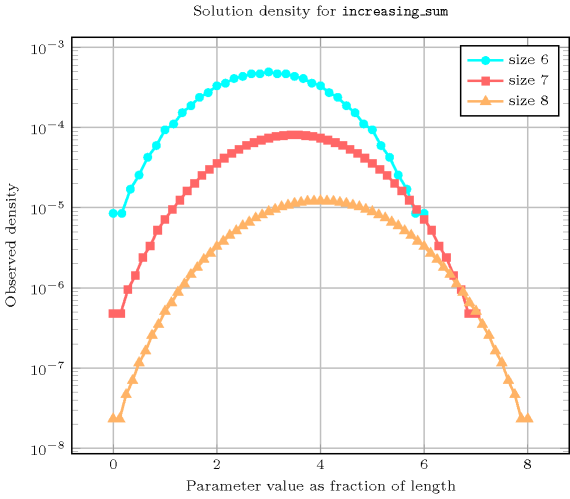
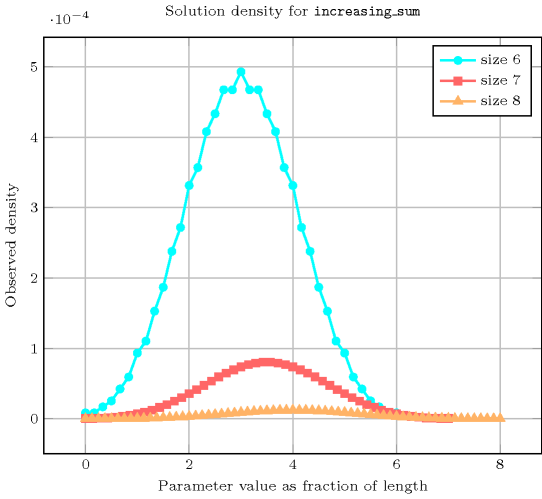
Length () 2 3 4 5 6 7 8 Total 6 20 70 252 924 3432 12870 Parameter value 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 3 1 3 3 3 3 3 3 4 1 3 5 5 5 5 5 5 - 3 5 7 7 7 7 6 - 3 7 9 11 11 11 7 - 2 7 11 13 15 15 8 - 1 8 14 18 20 22 9 - 1 7 16 22 26 28 10 - - 7 18 28 34 38 11 - - 5 19 32 42 48 12 - - 5 20 39 53 63 13 - - 3 20 42 63 77 14 - - 2 19 48 75 97 15 - - 1 18 51 87 116 16 - - 1 16 55 100 141 17 - - - 14 55 112 164 18 - - - 11 58 125 194 19 - - - 9 55 136 221 20 - - - 7 55 146 255 21 - - - 5 51 155 284 22 - - - 3 48 162 319 23 - - - 2 42 166 348 24 - - - 1 39 169 383 25 - - - 1 32 169 409 26 - - - - 28 166 440 27 - - - - 22 162 461 28 - - - - 18 155 486 29 - - - - 13 146 499 30 - - - - 11 136 515 31 - - - - 7 125 519 32 - - - - 5 112 526 33 - - - - 3 100 519 34 - - - - 2 87 515 35 - - - - 1 75 499 36 - - - - 1 63 486 37 - - - - - 53 461 38 - - - - - 42 440 39 - - - - - 34 409 40 - - - - - 26 383 41 - - - - - 20 348 42 - - - - - 15 319 43 - - - - - 11 284 44 - - - - - 7 255 45 - - - - - 5 221 46 - - - - - 3 194 47 - - - - - 2 164 48 - - - - - 1 141 49 - - - - - 1 116 50 - - - - - - 97 51 - - - - - - 77 52 - - - - - - 63 53 - - - - - - 48 54 - - - - - - 38 55 - - - - - - 28 56 - - - - - - 22 57 - - - - - - 15 58 - - - - - - 11 59 - - - - - - 7 60 - - - - - - 5 61 - - - - - - 3 62 - - - - - - 2 63 - - - - - - 1 64 - - - - - - 1 Solution count for : domains
- See also
-
implies: .
- Keywords
characteristic of a constraint: sum.
constraint type: predefined constraint, order constraint, arithmetic constraint.
- Cond. implications