Global Constraint Catalog: Call_min

5.11. all_min_dist

DESCRIPTION

LINKS

GRAPH

Origin

[Regin97]

Constraint

$𝚊𝚕𝚕_𝚖𝚒𝚗_𝚍𝚒𝚜𝚝 (𝙼𝙸𝙽𝙳𝙸𝚂𝚃, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

Synonyms

$𝚖𝚒𝚗𝚒𝚖𝚞𝚖_𝚍𝚒𝚜𝚝𝚊𝚗𝚌𝚎$ , $𝚒𝚗𝚝𝚎𝚛_𝚍𝚒𝚜𝚝𝚊𝚗𝚌𝚎$ .

Arguments

$𝙼𝙸𝙽𝙳𝙸𝚂𝚃$	$𝚒𝚗𝚝$
$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛)$

Restrictions

𝙼𝙸𝙽𝙳𝙸𝚂𝚃 > 0

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | < 2 \lor 𝙼𝙸𝙽𝙳𝙸𝚂𝚃 <

𝚛𝚊𝚗𝚐𝚎

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛)

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚟𝚊𝚛)

Purpose

Enforce for each pair $({𝚟𝚊𝚛}_{i}, {𝚟𝚊𝚛}_{j})$ of distinct variables of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ that $| {𝚟𝚊𝚛}_{i} - {𝚟𝚊𝚛}_{j} | \geq 𝙼𝙸𝙽𝙳𝙸𝚂𝚃$ .

Example

(2, 〈5, 1, 9, 3〉)

The $𝚊𝚕𝚕_𝚖𝚒𝚗_𝚍𝚒𝚜𝚝$ constraint holds since the following expressions $| 5 - 1 |$ , $| 5 - 9 |$ , $| 5 - 3 |$ , $| 1 - 9 |$ , $| 1 - 3 |$ , $| 9 - 3 |$ are all greater than or equal to the first argument $𝙼𝙸𝙽𝙳𝙸𝚂𝚃 = 2$ of the $𝚊𝚕𝚕_𝚖𝚒𝚗_𝚍𝚒𝚜𝚝$ constraint.

All solutions

Figure 5.11.1 gives all solutions to the following non ground instance of the $𝚊𝚕𝚕_𝚖𝚒𝚗_𝚍𝚒𝚜𝚝$ constraint: $V_{1} \in [0, 5]$ , $V_{2} \in [3, 9]$ , $V_{3} \in [5, 7]$ , $V_{4} \in [2, 10]$ , $𝚊𝚕𝚕_𝚖𝚒𝚗_𝚍𝚒𝚜𝚝$ $(3, 〈 V_{1}, V_{2}, V_{3}, V_{4} 〉)$ .

Figure 5.11.1. All solutions corresponding to the non ground example of the $𝚊𝚕𝚕_𝚖𝚒𝚗_𝚍𝚒𝚜𝚝$ constraint of the All solutions slot

Typical

𝙼𝙸𝙽𝙳𝙸𝚂𝚃 > 1

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | > 1

Symmetries

$𝙼𝙸𝙽𝙳𝙸𝚂𝚃$ can be decreased to any value $\geq 1$ .
Items of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ are permutable.
Two distinct values of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛$ can be swapped.
One and the same constant can be added to the $𝚟𝚊𝚛$ attribute of all items of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ .

Arg. properties

Contractible wrt. $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ .

Usage

The $𝚊𝚕𝚕_𝚖𝚒𝚗_𝚍𝚒𝚜𝚝$ constraint was initially created for handling frequency allocation problems. In [ArtiouchineBaptiste05] it is used for scheduling tasks that all have the same fixed duration in the context of air traffic management in the terminal radar control area of airports.

Remark

The $𝚊𝚕𝚕_𝚖𝚒𝚗_𝚍𝚒𝚜𝚝$ constraint can be modelled as a set of tasks that should not overlap. For each variable $𝚟𝚊𝚛$ of the $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ collection we create a task $t$ where $𝚟𝚊𝚛$ and $𝙼𝙸𝙽𝙳𝙸𝚂𝚃$ respectively correspond to the origin and the duration of $t$ .

Some solvers use in a pre-processing phase, while stating constraints of the form $| X_{i} - X_{j} | \geq D_{i j}$ (where $X_{i}$ and $X_{j}$ are domain variables and $D_{i j}$ is a constant), an algorithm for automatically extracting large cliques [BronKerbosch73] from such inequalities in order to state $𝚊𝚕𝚕_𝚖𝚒𝚗_𝚍𝚒𝚜𝚝$ constraints.

Algorithm

K. Artiouchine and P. Baptiste came up with a cubic time complexity algorithm achieving bound-consistency in [ArtiouchineBaptiste05], [ArtiouchineBaptiste07] based on the adaptation of a feasibility test algorithm from M.R. Garey et al. [GareyJohnsonSimonsTarjan81]. Later on, C.-G. Quimper et al., proposed a quadratic algorithm achieving the same level of consistency in [QuimperOrtizPesant06].

Counting

Length ( $n$ )	2	3	4	5	6	7	8
Solutions	8	24	120	720	5040	40320	362880

Number of solutions for $𝚊𝚕𝚕_𝚖𝚒𝚗_𝚍𝚒𝚜𝚝$ : domains $0 . . n$

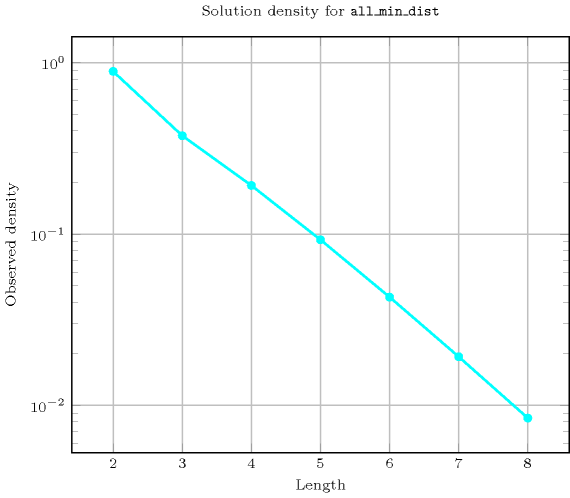
ctrs/all_min_dist-2-tikz

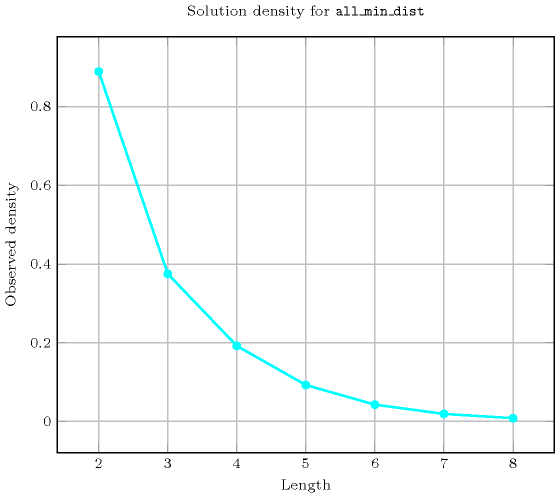
ctrs/all_min_dist-3-tikz

Length (

n

)

Total

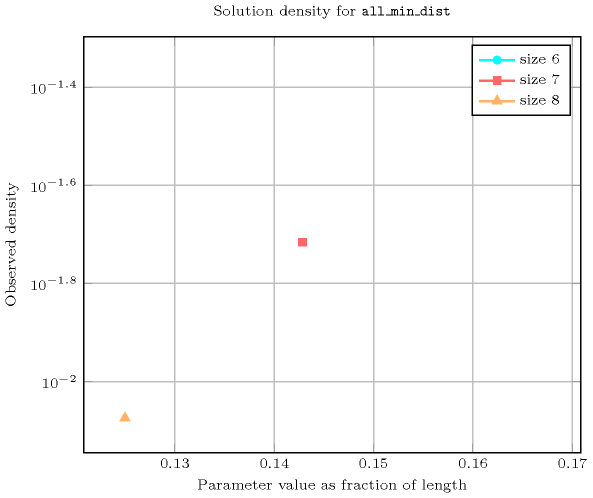
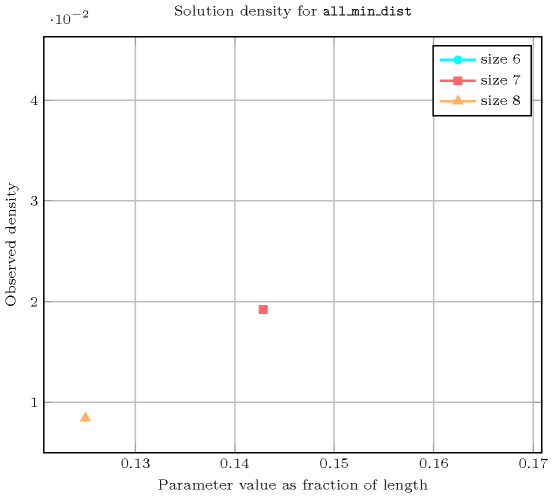
120

720

5040

40320

362880

Parameter

value

120

720

5040

40320

362880

Solution count for $𝚊𝚕𝚕_𝚖𝚒𝚗_𝚍𝚒𝚜𝚝$ : domains $0 . . n$

ctrs/all_min_dist-4-tikz

ctrs/all_min_dist-5-tikz

See also

generalisation: $𝚍𝚒𝚏𝚏𝚗$ ( $𝚕𝚒𝚗𝚎 𝚜𝚎𝚐𝚖𝚎𝚗𝚝$ , of same length, replaced by orthotope), $𝚍𝚒𝚜𝚓𝚞𝚗𝚌𝚝𝚒𝚟𝚎$ ( $𝚕𝚒𝚗𝚎 𝚜𝚎𝚐𝚖𝚎𝚗𝚝$ , of same length, replaced by $𝚕𝚒𝚗𝚎 𝚜𝚎𝚐𝚖𝚎𝚗𝚝$ ), $𝚖𝚞𝚕𝚝𝚒_𝚒𝚗𝚝𝚎𝚛_𝚍𝚒𝚜𝚝𝚊𝚗𝚌𝚎$ ( $𝙻𝙸𝙼𝙸𝚃$ parameter introduced to specify capacity $\geq$ 1).

implies: $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕$ , $𝚜𝚘𝚏𝚝_𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚟𝚊𝚛$ .

related: $𝚍𝚒𝚜𝚝𝚊𝚗𝚌𝚎$ .

specialisation: $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝$ ( $𝚕𝚒𝚗𝚎 𝚜𝚎𝚐𝚖𝚎𝚗𝚝$ , of same length, replaced by $𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎$ ).

Keywords

application area: frequency allocation problem, air traffic management.

characteristic of a constraint: sort based reformulation.

constraint type: value constraint, decomposition, scheduling constraint.

filtering: bound-consistency.

final graph structure: acyclic.

problems: maximum clique.

Cond. implications

$𝚊𝚕𝚕_𝚖𝚒𝚗_𝚍𝚒𝚜𝚝 (𝙼𝙸𝙽𝙳𝙸𝚂𝚃, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

implies $𝚜𝚘𝚏𝚝_𝚊𝚕𝚕_𝚎𝚚𝚞𝚊𝚕_𝚖𝚊𝚡_𝚟𝚊𝚛$ $(𝙽, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

when $𝙽 \geq | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | - 1$ .

Arc input(s)

$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$

Arc generator

𝐶𝐿𝐼𝑄𝑈𝐸

(<) \mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 1, 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 2)

Arc arity

Arc constraint(s)

𝚊𝚋𝚜 (𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 1 . 𝚟𝚊𝚛 - 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 2 . 𝚟𝚊𝚛) \geq 𝙼𝙸𝙽𝙳𝙸𝚂𝚃

Graph property(ies)

𝐍𝐀𝐑𝐂

= | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | * (| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | - 1) / 2

Graph class

•

𝙰𝙲𝚈𝙲𝙻𝙸𝙲

•

𝙽𝙾_𝙻𝙾𝙾𝙿

Graph model

We generate a clique with a minimum distance constraint between each pair of distinct vertices and state that the number of arcs of the final graph should be equal to the number of arcs of the initial graph.

Parts (A) and (B) of Figure 5.11.2 respectively show the initial and final graph associated with the Example slot. The $𝚊𝚕𝚕_𝚖𝚒𝚗_𝚍𝚒𝚜𝚝$ constraint holds since all the arcs of the initial graph belong to the final graph: all the minimum distance constraints are satisfied.

Figure 5.11.2. Initial and final graph of the $𝚊𝚕𝚕_𝚖𝚒𝚗_𝚍𝚒𝚜𝚝$ constraint


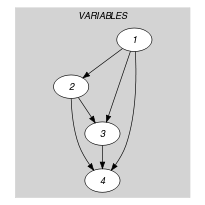
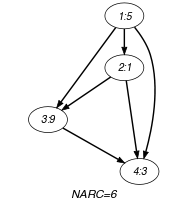
(a)	(b)

Global Constraint Catalog

5. Global Constraint Catalogue

5.11. all_min_dist

Figure 5.11.1. All solutions corresponding to the non ground example of the 𝚊𝚕𝚕_𝚖𝚒𝚗_𝚍𝚒𝚜𝚝 constraint of the All solutions slot

Figure 5.11.2. Initial and final graph of the 𝚊𝚕𝚕_𝚖𝚒𝚗_𝚍𝚒𝚜𝚝 constraint

Figure 5.11.1. All solutions corresponding to the non ground example of the $𝚊𝚕𝚕_𝚖𝚒𝚗_𝚍𝚒𝚜𝚝$ constraint of the All solutions slot

Figure 5.11.2. Initial and final graph of the $𝚊𝚕𝚕_𝚖𝚒𝚗_𝚍𝚒𝚜𝚝$ constraint