Global Constraint Catalog: Cincreasing_nvalue

5.188. increasing_nvalue_chain

DESCRIPTION

LINKS

GRAPH

AUTOMATON

Origin

Derived from $𝚒𝚗𝚌𝚛𝚎𝚊𝚜𝚒𝚗𝚐_𝚗𝚟𝚊𝚕𝚞𝚎$ .

Constraint

$𝚒𝚗𝚌𝚛𝚎𝚊𝚜𝚒𝚗𝚐_𝚗𝚟𝚊𝚕𝚞𝚎_𝚌𝚑𝚊𝚒𝚗 (𝙽𝚅𝙰𝙻, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

Arguments

$𝙽𝚅𝙰𝙻$	$𝚍𝚟𝚊𝚛$
$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚋 - 𝚍𝚟𝚊𝚛, 𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛)$

Restrictions

𝙽𝚅𝙰𝙻 \geq 𝚖𝚒𝚗 (1, | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 |)

𝙽𝚅𝙰𝙻 \leq | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 |

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, [𝚋, 𝚟𝚊𝚛])

𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚋 \geq 0

𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚋 \leq 1

Purpose

For each consecutive pair of items $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [i], 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [i + 1]$ $(1 \leq i < | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 |)$ of the $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ collection at least one of the following conditions hold:

$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [i + 1] . 𝚋 = 0$ ,
$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [i] . 𝚟𝚊𝚛 \leq 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [i + 1] . 𝚟𝚊𝚛$ .

In addition, $𝙽𝚅𝙰𝙻$ is equal to number of pairs of variables $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [i], 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [i + 1]$ $(1 \leq i < | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 |)$ plus one, which verify at least one of the following conditions:

$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [i + 1] . 𝚋 = 0$ ,
$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [i] . 𝚟𝚊𝚛 < 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [i + 1] . 𝚟𝚊𝚛$ .

Note that $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [1] . 𝚋$ is not referenced at all in the previous definition (i.e., its value does not influence at all the values assigned to the other variables).

Example

(\begin{matrix} 6, 〈\begin{matrix} 𝚋 - 0 & 𝚟𝚊𝚛 - 2, \\ 𝚋 - 1 & 𝚟𝚊𝚛 - 4, \\ 𝚋 - 1 & 𝚟𝚊𝚛 - 4, \\ 𝚋 - 1 & 𝚟𝚊𝚛 - 4, \\ 𝚋 - 0 & 𝚟𝚊𝚛 - 4, \\ 𝚋 - 1 & 𝚟𝚊𝚛 - 8, \\ 𝚋 - 0 & 𝚟𝚊𝚛 - 1, \\ 𝚋 - 0 & 𝚟𝚊𝚛 - 7, \\ 𝚋 - 1 & 𝚟𝚊𝚛 - 7 \end{matrix}〉 \end{matrix})

The $𝚒𝚗𝚌𝚛𝚎𝚊𝚜𝚒𝚗𝚐_𝚗𝚟𝚊𝚕𝚞𝚎_𝚌𝚑𝚊𝚒𝚗$ constraint holds since:

The condition $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [i + 1] . 𝚋 = 0 \lor 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [i] . 𝚟𝚊𝚛 \leq 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [i + 1] . 𝚟𝚊𝚛$ holds for every pair of adjacent items of the $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ collection:
- For the pair $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [1] . 𝚟𝚊𝚛, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [2] . 𝚟𝚊𝚛)$ we have $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [1] . 𝚟𝚊𝚛 \leq 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [2] . 𝚟𝚊𝚛$ $(2 \leq 4)$ .
- For the pair $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [2] . 𝚟𝚊𝚛, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [3] . 𝚟𝚊𝚛)$ we have $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [2] . 𝚟𝚊𝚛 \leq 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [3] . 𝚟𝚊𝚛$ $(4 \leq 4)$ .
- For the pair $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [3] . 𝚟𝚊𝚛, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [4] . 𝚟𝚊𝚛)$ we have $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [3] . 𝚟𝚊𝚛 \leq 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [4] . 𝚟𝚊𝚛$ $(4 \leq 4)$ .
- For the pair $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [4] . 𝚟𝚊𝚛, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [5] . 𝚟𝚊𝚛)$ we have $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [5] . 𝚋 = 0$ .
- For the pair $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [5] . 𝚟𝚊𝚛, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [6] . 𝚟𝚊𝚛)$ we have $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [5] . 𝚟𝚊𝚛 \leq 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [6] . 𝚟𝚊𝚛$ $(4 \leq 8)$ .
- For the pair $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [6] . 𝚟𝚊𝚛, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [7] . 𝚟𝚊𝚛)$ we have $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [7] . 𝚋 = 0$ .
- For the pair $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [7] . 𝚟𝚊𝚛, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [8] . 𝚟𝚊𝚛)$ we have $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [8] . 𝚋 = 0$ .
- For the pair $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [8] . 𝚟𝚊𝚛, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [9] . 𝚟𝚊𝚛)$ we have $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [8] . 𝚟𝚊𝚛 \leq 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [9] . 𝚟𝚊𝚛$ $(7 \leq 7)$ .
$𝙽𝚅𝙰𝙻$ is equal to number of pairs of variables $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [i], 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [i + 1]$ $(1 \leq i < | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 |)$ plus one which verify at least $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [i + 1] . 𝚋 = 0 \lor 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [i] . 𝚟𝚊𝚛 < 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [i + 1] . 𝚟𝚊𝚛$ . Beside the plus one, the following five pairs contribute for 1 in $𝙽𝚅𝙰𝙻$ :
- For the pair $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [1] . 𝚟𝚊𝚛, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [2] . 𝚟𝚊𝚛)$ we have $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [1] . 𝚟𝚊𝚛 \leq 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [2] . 𝚟𝚊𝚛$ $(2 < 4)$ .
- For the pair $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [4] . 𝚟𝚊𝚛, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [5] . 𝚟𝚊𝚛)$ we have $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [5] . 𝚋 = 0$ .
- For the pair $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [5] . 𝚟𝚊𝚛, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [6] . 𝚟𝚊𝚛)$ we have $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [5] . 𝚟𝚊𝚛 \leq 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [6] . 𝚟𝚊𝚛$ $(4 < 8)$ .
- For the pair $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [6] . 𝚟𝚊𝚛, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [7] . 𝚟𝚊𝚛)$ we have $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [7] . 𝚋 = 0$ .
- For the pair $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [7] . 𝚟𝚊𝚛, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [8] . 𝚟𝚊𝚛)$ we have $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [8] . 𝚋 = 0$ .

Typical

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | > 1

𝚛𝚊𝚗𝚐𝚎

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚋) > 1

𝚛𝚊𝚗𝚐𝚎

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛) > 1

Keywords

constraint type: counting constraint, order constraint.

modelling: number of distinct values.

Arc input(s)

$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$

Arc generator

𝑃𝐴𝑇𝐻

\mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 1, 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 2)

Arc arity

Arc constraint(s)

𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 2 . 𝚋 = 0 \lor 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 1 . 𝚟𝚊𝚛 \leq 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 2 . 𝚟𝚊𝚛

Graph property(ies)

𝐍𝐀𝐑𝐂

= | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | - 1

Arc input(s)

$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$

Arc generator

𝑃𝐴𝑇𝐻

\mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 1, 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 2)

Arc arity

Arc constraint(s)

𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 2 . 𝚋 = 0 \lor 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 1 . 𝚟𝚊𝚛 < 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 2 . 𝚟𝚊𝚛

Graph property(ies)

𝐍𝐀𝐑𝐂

= 𝙽𝚅𝙰𝙻 - 1

Graph model

Parts (A) and (B) of Figure 5.188.1 respectively show the initial and final graph associated with the second graph constraint of the Example slot. Since we use the $𝐍𝐀𝐑𝐂$ graph property the arcs of the final graph are stressed in bold.

Figure 5.188.1. Initial and final graph of the $𝚒𝚗𝚌𝚛𝚎𝚊𝚜𝚒𝚗𝚐_𝚗𝚟𝚊𝚕𝚞𝚎_𝚌𝚑𝚊𝚒𝚗$ constraint


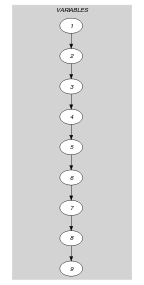
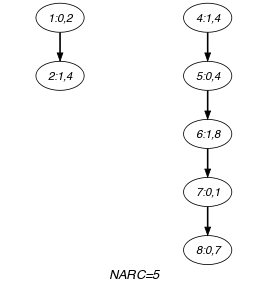
(a)	(b)

Automaton

Without loss of generality, assume that the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ contains at least one variable (i.e., $| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | \geq 1$ ). Let $l$ , $m$ , $n$ , $𝑚𝑖𝑛$ and $𝑚𝑎𝑥$ respectively denote the minimum and maximum possible value of variable $𝙽𝚅𝙰𝙻$ , the number of items of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ , the smallest value that can be assigned to $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [i] . 𝚟𝚊𝚛$ $(1 \leq i \leq n)$ , and the largest value that can be assigned to $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [i] . 𝚟𝚊𝚛$ $(1 \leq i \leq n)$ . Let $s = 𝑚𝑎𝑥 - 𝑚𝑖𝑛 + 1$ denote the total number of potential values. Clearly, the maximum value of $𝙽𝚅𝙰𝙻$ cannot exceed the quantity $d = min (m, n)$ . The states of the automaton that only accepts solutions of the $𝚒𝚗𝚌𝚛𝚎𝚊𝚜𝚒𝚗𝚐_𝚗𝚟𝚊𝚕𝚞𝚎_𝚌𝚑𝚊𝚒𝚗$ constraint can be defined in the following way:

We have an initial state labelled by $s_{00}$ .
We have $d \cdot s$ states labelled by $s_{i j}$ $(1 \leq i \leq d, 1 \leq j \leq s)$ .

Terminal states depend on the possible values of variable $𝙽𝚅𝙰𝙻$ and correspond to those states $s_{i j}$ such that $i$ is a possible value for variable $𝙽𝚅𝙰𝙻$ . Note that we assume no further restriction on the domain of $𝙽𝚅𝙰𝙻$ (otherwise the set of accepting states needs to be reduced in order to reflect the current set of possible values of $𝙽𝚅𝙰𝙻$ ).

Transitions of the automaton are labelled by a pair of values $(α, β)$ and correspond to a condition of the form $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [i] . 𝚋 = α \land 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [i] . 𝚟𝚊𝚛 = β$ , $(1 \leq i \leq n)$ . Characters $*$ and $+$ respectively represent all values in ${0, 1}$ and all values in ${𝑚𝑖𝑛, 𝑚𝑖𝑛 + 1, \dots, 𝑚𝑎𝑥}$ . Four classes of transitions are respectively defined in the following way:

There is a transition, labelled by the pair $(*, 𝑚𝑖𝑛 + j - 1)$ , from the initial state $s_{00}$ to the state $s_{1 j}$ $(1 \leq j \leq s)$ . We use the $*$ character since $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 [1] . 𝚋$ is not use at all in the definition of the $𝚒𝚗𝚌𝚛𝚎𝚊𝚜𝚒𝚗𝚐_𝚗𝚟𝚊𝚕𝚞𝚎_𝚌𝚑𝚊𝚒𝚗$ constraint.
There is a loop, labelled by the pair $(1, 𝑚𝑖𝑛 + j - 1)$ for every state $s_{i j}$ $(1 \leq i \leq d, 1 \leq j \leq s)$ .
$\forall i \in [1, d - 1], \forall j \in [1, s], \forall k \in [j + 1, s]$ there is a transition labelled by the pair $(1, 𝑚𝑖𝑛 + k - 1)$ from $s_{i j}$ to $s_{i + 1 k}$ .
$\forall i \in [1, d - 1], \forall j \in [1, s]$ there is a transition labelled by the pair $(0, +)$ from $s_{i j}$ to $s_{i + 11}$ .

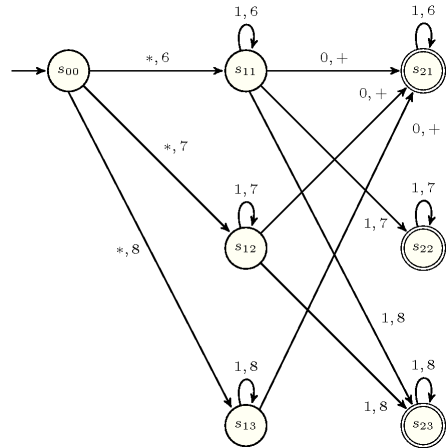
Figure 5.188.2. Automaton of the $𝚒𝚗𝚌𝚛𝚎𝚊𝚜𝚒𝚗𝚐_𝚗𝚟𝚊𝚕𝚞𝚎_𝚌𝚑𝚊𝚒𝚗$ constraint under the hypothesis that all variables are assigned a value in ${6, 7, 8}$ and that $𝙽𝚅𝙰𝙻$ is equal to 2. The character $*$ on a transition corresponds to a 0 or to a 1 and the $+$ corresponds to a 6, 7 or 8.

Global Constraint Catalog

5. Global Constraint Catalogue

5.188. increasing_nvalue_chain

Figure 5.188.1. Initial and final graph of the 𝚒𝚗𝚌𝚛𝚎𝚊𝚜𝚒𝚗𝚐_𝚗𝚟𝚊𝚕𝚞𝚎_𝚌𝚑𝚊𝚒𝚗 constraint

Figure 5.188.1. Initial and final graph of the $𝚒𝚗𝚌𝚛𝚎𝚊𝚜𝚒𝚗𝚐_𝚗𝚟𝚊𝚕𝚞𝚎_𝚌𝚑𝚊𝚒𝚗$ constraint