Global Constraint Catalog: Csum

5.383. sum

DESCRIPTION

LINKS

GRAPH

Origin

[Yunes02].

Constraint

$𝚜𝚞𝚖$ $(𝙸𝙽𝙳𝙴𝚇, 𝚂𝙴𝚃𝚂, 𝙲𝙾𝙽𝚂𝚃𝙰𝙽𝚃𝚂, 𝚂)$

Synonym

$𝚜𝚞𝚖_𝚙𝚛𝚎𝚍$ .

Arguments

$𝙸𝙽𝙳𝙴𝚇$	$𝚍𝚟𝚊𝚛$
$𝚂𝙴𝚃𝚂$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚒𝚗𝚍 - 𝚒𝚗𝚝, 𝚜𝚎𝚝 - 𝚜𝚒𝚗𝚝)$
$𝙲𝙾𝙽𝚂𝚃𝙰𝙽𝚃𝚂$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚌𝚜𝚝 - 𝚒𝚗𝚝)$
$𝚂$	$𝚍𝚟𝚊𝚛$

Restrictions

| 𝚂𝙴𝚃𝚂 | \geq 1

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚂𝙴𝚃𝚂, [𝚒𝚗𝚍, 𝚜𝚎𝚝])

𝚍𝚒𝚜𝚝𝚒𝚗𝚌𝚝

(𝚂𝙴𝚃𝚂, 𝚒𝚗𝚍)

| 𝙲𝙾𝙽𝚂𝚃𝙰𝙽𝚃𝚂 | \geq 1

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝙲𝙾𝙽𝚂𝚃𝙰𝙽𝚃𝚂, 𝚌𝚜𝚝)

Purpose

$𝚂$ is equal to the sum of the constants of $𝙲𝙾𝙽𝚂𝚃𝙰𝙽𝚃𝚂$ corresponding to the ${𝙸𝙽𝙳𝙴𝚇}^{t h}$ set of the $𝚂𝙴𝚃𝚂$ collection.

Example

(\begin{matrix} 8, 〈\begin{matrix} 𝚒𝚗𝚍 - 8 & 𝚜𝚎𝚝 - {2, 3}, \\ 𝚒𝚗𝚍 - 1 & 𝚜𝚎𝚝 - {3}, \\ 𝚒𝚗𝚍 - 3 & 𝚜𝚎𝚝 - {1, 4, 5}, \\ 𝚒𝚗𝚍 - 6 & 𝚜𝚎𝚝 - {2, 4} \end{matrix}〉, \\ 〈4, 9, 1, 3, 1〉, 10 \end{matrix})

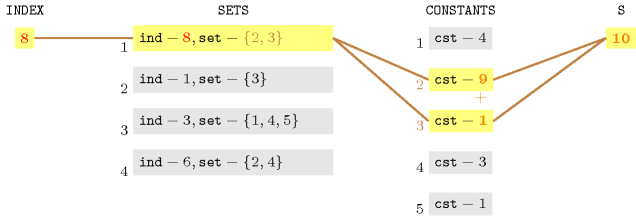
The $𝚜𝚞𝚖$ constraint holds since its last argument $𝚂 = 10$ is equal to the sum of the 2^th and 3^th items of the collection $〈 4, 9, 1, 3, 1 〉$ . As illustrated by Figure 5.383.1, this stems from the fact that its first argument $𝙸𝙽𝙳𝙴𝚇 = 8$ corresponds to the value of the $𝚒𝚗𝚍$ attribute of the first item of the $𝚂𝙴𝚃𝚂$ collection. Consequently the corresponding set ${2, 3}$ is used for summing the 2^th and 3^th items of the $𝙲𝙾𝙽𝚂𝚃𝙰𝙽𝚃𝚂$ collection.

Figure 5.383.1. Illustration of the correspondence between the arguments of the $𝚜𝚞𝚖$ $(𝙸𝙽𝙳𝙴𝚇, 𝚂𝙴𝚃𝚂, 𝙲𝙾𝙽𝚂𝚃𝙰𝙽𝚃𝚂, 𝚂)$ constraint in the context of the Example slot (from right to left, $𝚂 = 10$ is equal to the sum of the constants 9 and 1 corresponding to the indices 2 and 3 of the set for which the $𝚒𝚗𝚍$ attribute is equal to $𝙸𝙽𝙳𝙴𝚇 = 8$ )

Typical

| 𝚂𝙴𝚃𝚂 | > 1

| 𝙲𝙾𝙽𝚂𝚃𝙰𝙽𝚃𝚂 | > | 𝚂𝙴𝚃𝚂 |

𝚛𝚊𝚗𝚐𝚎

(𝙲𝙾𝙽𝚂𝚃𝙰𝙽𝚃𝚂 . 𝚌𝚜𝚝) > 1

Symmetry

Items of $𝚂𝙴𝚃𝚂$ are permutable.

Arg. properties

Functional dependency: $𝚂$ determined by $𝙸𝙽𝙳𝙴𝚇$ , $𝚂𝙴𝚃𝚂$ and $𝙲𝙾𝙽𝚂𝚃𝙰𝙽𝚃𝚂$ .

Usage

In his article introducing the $𝚜𝚞𝚖$ constraint, Tallys H. Yunes mentions the Sequence Dependent Cumulative Cost Problem as the subproblem that originally motivates this constraint.

Remark

The $𝚜𝚞𝚖$ constraint is called $𝚜𝚞𝚖_𝚙𝚛𝚎𝚍$ in MiniZinc (http://www.minizinc.org/).

Algorithm

The article [Yunes02] gives the convex hull relaxation of the $𝚜𝚞𝚖$ constraint.

Systems

sum_pred in MiniZinc.

used in graph description: $𝚒𝚗_𝚜𝚎𝚝$ .

Keywords

characteristic of a constraint: convex hull relaxation, sum.

constraint type: data constraint.

filtering: linear programming.

modelling: functional dependency.

Arc input(s)

$𝚂𝙴𝚃𝚂$ $𝙲𝙾𝙽𝚂𝚃𝙰𝙽𝚃𝚂$

Arc generator

𝑃𝑅𝑂𝐷𝑈𝐶𝑇

\mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚜𝚎𝚝𝚜, 𝚌𝚘𝚗𝚜𝚝𝚊𝚗𝚝𝚜)

Arc arity

Arc constraint(s)

• 𝙸𝙽𝙳𝙴𝚇 = 𝚜𝚎𝚝𝚜 . 𝚒𝚗𝚍

•

𝚒𝚗_𝚜𝚎𝚝

(𝚌𝚘𝚗𝚜𝚝𝚊𝚗𝚝𝚜 . 𝚔𝚎𝚢, 𝚜𝚎𝚝𝚜 . 𝚜𝚎𝚝)

Graph property(ies)

𝐒𝐔𝐌

(𝙲𝙾𝙽𝚂𝚃𝙰𝙽𝚃𝚂, 𝚌𝚜𝚝) = 𝚂

Graph model

According to the value assigned to $𝙸𝙽𝙳𝙴𝚇$ the arc constraint selects for the final graph:

The ${𝙸𝙽𝙳𝙴𝚇}^{t h}$ item of the $𝚂𝙴𝚃𝚂$ collection,
The items of the $𝙲𝙾𝙽𝚂𝚃𝙰𝙽𝚃𝚂$ collection for which the key correspond to the indices of the ${𝙸𝙽𝙳𝙴𝚇}^{t h}$ set of the $𝚂𝙴𝚃𝚂$ collection.

Finally, since we use the $𝐒𝐔𝐌$ graph property on the $𝚌𝚜𝚝$ attribute of the $𝙲𝙾𝙽𝚂𝚃𝙰𝙽𝚃𝚂$ collection, the last argument $𝚂$ of the $𝚜𝚞𝚖$ constraint is equal to the sum of the constants associated with the vertices of the final graph.

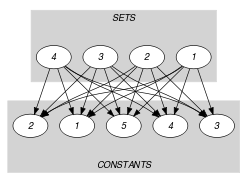
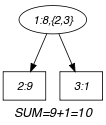
Parts (A) and (B) of Figure 5.383.2 respectively show the initial and final graph associated with the Example slot. Since we use the $𝐒𝐔𝐌$ graph property we show the vertices from which we compute $𝚂$ in a box.

Figure 5.383.2. Initial and final graph of the $𝚜𝚞𝚖$ constraint


(a)	(b)

Global Constraint Catalog

5. Global Constraint Catalogue

5.383. sum

Figure 5.383.2. Initial and final graph of the 𝚜𝚞𝚖 constraint

Figure 5.383.2. Initial and final graph of the $𝚜𝚞𝚖$ constraint