Global Constraint Catalog: Calldifferent_consecutive_values

5.14. alldifferent_consecutive_values

DESCRIPTION

LINKS

GRAPH

Origin

Derived from $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝$ .

Constraint

$𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚌𝚘𝚗𝚜𝚎𝚌𝚞𝚝𝚒𝚟𝚎_𝚟𝚊𝚕𝚞𝚎𝚜 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

Argument

𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂

𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛)

Restrictions

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚟𝚊𝚛)

𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)

Purpose

Enforce (1) all variables of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ to take distinct values and (2) constraint the difference between the largest and the smallest values of the $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ collection to be equal to the number of variables minus one (i.e., there is no holes at all within the used values).

Example

(〈5, 4, 3, 6〉)

The $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚌𝚘𝚗𝚜𝚎𝚌𝚞𝚝𝚒𝚟𝚎_𝚟𝚊𝚕𝚞𝚎𝚜$ constraint holds since (1) all the values 5, 4, 3 and 6 are distinct and since (2) all values between value 3 and value 6 are actually used.

All solutions

Figure 5.14.1 gives all solutions to the following non ground instance of the $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚌𝚘𝚗𝚜𝚎𝚌𝚞𝚝𝚒𝚟𝚎_𝚟𝚊𝚕𝚞𝚎𝚜$ constraint: $V_{1} \in {0, 1, 3, 4, 5, 6, 7, 8}$ , $V_{2} \in [4, 5]$ , $V_{3} \in [3, 4]$ , $V_{4} \in [0, 7]$ , $V_{5} \in [3, 4]$ , $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚌𝚘𝚗𝚜𝚎𝚌𝚞𝚝𝚒𝚟𝚎_𝚟𝚊𝚕𝚞𝚎𝚜$ $(〈 V_{1}, V_{2}, V_{3}, V_{4}, V_{5} 〉)$ .

Figure 5.14.1. All solutions corresponding to the non ground example of the $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚌𝚘𝚗𝚜𝚎𝚌𝚞𝚝𝚒𝚟𝚎_𝚟𝚊𝚕𝚞𝚎𝚜$ constraint of the All solutions slot

ctrs/alldifferent_consecutive_values-1-tikz

Typical

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | > 2

Symmetries

Items of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ are permutable.
Two distinct values of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛$ can be swapped.
One and the same constant can be added to the $𝚟𝚊𝚛$ attribute of all items of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ .

Counting

Length ( $n$ )	2	3	4	5	6	7	8	9	10
Solutions	4	12	48	240	1440	10080	80640	725760	7257600

Number of solutions for $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚌𝚘𝚗𝚜𝚎𝚌𝚞𝚝𝚒𝚟𝚎_𝚟𝚊𝚕𝚞𝚎𝚜$ : domains $0 . . n$

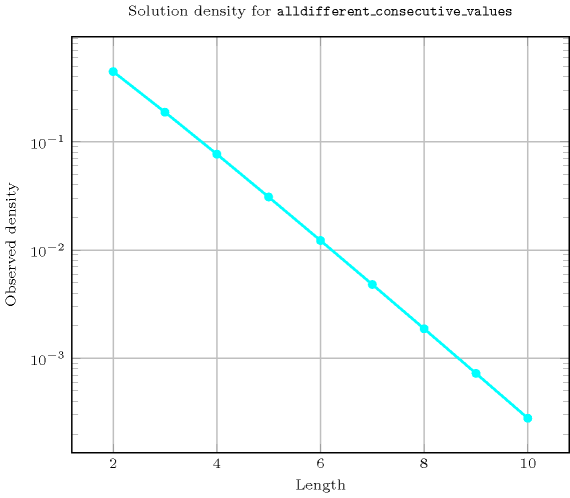
ctrs/alldifferent_consecutive_values-2-tikz

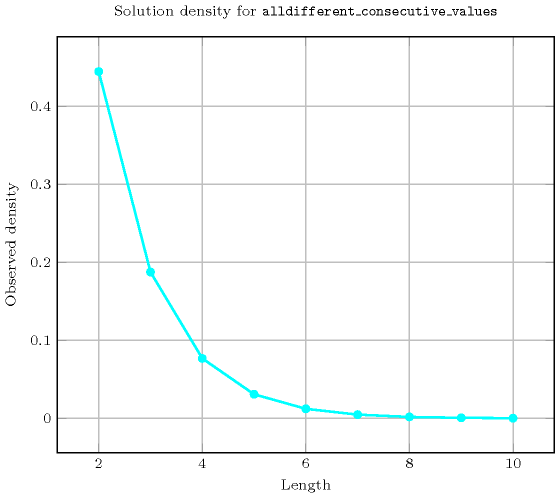
ctrs/alldifferent_consecutive_values-3-tikz

See also

implied by: $𝚙𝚎𝚛𝚖𝚞𝚝𝚊𝚝𝚒𝚘𝚗$ .

implies: $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝$ , $𝚌𝚘𝚗𝚜𝚎𝚌𝚞𝚝𝚒𝚟𝚎_𝚟𝚊𝚕𝚞𝚎𝚜$ .

Keywords

characteristic of a constraint: all different, disequality, sort based reformulation.

combinatorial object: permutation.

constraint type: value constraint.

Cond. implications

$•$ $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚌𝚘𝚗𝚜𝚎𝚌𝚞𝚝𝚒𝚟𝚎_𝚟𝚊𝚕𝚞𝚎𝚜 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

with $𝚖𝚒𝚗𝚟𝚊𝚕$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛) \leq 0$

and $𝚖𝚊𝚡𝚟𝚊𝚕$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛) \geq 0$

implies $𝚊𝚖𝚘𝚗𝚐_𝚍𝚒𝚏𝚏_0$ $(𝙽𝚅𝙰𝚁, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

when $𝙽𝚅𝙰𝚁 = | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | - 1$ .

$•$ $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚌𝚘𝚗𝚜𝚎𝚌𝚞𝚝𝚒𝚟𝚎_𝚟𝚊𝚕𝚞𝚎𝚜 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

with $𝚖𝚒𝚗𝚟𝚊𝚕$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛) > 0$

implies $𝚊𝚖𝚘𝚗𝚐_𝚍𝚒𝚏𝚏_0$ $(𝙽𝚅𝙰𝚁, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

when $𝙽𝚅𝙰𝚁 = | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 |$ .

$•$ $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚌𝚘𝚗𝚜𝚎𝚌𝚞𝚝𝚒𝚟𝚎_𝚟𝚊𝚕𝚞𝚎𝚜 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

with $𝚖𝚊𝚡𝚟𝚊𝚕$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛) < 0$

implies $𝚊𝚖𝚘𝚗𝚐_𝚍𝚒𝚏𝚏_0$ $(𝙽𝚅𝙰𝚁, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

when $𝙽𝚅𝙰𝚁 = | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 |$ .

$•$ $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚌𝚘𝚗𝚜𝚎𝚌𝚞𝚝𝚒𝚟𝚎_𝚟𝚊𝚕𝚞𝚎𝚜 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

implies $𝚋𝚊𝚕𝚊𝚗𝚌𝚎$ $(𝙱𝙰𝙻𝙰𝙽𝙲𝙴, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

when $𝙱𝙰𝙻𝙰𝙽𝙲𝙴 = 0$ .

$•$ $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚌𝚘𝚗𝚜𝚎𝚌𝚞𝚝𝚒𝚟𝚎_𝚟𝚊𝚕𝚞𝚎𝚜 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

with $| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | > 0$

implies $𝚕𝚎𝚗𝚐𝚝𝚑_𝚏𝚒𝚛𝚜𝚝_𝚜𝚎𝚚𝚞𝚎𝚗𝚌𝚎$ $(𝙻𝙴𝙽, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

when $𝙻𝙴𝙽 = 1$ .

$•$ $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚌𝚘𝚗𝚜𝚎𝚌𝚞𝚝𝚒𝚟𝚎_𝚟𝚊𝚕𝚞𝚎𝚜 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

with $| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | > 0$

implies $𝚕𝚎𝚗𝚐𝚝𝚑_𝚕𝚊𝚜𝚝_𝚜𝚎𝚚𝚞𝚎𝚗𝚌𝚎$ $(𝙻𝙴𝙽, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

when $𝙻𝙴𝙽 = 1$ .

$•$ $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚌𝚘𝚗𝚜𝚎𝚌𝚞𝚝𝚒𝚟𝚎_𝚟𝚊𝚕𝚞𝚎𝚜 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

implies $𝚖𝚊𝚡_𝚗$ $(𝙼𝙰𝚇, 𝚁𝙰𝙽𝙺, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

when $𝙼𝙰𝚇 =$ $𝚖𝚊𝚡𝚟𝚊𝚕$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛) - 𝚁𝙰𝙽𝙺$ .

$•$ $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚌𝚘𝚗𝚜𝚎𝚌𝚞𝚝𝚒𝚟𝚎_𝚟𝚊𝚕𝚞𝚎𝚜 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

implies $𝚖𝚒𝚗_𝚗$ $(𝙼𝙸𝙽, 𝚁𝙰𝙽𝙺, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

when $𝙼𝙸𝙽 =$ $𝚖𝚒𝚗𝚟𝚊𝚕$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛) + 𝚁𝙰𝙽𝙺$ .

$•$ $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚌𝚘𝚗𝚜𝚎𝚌𝚞𝚝𝚒𝚟𝚎_𝚟𝚊𝚕𝚞𝚎𝚜 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

with $| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | > 0$

implies $𝚖𝚒𝚗_𝚗𝚟𝚊𝚕𝚞𝚎$ $(𝙼𝙸𝙽, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

when $𝙼𝙸𝙽 = 1$ .

$•$ $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚌𝚘𝚗𝚜𝚎𝚌𝚞𝚝𝚒𝚟𝚎_𝚟𝚊𝚕𝚞𝚎𝚜 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

with $𝚖𝚒𝚗𝚟𝚊𝚕$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛) = 0$

implies $𝚗𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕$ $(𝙽𝚅𝙰𝙻, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻)$

when $𝙽𝚅𝙰𝙻 = (| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | + 𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻 - 1) / 𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻$ .

$•$ $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚌𝚘𝚗𝚜𝚎𝚌𝚞𝚝𝚒𝚟𝚎_𝚟𝚊𝚕𝚞𝚎𝚜 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

implies $𝚛𝚊𝚗𝚐𝚎_𝚌𝚝𝚛$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝙲𝚃𝚁, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

when $𝙲𝚃𝚁 \in [\leq]$

and $𝚁 = | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 |$ .

$•$ $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚌𝚘𝚗𝚜𝚎𝚌𝚞𝚝𝚒𝚟𝚎_𝚟𝚊𝚕𝚞𝚎𝚜 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

implies $𝚜𝚘𝚏𝚝_𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚌𝚝𝚛$ $(𝙲, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ .

Arc input(s): $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$
Arc generator: $𝑆𝐸𝐿𝐹$ $\mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜)$
Arc arity
Arc constraint(s): $𝚃𝚁𝚄𝙴$
Graph property(ies): $𝐑𝐀𝐍𝐆𝐄$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚟𝚊𝚛) = | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | - 1$