Global Constraint Catalog: Cchange

5.64. change_partition

DESCRIPTION

LINKS

GRAPH

Origin

Derived from $𝚌𝚑𝚊𝚗𝚐𝚎$ .

Constraint

$𝚌𝚑𝚊𝚗𝚐𝚎_𝚙𝚊𝚛𝚝𝚒𝚝𝚒𝚘𝚗 (𝙽𝙲𝙷𝙰𝙽𝙶𝙴, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝙿𝙰𝚁𝚃𝙸𝚃𝙸𝙾𝙽𝚂)$

Type

𝚅𝙰𝙻𝚄𝙴𝚂

𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚕 - 𝚒𝚗𝚝)

Arguments

$𝙽𝙲𝙷𝙰𝙽𝙶𝙴$	$𝚍𝚟𝚊𝚛$
$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛)$
$𝙿𝙰𝚁𝚃𝙸𝚃𝙸𝙾𝙽𝚂$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚙 - 𝚅𝙰𝙻𝚄𝙴𝚂)$

Restrictions

| 𝚅𝙰𝙻𝚄𝙴𝚂 | \geq 1

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝙻𝚄𝙴𝚂, 𝚟𝚊𝚕)

𝚍𝚒𝚜𝚝𝚒𝚗𝚌𝚝

(𝚅𝙰𝙻𝚄𝙴𝚂, 𝚟𝚊𝚕)

𝙽𝙲𝙷𝙰𝙽𝙶𝙴 \geq 0

𝙽𝙲𝙷𝙰𝙽𝙶𝙴 < | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 |

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚟𝚊𝚛)

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝙿𝙰𝚁𝚃𝙸𝚃𝙸𝙾𝙽𝚂, 𝚙)

| 𝙿𝙰𝚁𝚃𝙸𝚃𝙸𝙾𝙽𝚂 | \geq 2

Purpose

$𝙽𝙲𝙷𝙰𝙽𝙶𝙴$ is the number of times that the following constraint holds: $X$ and $Y$ do not belong to the same partition of the collection $𝙿𝙰𝚁𝚃𝙸𝚃𝙸𝙾𝙽𝚂$ , where $X$ and $Y$ correspond to consecutive variables of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ .

Example

(\begin{matrix} 2, 〈6, 6, 2, 1, 3, 3, 1, 6, 2, 2, 2〉, \\ 〈𝚙 - 〈1, 3〉, 𝚙 - 〈4〉, 𝚙 - 〈2, 6〉〉 \end{matrix})

In the example we have the following two changes:

One change between values 2 and 1 (since 2 and 1 respectively belong to the third and the first partition),
One change between values 1 and 6 (since 1 and 6 respectively belong to the first and the third partition).

Consequently the $𝚌𝚑𝚊𝚗𝚐𝚎_𝚙𝚊𝚛𝚝𝚒𝚝𝚒𝚘𝚗$ constraint holds since its first argument $𝙽𝙲𝙷𝙰𝙽𝙶𝙴$ is assigned to 2.

Typical

𝙽𝙲𝙷𝙰𝙽𝙶𝙴 > 0

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | > 1

𝚛𝚊𝚗𝚐𝚎

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛) > 1

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | > | 𝙿𝙰𝚁𝚃𝙸𝚃𝙸𝙾𝙽𝚂 |

Symmetries

Items of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ can be reversed.
Items of $𝙿𝙰𝚁𝚃𝙸𝚃𝙸𝙾𝙽𝚂$ are permutable.
Items of $𝙿𝙰𝚁𝚃𝙸𝚃𝙸𝙾𝙽𝚂 . 𝚙$ are permutable.
An occurrence of a value of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛$ can be replaced by any other value that also belongs to the same partition of $𝙿𝙰𝚁𝚃𝙸𝚃𝙸𝙾𝙽𝚂$ .

Arg. properties

Functional dependency: $𝙽𝙲𝙷𝙰𝙽𝙶𝙴$ determined by $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ and $𝙿𝙰𝚁𝚃𝙸𝚃𝙸𝙾𝙽𝚂$ .

Usage

This constraint is useful for the following problem: Assume you have to produce a set of orders, each order belonging to a given family. In the context of the Example slot we have three families that respectively correspond to values $1, 3$ , to value 4 and to values $2, 6$ . We would like to sequence the orders in such a way that we minimise the number of times two consecutive orders do not belong to the same family.

Algorithm

[BeldiceanuCarlsson01].

See also

common keyword: $𝚌𝚑𝚊𝚗𝚐𝚎$ (number of changes in a sequence of $𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜$ with respect to a $𝚋𝚒𝚗𝚊𝚛𝚢 𝚌𝚘𝚗𝚜𝚝𝚛𝚊𝚒𝚗𝚝$ ).

used in graph description: $𝚒𝚗_𝚜𝚊𝚖𝚎_𝚙𝚊𝚛𝚝𝚒𝚝𝚒𝚘𝚗$ .

Keywords

characteristic of a constraint: partition.

constraint arguments: pure functional dependency.

constraint type: timetabling constraint.

final graph structure: acyclic, bipartite, no loop.

modelling: number of changes, functional dependency.

Arc input(s)

$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$

Arc generator

𝑃𝐴𝑇𝐻

\mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 1, 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 2)

Arc arity

Arc constraint(s)

𝚒𝚗_𝚜𝚊𝚖𝚎_𝚙𝚊𝚛𝚝𝚒𝚝𝚒𝚘𝚗

(𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 1 . 𝚟𝚊𝚛, 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 2 . 𝚟𝚊𝚛, 𝙿𝙰𝚁𝚃𝙸𝚃𝙸𝙾𝙽𝚂)

Graph property(ies)

𝐍𝐀𝐑𝐂

= 𝙽𝙲𝙷𝙰𝙽𝙶𝙴

Graph class

•

𝙰𝙲𝚈𝙲𝙻𝙸𝙲

•

𝙱𝙸𝙿𝙰𝚁𝚃𝙸𝚃𝙴

•

𝙽𝙾_𝙻𝙾𝙾𝙿

Graph model

Parts (A) and (B) of Figure 5.64.1 respectively show the initial and final graph associated with the Example slot. Since we use the $𝐍𝐀𝐑𝐂$ graph property, the arcs of the final graph are stressed in bold.

Figure 5.64.1. Initial and final graph of the $𝚌𝚑𝚊𝚗𝚐𝚎_𝚙𝚊𝚛𝚝𝚒𝚝𝚒𝚘𝚗$ constraint


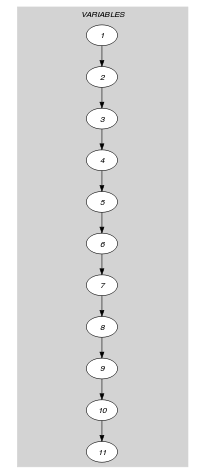
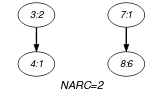
(a)	(b)

Global Constraint Catalog

5. Global Constraint Catalogue

5.64. change_partition

Figure 5.64.1. Initial and final graph of the 𝚌𝚑𝚊𝚗𝚐𝚎_𝚙𝚊𝚛𝚝𝚒𝚝𝚒𝚘𝚗 constraint

Figure 5.64.1. Initial and final graph of the $𝚌𝚑𝚊𝚗𝚐𝚎_𝚙𝚊𝚛𝚝𝚒𝚝𝚒𝚘𝚗$ constraint