Global Constraint Catalog: Call

5.5. all_equal

DESCRIPTION

LINKS

GRAPH

Origin

Derived from $𝚜𝚘𝚏𝚝_𝚊𝚕𝚕_𝚎𝚚𝚞𝚊𝚕_𝚖𝚒𝚗_𝚌𝚝𝚛$

Constraint

$𝚊𝚕𝚕_𝚎𝚚𝚞𝚊𝚕 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

Synonym

$𝚛𝚎𝚕$ .

Argument

𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂

𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛)

Restrictions

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚟𝚊𝚛)

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | > 0

Purpose

Enforce all variables of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ to take the same value.

Example

(〈5, 5, 5, 5〉)

The $𝚊𝚕𝚕_𝚎𝚚𝚞𝚊𝚕$ constraint holds since all its variables are fixed to value 5.

All solutions

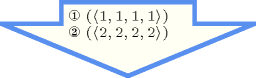
Figure 5.5.1 gives all solutions to the following non ground instance of the $𝚊𝚕𝚕_𝚎𝚚𝚞𝚊𝚕$ constraint: $V_{1} \in [0, 6]$ , $V_{2} \in [0, 2]$ , $V_{3} \in [0, 2]$ , $V_{4} \in [1, 4]$ , $𝚊𝚕𝚕_𝚎𝚚𝚞𝚊𝚕$ $(〈 V_{1}, V_{2}, V_{3}, V_{4} 〉)$ .

Figure 5.5.1. All solutions corresponding to the non ground example of the $𝚊𝚕𝚕_𝚎𝚚𝚞𝚊𝚕$ constraint of the All solutions slot

Typical

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | > 2

𝚖𝚒𝚗𝚟𝚊𝚕

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛) \neq 0

Symmetries

Items of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ are permutable.
All occurrences of a value of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛$ can be renamed to any unused value.

Arg. properties

Contractible wrt. $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ .

Counting

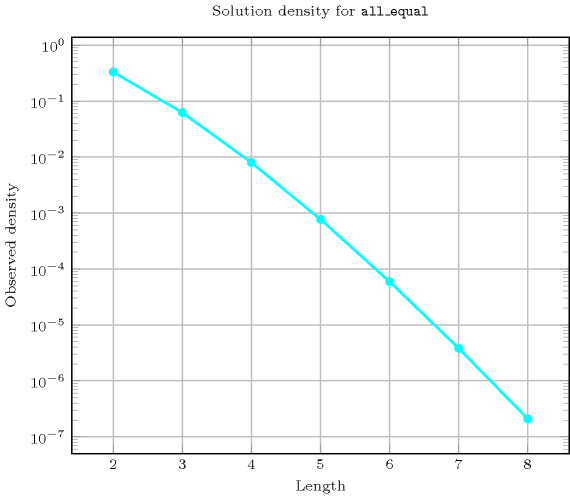
Length ( $n$ )	2	3	4	5	6	7	8
Solutions	3	4	5	6	7	8	9

Number of solutions for $𝚊𝚕𝚕_𝚎𝚚𝚞𝚊𝚕$ : domains $0 . . n$

ctrs/all_equal-2-tikz

ctrs/all_equal-3-tikz

Systems

atMostNValue in Choco, rel in Gecode, all_equal in MiniZinc.

See also

generalisation: $𝚗𝚟𝚊𝚕𝚞𝚎$ (a variable counting the number of distinct values is introduced).

implies: $𝚌𝚘𝚗𝚜𝚎𝚌𝚞𝚝𝚒𝚟𝚎_𝚟𝚊𝚕𝚞𝚎𝚜$ , $𝚍𝚎𝚌𝚛𝚎𝚊𝚜𝚒𝚗𝚐$ , $𝚒𝚗𝚌𝚛𝚎𝚊𝚜𝚒𝚗𝚐$ , $𝚖𝚞𝚕𝚝𝚒_𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚘𝚗𝚝𝚒𝚐𝚞𝚒𝚝𝚢$ .

negation: $𝚗𝚘𝚝_𝚊𝚕𝚕_𝚎𝚚𝚞𝚊𝚕$ .

soft variant: $𝚜𝚘𝚏𝚝_𝚊𝚕𝚕_𝚎𝚚𝚞𝚊𝚕_𝚖𝚊𝚡_𝚟𝚊𝚛$ ,

$𝚜𝚘𝚏𝚝_𝚊𝚕𝚕_𝚎𝚚𝚞𝚊𝚕_𝚖𝚒𝚗_𝚌𝚝𝚛$ (decomposition-based violation measure), $𝚜𝚘𝚏𝚝_𝚊𝚕𝚕_𝚎𝚚𝚞𝚊𝚕_𝚖𝚒𝚗_𝚟𝚊𝚛$ (variable-based violation measure).

specialisation: $𝚎𝚚$ (equality between just two variables).

Keywords

constraint type: value constraint.

Cond. implications

$𝚊𝚕𝚕_𝚎𝚚𝚞𝚊𝚕 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

with $| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | > 1$

implies $𝚜𝚘𝚖𝚎_𝚎𝚚𝚞𝚊𝚕$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ .

Arc input(s)

$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$

Arc generator

𝑃𝐴𝑇𝐻

\mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 1, 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 2)

Arc arity

Arc constraint(s)

𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 1 . 𝚟𝚊𝚛 = 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 2 . 𝚟𝚊𝚛

Graph property(ies)

𝐍𝐀𝐑𝐂

= | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | - 1

Graph model

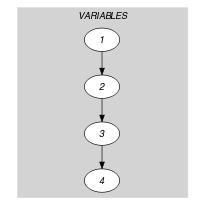
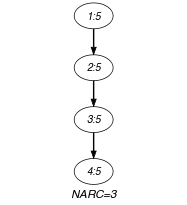
We use the arc generator $𝑃𝐴𝑇𝐻$ in order to link consecutive variables of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ by a binary equality constraint.

Parts (A) and (B) of Figure 5.5.2 respectively show the initial and final graph of the Example slot. Since we use the $𝐍𝐀𝐑𝐂$ graph property, the arcs of the final graph are stressed in bold.

Figure 5.5.2. Initial and final graph of the $𝚊𝚕𝚕_𝚎𝚚𝚞𝚊𝚕$ constraint


(a)	(b)

Global Constraint Catalog

5. Global Constraint Catalogue

5.5. all_equal

Figure 5.5.1. All solutions corresponding to the non ground example of the 𝚊𝚕𝚕_𝚎𝚚𝚞𝚊𝚕 constraint of the All solutions slot

Figure 5.5.2. Initial and final graph of the 𝚊𝚕𝚕_𝚎𝚚𝚞𝚊𝚕 constraint

Figure 5.5.1. All solutions corresponding to the non ground example of the $𝚊𝚕𝚕_𝚎𝚚𝚞𝚊𝚕$ constraint of the All solutions slot

Figure 5.5.2. Initial and final graph of the $𝚊𝚕𝚕_𝚎𝚚𝚞𝚊𝚕$ constraint