5.298. open_global_cardinality
| DESCRIPTION | LINKS | GRAPH |
- Origin
- Constraint
- Synonyms
, .
- Arguments
- Restrictions
- Purpose
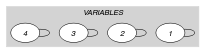
Each value should be taken by exactly variables of the collection for which the corresponding position belongs to the set . Positions are numbered from 1.
- Example
-
The constraint holds since:
Values 3, 5 and 6 respectively occur 1, 0 and 1 times within the collection (the first item 3 of is ignored since value 1 does not belong to the first argument of the constraint).
No constraint was specified for value 8.
- Typical
- Symmetries
Items of are permutable.
An occurrence of a value of that does not belong to can be replaced by any other value that also does not belong to .
- Usage
In their article [HoeveRegin06], W.-J. van Hoeve and J.-C. Régin motivate the constraint by the following scheduling problem. Consider a set of activities (where each activity has a fixed duration 1 and a start variable) that can be processed on two factory lines such that all the activities that will be processed on a given line must be pairwise distinct. This can be modelled by using one constraint for each line, involving all the start variables as well as a set variable whose final value specifies the set of activities assigned to that specific factory line.
Note that this can also be directly modelled by a single constraint. This is done by introducing an assignment variable for each activity. The initial domain of each assignment variable consists of two values that respectively correspond to the two factory lines.
- Remark
In their article [HoeveRegin06], W.-J. van Hoeve and J.-C. Régin consider the case where we have no counter variables for the values, but rather some lower and upper bounds (i.e., in fact the constraint).
- Algorithm
A slight adaptation of the flow model that handles the original constraint [Regin96] is described in [HoeveRegin06].
- See also
common keyword: (assignment,counting constraint), (open constraint,counting constraint),
, (open constraint,value constraint).
specialisation: (each active valueAn active value corresponds to a value occuring at a position mentionned in the set . should occur at most once), ( replaced by ).
- Keywords
-
constraint arguments: constraint involving set variables.
constraint type: open constraint, value constraint, counting constraint.
For all items of :
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
-
- Graph property(ies)
-
- Graph model
Since we want to express one unary constraint for each value we use the “For all items of ” iterator. The only difference with the graph model of the constraint is the arc constraint where we also specify that the position of the considered variable should belong to the first argument .
Part (A) of Figure 5.298.1 shows the initial graphs associated with each value 3, 5 and 6 of the collection of the Example slot. Part (B) of Figure 5.298.1 shows the two corresponding final graphs respectively associated with values 3 and 6 that are both assigned to those variables of the collection for which the index belongs to (since value 5 is not assigned to any variable of the collection the final graph associated with value 5 is empty). Since we use the graph property, the vertices of the final graphs are stressed in bold.
Figure 5.298.1. Initial and final graph of the constraint
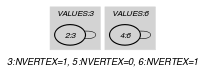
(a) (b)