5.20. alldifferent_partition
| DESCRIPTION | LINKS | GRAPH |
- Origin
- Constraint
- Synonyms
, .
- Type
- Arguments
- Restrictions
- Purpose
Enforce all variables of the collection to take values that belong to distinct partitions.
- Example
-
Since all variables take values that are located within distinct partitions the constraint holds.
- Typical
- Symmetries
Items of are permutable.
Items of are permutable.
Items of are permutable.
A value of can be renamed to any value that belongs to the same partition of .
Two distinct values of that do not belong to the same partition of can be swapped.
- Arg. properties
Contractible wrt. .
- See also
common keyword: Β (partition).
specialisation: Β ( replaced by ).
- Keywords
characteristic of a constraint: partition, all different, sort based reformulation.
constraint type: value constraint.
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
- Graph property(ies)
-
- Graph class
-
- Graph model
Similar to the constraint, but we replace the binary equality constraint of the constraint by the fact that two variables are respectively assigned to two values that belong to the same partition. We generate a clique with a constraint between each pair of vertices (including a vertex and itself) and state that the size of the largest strongly connected component should not exceed 1.
PartsΒ (A) andΒ (B) of FigureΒ 5.20.1 respectively show the initial and final graph associated with the Example slot. Since we use the graph property we show one of the largest strongly connected components of the final graph.
Figure 5.20.1. Initial and final graph of the constraint
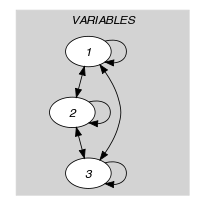
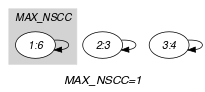
(a) (b)