- Origin
Derived from
- Constraint
-
- Synonym
.
- Argument
| |
- Restrictions
|
|
|
|
|
|
|
- Purpose
Enforce to cover a digraph described by
the collection with one circuit
visiting once a subset of the vertices of .
- Example
-
The constraint holds since its
argument depicts the following circuit visiting
successively the vertices 1, 2, 3 and 1
(i.e.,Β node 4 is not visited).
- Typical
-
- Symmetry
Items of are permutable.
- Counting
-
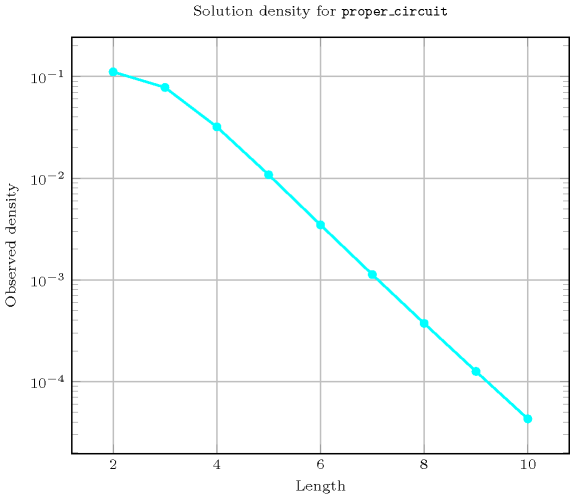
| Length () | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Solutions | 1 | 5 | 20 | 84 | 409 | 2365 | 16064 | 125664 | 1112073 |
Number of solutions for : domains
- See also
common keyword:
Β (permutation),
Β (permutation, one_succ),
Β (graph partitioning constraint, one_succ).
implied by:
.
implies:
,
.
implies (items to collection):
.
- Keywords
combinatorial object:
permutation.
constraint type:
graph constraint,
graph partitioning constraint.
filtering:
DFS-bottleneck.
final graph structure:
circuit,
one_succ.
