Global Constraint Catalog: Carith

5.32. arith_or

DESCRIPTION

LINKS

GRAPH

AUTOMATON

Origin

Used in the definition of several automata

Constraint

$𝚊𝚛𝚒𝚝𝚑_𝚘𝚛 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2, 𝚁𝙴𝙻𝙾𝙿, 𝚅𝙰𝙻𝚄𝙴)$

Arguments

$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛)$
$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛)$
$𝚁𝙴𝙻𝙾𝙿$	$𝚊𝚝𝚘𝚖$
$𝚅𝙰𝙻𝚄𝙴$	$𝚒𝚗𝚝$

Restrictions

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1, 𝚟𝚊𝚛)

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2, 𝚟𝚊𝚛)

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 | = | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 |

𝚁𝙴𝙻𝙾𝙿 \in [=, \neq, <, \geq, >, \leq]

Purpose

Enforce for all pairs of variables $𝚟𝚊𝚛 1_{i}, 𝚟𝚊𝚛 2_{i}$ of the $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ and $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ collections to have $𝚟𝚊𝚛 1_{i} 𝚁𝙴𝙻𝙾𝙿 𝚅𝙰𝙻𝚄𝙴 \lor 𝚟𝚊𝚛 2_{i} 𝚁𝙴𝙻𝙾𝙿 𝚅𝙰𝙻𝚄𝙴$ .

Example

(〈0, 1, 0, 0, 1〉, 〈0, 0, 0, 1, 0〉, =, 0)

The constraint $𝚊𝚛𝚒𝚝𝚑_𝚘𝚛$ holds since, for all pairs of variables $𝚟𝚊𝚛 1_{i}, 𝚟𝚊𝚛 2_{i}$ of the $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ and $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ collections, there is at least one variable that is equal to 0.

Typical

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 | > 0

𝚁𝙴𝙻𝙾𝙿 \in [=]

Symmetries

Arguments are permutable w.r.t. permutation $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2)$ $(𝚁𝙴𝙻𝙾𝙿)$ $(𝚅𝙰𝙻𝚄𝙴)$ .
Items of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ and $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ are permutable (same permutation used).

Arg. properties

Contractible wrt. $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ and $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ (remove items from same position).

See also

specialisation: $𝚊𝚛𝚒𝚝𝚑$ ( $𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎$ $𝚁𝙴𝙻𝙾𝙿$ $𝚅𝙰𝙻𝚄𝙴$ $\lor$ $𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎$ $𝚁𝙴𝙻𝙾𝙿$ $𝚅𝙰𝙻𝚄𝙴$ replaced by $𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎$ $𝚁𝙴𝙻𝙾𝙿$ $𝚅𝙰𝙻𝚄𝙴$ ).

Keywords

characteristic of a constraint: automaton, automaton without counters, reified automaton constraint.

constraint network structure: Berge-acyclic constraint network.

constraint type: decomposition, value constraint.

filtering: arc-consistency.

final graph structure: acyclic, bipartite, no loop.

modelling: disjunction.

Arc input(s)

$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$

Arc generator

𝑃𝑅𝑂𝐷𝑈𝐶𝑇

(=) \mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 1, 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 2)

Arc arity

Arc constraint(s)

𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 1 . 𝚟𝚊𝚛 𝚁𝙴𝙻𝙾𝙿 𝚅𝙰𝙻𝚄𝙴 \lor 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 2 . 𝚟𝚊𝚛 𝚁𝙴𝙻𝙾𝙿 𝚅𝙰𝙻𝚄𝙴

Graph property(ies)

𝐍𝐀𝐑𝐂

= | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 |

Graph class

•

𝙰𝙲𝚈𝙲𝙻𝙸𝙲

•

𝙱𝙸𝙿𝙰𝚁𝚃𝙸𝚃𝙴

•

𝙽𝙾_𝙻𝙾𝙾𝙿

Graph model

Parts (A) and (B) of Figure 5.32.1 respectively show the initial and final graphs associated with the Example slot. Since we use the $𝐍𝐀𝐑𝐂$ graph property, the arcs of the final graph are stressed in bold.

Figure 5.32.1. Initial and final graph of the $𝚊𝚛𝚒𝚝𝚑_𝚘𝚛$ constraint


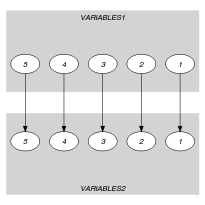
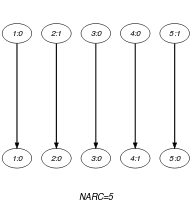
(a)	(b)

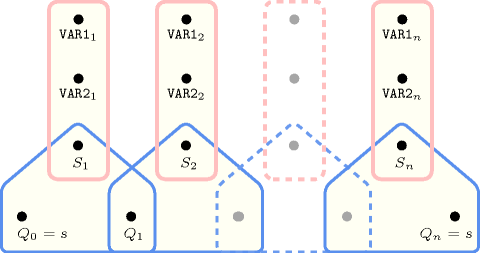
Automaton: Figure 5.32.2 depicts the automaton associated with the $𝚊𝚛𝚒𝚝𝚑_𝚘𝚛$ constraint. Let $𝚅𝙰𝚁 1_{i}$ and $𝚅𝙰𝚁 2_{i}$ be the $i^{t h}$ variables of the $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ and $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ collections. To each pair of variables $(𝚅𝙰𝚁 1_{i}, 𝚅𝙰𝚁 2_{i})$ corresponds a signature variable $S_{i}$ . The following signature constraint links $𝚅𝙰𝚁 1_{i}$ , $𝚅𝙰𝚁 2_{i}$ and $S_{i}$ : $𝚅𝙰𝚁 1_{i} 𝚁𝙴𝙻𝙾𝙿 𝚅𝙰𝙻𝚄𝙴 \lor 𝚅𝙰𝚁 2_{i} 𝚁𝙴𝙻𝙾𝙿 𝚅𝙰𝙻𝚄𝙴 \Leftrightarrow S_{i}$ . The automaton enforces for each pair of variables $𝚅𝙰𝚁 1_{i}$ , $𝚅𝙰𝚁 2_{i}$ the condition $𝚅𝙰𝚁 1_{i} 𝚁𝙴𝙻𝙾𝙿 𝚅𝙰𝙻𝚄𝙴 \lor 𝚅𝙰𝚁 2_{i} 𝚁𝙴𝙻𝙾𝙿 𝚅𝙰𝙻𝚄𝙴$ .

Figure 5.32.2. Automaton of the $𝚊𝚛𝚒𝚝𝚑_𝚘𝚛$ constraint

Figure 5.32.3. Hypergraph of the reformulation corresponding to the automaton of the $𝚊𝚛𝚒𝚝𝚑_𝚘𝚛$ constraint

Global Constraint Catalog

5. Global Constraint Catalogue

5.32. arith_or

Figure 5.32.1. Initial and final graph of the $𝚊𝚛𝚒𝚝𝚑_𝚘𝚛$ constraint

Figure 5.32.2. Automaton of the $𝚊𝚛𝚒𝚝𝚑_𝚘𝚛$ constraint

Figure 5.32.3. Hypergraph of the reformulation corresponding to the automaton of the $𝚊𝚛𝚒𝚝𝚑_𝚘𝚛$ constraint

Global Constraint Catalog

5. Global Constraint Catalogue

5.32. arith_or

Figure 5.32.1. Initial and final graph of the 𝚊𝚛𝚒𝚝𝚑_𝚘𝚛 constraint

Figure 5.32.2. Automaton of the 𝚊𝚛𝚒𝚝𝚑_𝚘𝚛 constraint

Figure 5.32.3. Hypergraph of the reformulation corresponding to the automaton of the 𝚊𝚛𝚒𝚝𝚑_𝚘𝚛 constraint

Figure 5.32.1. Initial and final graph of the $𝚊𝚛𝚒𝚝𝚑_𝚘𝚛$ constraint

Figure 5.32.2. Automaton of the $𝚊𝚛𝚒𝚝𝚑_𝚘𝚛$ constraint

Figure 5.32.3. Hypergraph of the reformulation corresponding to the automaton of the $𝚊𝚛𝚒𝚝𝚑_𝚘𝚛$ constraint