Global Constraint Catalog: Call_equal_peak

5.7. all_equal_peak_max

DESCRIPTION

LINKS

AUTOMATON

Origin

Derived from $𝚙𝚎𝚊𝚔$ and $𝚊𝚕𝚕_𝚎𝚚𝚞𝚊𝚕$ .

Constraint

$𝚊𝚕𝚕_𝚎𝚚𝚞𝚊𝚕_𝚙𝚎𝚊𝚔_𝚖𝚊𝚡 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

Argument

𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂

𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛)

Restrictions

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | > 0

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚟𝚊𝚛)

Purpose

A variable $V_{k}$ $(1 < k < m)$ of the sequence of variables $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 = V_{1}, \dots, V_{m}$ is a peak if and only if there exists an $i$ $(1 < i \leq k)$ such that $V_{i - 1} < V_{i}$ and $V_{i} = V_{i + 1} = \dots = V_{k}$ and $V_{k} > V_{k + 1}$ .

Enforce all the peaks of the sequence $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ to be assigned the same value, i.e. to be located at the same altitude corresponding to the maximum value of the sequence $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ .

Example

(〈1, 5, 5, 4, 3, 5, 2, 5〉)

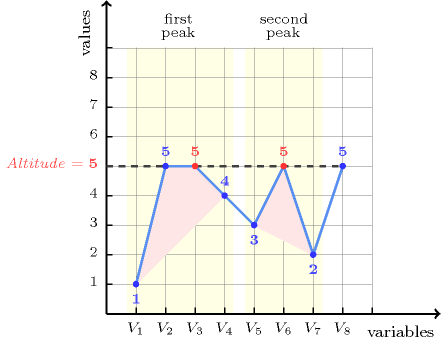
The $𝚊𝚕𝚕_𝚎𝚚𝚞𝚊𝚕_𝚙𝚎𝚊𝚔_𝚖𝚊𝚡$ constraint holds since the two peaks, in bold, of the sequence $15543525$ are located at the same altitude 5 that is also the maximum value of the sequence $15543525$ . Figure 5.7.1 depicts the solution associated with the example.

Figure 5.7.1. Illustration of the Example slot: a sequence of eight variables $V_{1}$ , $V_{2}$ , $V_{3}$ , $V_{4}$ , $V_{5}$ , $V_{6}$ , $V_{7}$ , $V_{8}$ respectively fixed to values 1, 5, 5, 4, 3, 5, 2, 5 and its corresponding two peaks, in red, both located at altitude 5 that also corresponds to the maximum value of the sequence

Note that the $𝚊𝚕𝚕_𝚎𝚚𝚞𝚊𝚕_𝚙𝚎𝚊𝚔_𝚖𝚊𝚡$ constraint does not enforce that the sequence $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ contains at least one peak.

Typical

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | \geq 5

𝚛𝚊𝚗𝚐𝚎

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛) > 1

𝚙𝚎𝚊𝚔

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛) \geq 2

Symmetries

Items of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ can be reversed.
One and the same constant can be added to the $𝚟𝚊𝚛$ attribute of all items of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ .

Arg. properties

Prefix-contractible wrt. $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ .
Suffix-contractible wrt. $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ .

Counting

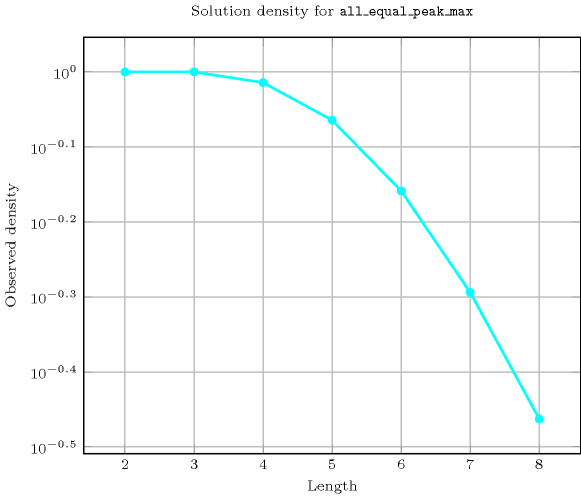
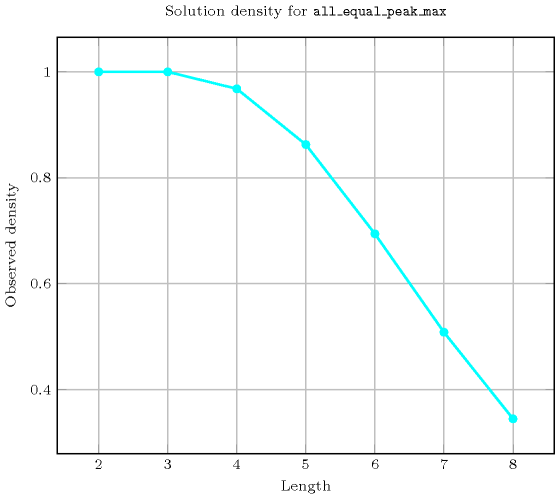
Length ( $n$ )	2	3	4	5	6	7	8
Solutions	9	64	605	6707	81648	1065542	14829903

Number of solutions for $𝚊𝚕𝚕_𝚎𝚚𝚞𝚊𝚕_𝚙𝚎𝚊𝚔_𝚖𝚊𝚡$ : domains $0 . . n$

ctrs/all_equal_peak_max-2-tikz

ctrs/all_equal_peak_max-3-tikz

See also

implied by: $𝚗𝚘_𝚙𝚎𝚊𝚔$ .

implies: $𝚊𝚕𝚕_𝚎𝚚𝚞𝚊𝚕_𝚙𝚎𝚊𝚔$ .

Keywords

characteristic of a constraint: automaton, automaton with counters, automaton with same input symbol.

combinatorial object: sequence.

constraint network structure: sliding cyclic(1) constraint network(2).

Cond. implications

$•$ $𝚊𝚕𝚕_𝚎𝚚𝚞𝚊𝚕_𝚙𝚎𝚊𝚔_𝚖𝚊𝚡 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

with $𝚙𝚎𝚊𝚔$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛) > 1$

implies $𝚜𝚘𝚖𝚎_𝚎𝚚𝚞𝚊𝚕$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ .

$•$ $𝚊𝚕𝚕_𝚎𝚚𝚞𝚊𝚕_𝚙𝚎𝚊𝚔_𝚖𝚊𝚡 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

with $𝚙𝚎𝚊𝚔$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛) > 0$

implies $𝚗𝚘𝚝_𝚊𝚕𝚕_𝚎𝚚𝚞𝚊𝚕$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ .

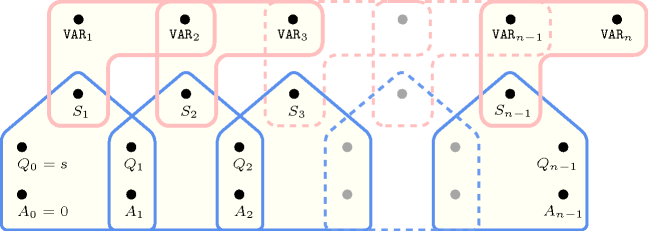
Automaton: Figure 5.7.2 depicts the automaton associated with the $𝚊𝚕𝚕_𝚎𝚚𝚞𝚊𝚕_𝚙𝚎𝚊𝚔_𝚖𝚊𝚡$ constraint. To each pair of consecutive variables $({𝚅𝙰𝚁}_{i}, {𝚅𝙰𝚁}_{i + 1})$ of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ corresponds a signature variable $S_{i}$ . The following signature constraint links ${𝚅𝙰𝚁}_{i}$ , ${𝚅𝙰𝚁}_{i + 1}$ and $S_{i}$ : $({𝚅𝙰𝚁}_{i} < {𝚅𝙰𝚁}_{i + 1} \Leftrightarrow S_{i} = 0) \land ({𝚅𝙰𝚁}_{i} = {𝚅𝙰𝚁}_{i + 1} \Leftrightarrow S_{i} = 1) \land ({𝚅𝙰𝚁}_{i} > {𝚅𝙰𝚁}_{i + 1} \Leftrightarrow S_{i} = 2)$ .

Figure 5.7.2. Automaton for the $𝚊𝚕𝚕_𝚎𝚚𝚞𝚊𝚕_𝚙𝚎𝚊𝚔_𝚖𝚊𝚡$ constraint; note the conditional transition from state $k$ to state $j$ testing that the counter $𝐴𝑙𝑡𝑖𝑡𝑢𝑑𝑒$ is equal to ${𝚅𝙰𝚁}_{i}$ for enforcing that all peaks are located at the same altitude; the conditional transitions from $j$ to $k$ and from $k$ to $k$ and the final check $𝐴𝑙𝑡𝑖𝑡𝑢𝑑𝑒 \geq {𝚅𝙰𝚁}_{| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 |}$ enforce the maximum value of the sequence $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ to not exceed the altitude of the eventual peaks.

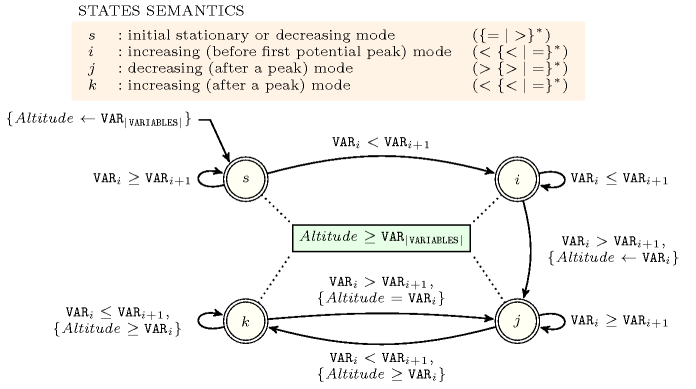
Figure 5.7.3. Hypergraph of the reformulation corresponding to the automaton of the $𝚊𝚕𝚕_𝚎𝚚𝚞𝚊𝚕_𝚙𝚎𝚊𝚔_𝚖𝚊𝚡$ constraint where $A$ stands for the value of the counter $𝐴𝑙𝑡𝑖𝑡𝑢𝑑𝑒$ (since all states of the automaton are accepting there is no restriction on the last variable $Q_{n - 1}$ )

Global Constraint Catalog

5. Global Constraint Catalogue

5.7. all_equal_peak_max