Global Constraint Catalog: Calldifferent

5.17. alldifferent_interval

DESCRIPTION

LINKS

GRAPH

AUTOMATON

Origin

Derived from $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝$ .

Constraint

$𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻)$

Synonyms

$𝚊𝚕𝚕𝚍𝚒𝚏𝚏_𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕$ , $𝚊𝚕𝚕𝚍𝚒𝚜𝚝𝚒𝚗𝚌𝚝_𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕$ .

Arguments

$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛)$
$𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻$	$𝚒𝚗𝚝$

Restrictions

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚟𝚊𝚛)

𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻 > 0

Purpose

Enforce all variables of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ to belong to distinct intervals. The intervals are defined by $[𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻 \cdot k, 𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻 \cdot k + 𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻 - 1]$ where $k$ is an integer.

Example

(〈2, 4, 10〉, 3)

In the example, the second argument $𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻 = 3$ defines the following family of intervals $[3 \cdot k, 3 \cdot k + 2]$ , where $k$ is an integer. Since the three variables of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ take values that are respectively located within the three following distinct intervals $[0, 2]$ , $[3, 5]$ and $[9, 11]$ , the $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕$ constraint holds.

All solutions

Figure 5.17.1 gives all solutions to the following non ground instance of the $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕 0$ constraint: $V_{1} \in [0, 7]$ , $V_{2} \in [1, 2]$ , $V_{3} \in [2, 3]$ , $V_{4} \in [0, 9]$ , $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕 0$ $(〈 V_{1}, V_{2}, V_{3}, V_{4} 〉, 3)$ .

Figure 5.17.1. All solutions corresponding to the non ground example of the $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕 0$ constraint of the All solutions slot

Typical

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | > 1

𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻 > 1

𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻 <

𝚛𝚊𝚗𝚐𝚎

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛)

Symmetries

Items of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ are permutable.
A value of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛$ that belongs to the $k$ -th interval, of size $𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻$ , can be renamed to any unused value of the same interval.
Two distinct values of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛$ that belong to two distinct intervals, of size $𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻$ , can be swapped.

Arg. properties

Contractible wrt. $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ .

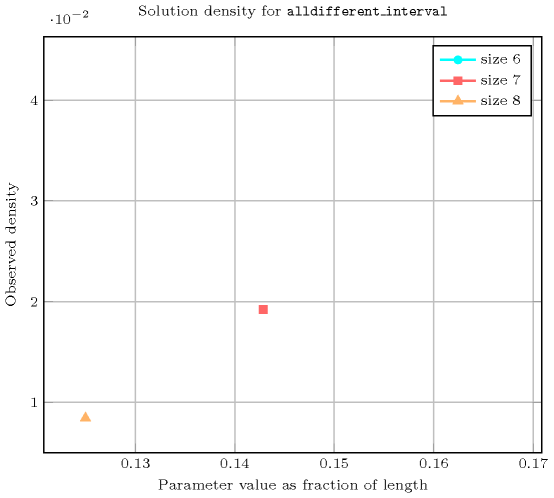
Counting

Length ( $n$ )	2	3	4	5	6	7	8
Solutions	10	24	120	720	5040	40320	362880

Number of solutions for $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕$ : domains $0 . . n$

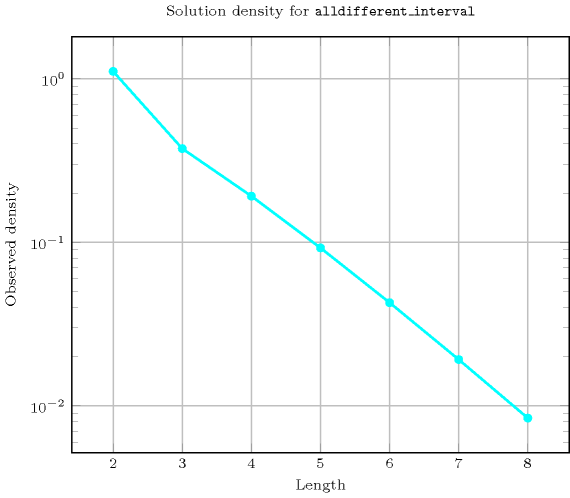
ctrs/alldifferent_interval-2-tikz

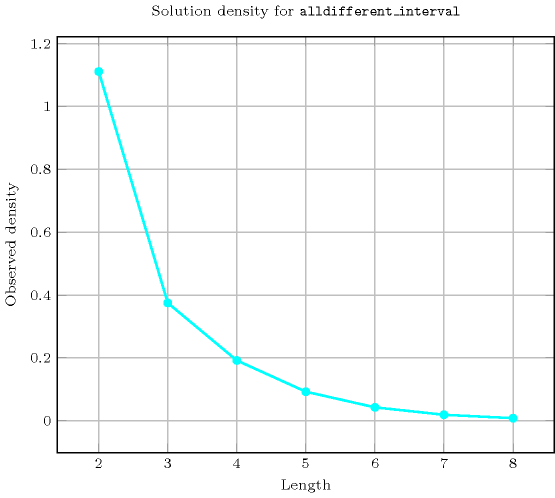
ctrs/alldifferent_interval-3-tikz

Length (

n

)

Total

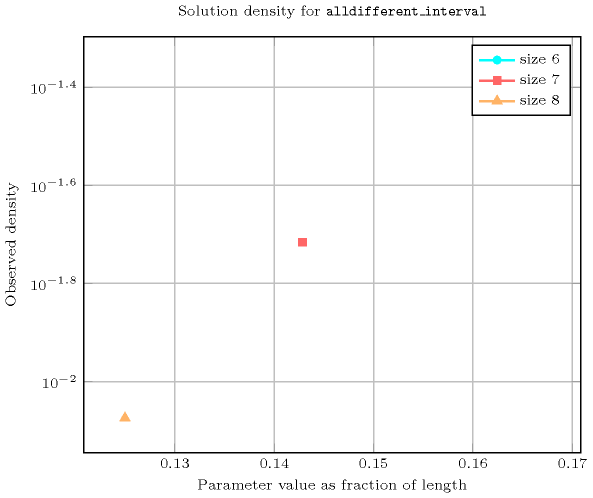
120

720

5040

40320

362880

Parameter

value

120

720

5040

40320

362880

Solution count for $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕$ : domains $0 . . n$

ctrs/alldifferent_interval-4-tikz

ctrs/alldifferent_interval-5-tikz

See also

implied by: $𝚊𝚕𝚕_𝚖𝚒𝚗_𝚍𝚒𝚜𝚝$ .

specialisation: $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝$ ( $𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎 / 𝚌𝚘𝚗𝚜𝚝𝚊𝚗𝚝$ replaced by $𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎$ ).

Keywords

characteristic of a constraint: all different, sort based reformulation, automaton, automaton with array of counters.

constraint type: value constraint.

filtering: arc-consistency.

final graph structure: one_succ.

modelling: interval.

Arc input(s)

$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$

Arc generator

𝐶𝐿𝐼𝑄𝑈𝐸

\mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 1, 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 2)

Arc arity

Arc constraint(s)

\begin{matrix} 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 1 . 𝚟𝚊𝚛 / 𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻 = \\ 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 2 . 𝚟𝚊𝚛 / 𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻 \end{matrix}

Graph property(ies)

𝐌𝐀𝐗_𝐍𝐒𝐂𝐂

\leq 1

Graph class

𝙾𝙽𝙴_𝚂𝚄𝙲𝙲

Graph model

Similar to the $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝$ constraint, but we replace the binary equality constraint of the $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝$ constraint by the fact that two variables are respectively assigned to two values that belong to the same interval. We generate a clique with a belong to the same interval constraint between each pair of vertices (including a vertex and itself) and state that the size of the largest strongly connected component should not exceed 1.

Parts (A) and (B) of Figure 5.17.2 respectively show the initial and final graph associated with the Example slot. Since we use the $𝐌𝐀𝐗_𝐍𝐒𝐂𝐂$ graph property we show one of the largest strongly connected component of the final graph.

Figure 5.17.2. Initial and final graph of the $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕$ constraint


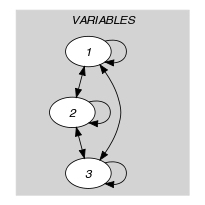
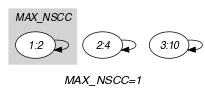
(a)	(b)

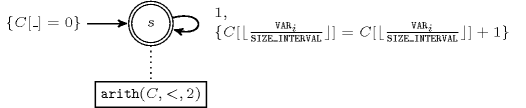
Automaton: Figure 5.17.3 depicts the automaton associated with the $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕$ constraint. To each item of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ corresponds a signature variable $𝚂_{i}$ that is equal to 1. For each interval $[𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻 \cdot k, 𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻 \cdot k + 𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻 - 1]$ of values the automaton counts the number of occurrences of its values and finally imposes that the values of an interval are taken at most once.

Figure 5.17.3. Automaton of the $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕$ constraint

Global Constraint Catalog

5. Global Constraint Catalogue

5.17. alldifferent_interval

Figure 5.17.1. All solutions corresponding to the non ground example of the $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕 0$ constraint of the All solutions slot

Figure 5.17.2. Initial and final graph of the $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕$ constraint

Figure 5.17.3. Automaton of the $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕$ constraint

Global Constraint Catalog

5. Global Constraint Catalogue

5.17. alldifferent_interval

Figure 5.17.1. All solutions corresponding to the non ground example of the 𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕0 constraint of the All solutions slot

Figure 5.17.2. Initial and final graph of the 𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕 constraint

Figure 5.17.3. Automaton of the 𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕 constraint

Figure 5.17.1. All solutions corresponding to the non ground example of the $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕 0$ constraint of the All solutions slot

Figure 5.17.2. Initial and final graph of the $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕$ constraint

Figure 5.17.3. Automaton of the $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕$ constraint