Global Constraint Catalog: Csoft_same_partition

5.364. soft_same_partition_var

DESCRIPTION

LINKS

GRAPH

Origin

Derived from $𝚜𝚊𝚖𝚎_𝚙𝚊𝚛𝚝𝚒𝚝𝚒𝚘𝚗$

Constraint

$𝚜𝚘𝚏𝚝_𝚜𝚊𝚖𝚎_𝚙𝚊𝚛𝚝𝚒𝚝𝚒𝚘𝚗_𝚟𝚊𝚛 (𝙲, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2, 𝙿𝙰𝚁𝚃𝙸𝚃𝙸𝙾𝙽𝚂)$

Synonym

$𝚜𝚘𝚏𝚝_𝚜𝚊𝚖𝚎_𝚙𝚊𝚛𝚝𝚒𝚝𝚒𝚘𝚗$ .

Type

𝚅𝙰𝙻𝚄𝙴𝚂

𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚕 - 𝚒𝚗𝚝)

Arguments

$𝙲$	$𝚍𝚟𝚊𝚛$
$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛)$
$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛)$
$𝙿𝙰𝚁𝚃𝙸𝚃𝙸𝙾𝙽𝚂$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚙 - 𝚅𝙰𝙻𝚄𝙴𝚂)$

Restrictions

𝙲 \geq 0

𝙲 \leq | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 |

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 | = | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 |

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1, 𝚟𝚊𝚛)

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2, 𝚟𝚊𝚛)

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝙿𝙰𝚁𝚃𝙸𝚃𝙸𝙾𝙽𝚂, 𝚙)

| 𝙿𝙰𝚁𝚃𝙸𝚃𝙸𝙾𝙽𝚂 | \geq 2

| 𝚅𝙰𝙻𝚄𝙴𝚂 | \geq 1

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝙻𝚄𝙴𝚂, 𝚟𝚊𝚕)

𝚍𝚒𝚜𝚝𝚒𝚗𝚌𝚝

(𝚅𝙰𝙻𝚄𝙴𝚂, 𝚟𝚊𝚕)

Purpose

For each integer $i$ in $[1, | 𝙿𝙰𝚁𝚃𝙸𝚃𝙸𝙾𝙽𝚂 |]$ , let $𝑁 1_{i}$ (respectively $𝑁 2_{i}$ ) denote the number of variables of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ (respectively $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ ) that take their value in the $i^{t h}$ partition of the collection $𝙿𝙰𝚁𝚃𝙸𝚃𝙸𝙾𝙽𝚂$ . $𝙲$ is the minimum number of values to change in the $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ and $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ collections so that for all $i$ in $[1, | 𝙿𝙰𝚁𝚃𝙸𝚃𝙸𝙾𝙽𝚂 |]$ we have $𝑁 1_{i} = 𝑁 2_{i}$ .

Example

(\begin{matrix} 4, 〈9, 9, 9, 9, 9, 1〉, \\ 〈9, 1, 1, 1, 1, 8〉, \\ 〈𝚙 - 〈1, 2〉, 𝚙 - 〈9〉, 𝚙 - 〈7, 8〉〉 \end{matrix})

In the example, the values of the collections $〈 9, 9, 9, 9, 9, 1 〉$ and $〈 9, 1, 1, 1, 1, 8 〉$ are respectively associated with the partitions $𝚙 - 〈 9 〉$ , $𝚙 - 〈 9 〉$ , $𝚙 - 〈 9 〉$ , $𝚙 - 〈 9 〉$ , $𝚙 - 〈 9 〉$ , $𝚙 - 〈 1, 2 〉$ and $𝚙 - 〈 9 〉$ , $𝚙 - 〈 1, 2 〉$ , $𝚙 - 〈 1, 2 〉$ , $𝚙 - 〈 1, 2 〉$ , $𝚙 - 〈 1, 2 〉$ , $𝚙 - 〈 7, 8 〉$ . Since there is a correspondence between two pairs of partitions we must unset at least $6 - 2$ items (6 is the number of items of the $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ and $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ collections). Consequently, the $𝚜𝚘𝚏𝚝_𝚜𝚊𝚖𝚎_𝚙𝚊𝚛𝚝𝚒𝚝𝚒𝚘𝚗_𝚟𝚊𝚛$ constraint holds since its first argument $𝙲$ is set to $6 - 2$ .

Typical

𝙲 > 0

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 | > 1

𝚛𝚊𝚗𝚐𝚎

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 . 𝚟𝚊𝚛) > 1

𝚛𝚊𝚗𝚐𝚎

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 . 𝚟𝚊𝚛) > 1

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 | > | 𝙿𝙰𝚁𝚃𝙸𝚃𝙸𝙾𝙽𝚂 |

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 | > | 𝙿𝙰𝚁𝚃𝙸𝚃𝙸𝙾𝙽𝚂 |

Symmetries

Arguments are permutable w.r.t. permutation $(𝙲)$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2)$ $(𝙿𝙰𝚁𝚃𝙸𝚃𝙸𝙾𝙽𝚂)$ .
Items of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ are permutable.
Items of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ are permutable.
Items of $𝙿𝙰𝚁𝚃𝙸𝚃𝙸𝙾𝙽𝚂$ are permutable.
Items of $𝙿𝙰𝚁𝚃𝙸𝚃𝙸𝙾𝙽𝚂 . 𝚙$ are permutable.
An occurrence of a value of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 . 𝚟𝚊𝚛$ can be replaced by any other value that also belongs to the same partition of $𝙿𝙰𝚁𝚃𝙸𝚃𝙸𝙾𝙽𝚂$ .
An occurrence of a value of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 . 𝚟𝚊𝚛$ can be replaced by any other value that also belongs to the same partition of $𝙿𝙰𝚁𝚃𝙸𝚃𝙸𝙾𝙽𝚂$ .

Usage

A soft $𝚜𝚊𝚖𝚎_𝚙𝚊𝚛𝚝𝚒𝚝𝚒𝚘𝚗$ constraint.

Algorithm

See algorithm of the $𝚜𝚘𝚏𝚝_𝚜𝚊𝚖𝚎_𝚟𝚊𝚛$ constraint.

See also

hard version: $𝚜𝚊𝚖𝚎_𝚙𝚊𝚛𝚝𝚒𝚝𝚒𝚘𝚗$ .

implies: $𝚜𝚘𝚏𝚝_𝚞𝚜𝚎𝚍_𝚋𝚢_𝚙𝚊𝚛𝚝𝚒𝚝𝚒𝚘𝚗_𝚟𝚊𝚛$ .

Keywords

characteristic of a constraint: partition.

constraint arguments: constraint between two collections of variables.

constraint type: soft constraint, relaxation, variable-based violation measure.

Arc input(s)

$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$

Arc generator

𝑃𝑅𝑂𝐷𝑈𝐶𝑇

\mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 1, 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 2)

Arc arity

Arc constraint(s)

𝚒𝚗_𝚜𝚊𝚖𝚎_𝚙𝚊𝚛𝚝𝚒𝚝𝚒𝚘𝚗

(𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 1 . 𝚟𝚊𝚛, 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 2 . 𝚟𝚊𝚛, 𝙿𝙰𝚁𝚃𝙸𝚃𝙸𝙾𝙽𝚂)

Graph property(ies)

𝐍𝐒𝐈𝐍𝐊_𝐍𝐒𝐎𝐔𝐑𝐂𝐄

= | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 | - 𝙲

Graph model

Parts (A) and (B) of Figure 5.364.1 respectively show the initial and final graph associated with the Example slot. Since we use the $𝐍𝐒𝐈𝐍𝐊_𝐍𝐒𝐎𝐔𝐑𝐂𝐄$ graph property, the source and sink vertices of the final graph are stressed with a double circle. The $𝚜𝚘𝚏𝚝_𝚜𝚊𝚖𝚎_𝚙𝚊𝚛𝚝𝚒𝚝𝚒𝚘𝚗_𝚟𝚊𝚛$ constraint holds since the cost 4 corresponds to the difference between the number of variables of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ and the sum over the different connected components of the minimum number of sources and sinks.

Figure 5.364.1. Initial and final graph of the $𝚜𝚘𝚏𝚝_𝚜𝚊𝚖𝚎_𝚙𝚊𝚛𝚝𝚒𝚝𝚒𝚘𝚗_𝚟𝚊𝚛$ constraint

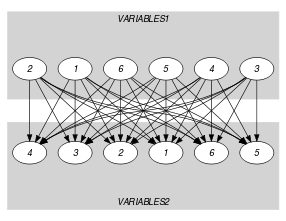
(a)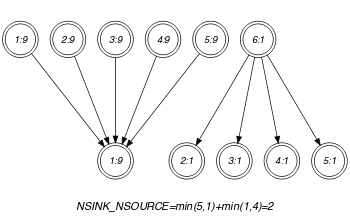

(b)

Global Constraint Catalog

5. Global Constraint Catalogue

5.364. soft_same_partition_var

Figure 5.364.1. Initial and final graph of the 𝚜𝚘𝚏𝚝_𝚜𝚊𝚖𝚎_𝚙𝚊𝚛𝚝𝚒𝚝𝚒𝚘𝚗_𝚟𝚊𝚛 constraint

Figure 5.364.1. Initial and final graph of the $𝚜𝚘𝚏𝚝_𝚜𝚊𝚖𝚎_𝚙𝚊𝚛𝚝𝚒𝚝𝚒𝚘𝚗_𝚟𝚊𝚛$ constraint