5.178. in_interval
| DESCRIPTION | LINKS | GRAPH | AUTOMATON |
- Origin
Domain definition.
- Constraint
- Synonyms
, .
- Arguments
- Restriction
- Purpose
Enforce the domain variable to take a value within the interval .
- Example
-
The constraint holds since its first argument is greater than or equal to its second argument and less than or equal to its third argument .
- Typical
- Symmetries
- Remark
Entailment occurs immediately after posting this constraint.
The constraint is referenced under the name in Gecode.
- Systems
- See also
common keyword: , (domain definition).
generalisation: (reified version), (single interval replaced by a set of intervals), (interval replaced by set variable).
- Keywords
characteristic of a constraint: automaton, automaton without counters, reified automaton constraint, derived collection.
constraint arguments: unary constraint.
constraint network structure: Berge-acyclic constraint network.
- Derived Collections
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
-
- Graph property(ies)
-
- Graph model
Parts (A) and (B) of Figure 5.178.1 respectively show the initial and final graph associated with the Example slot. Since we use the graph property, the unique arc of the final graph is stressed in bold.
Figure 5.178.1. Initial and final graph of the constraint
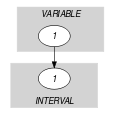
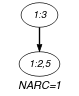
(a) (b)
- Automaton
Figure 5.178.2 depicts the automaton associated with the constraint. We have a single 0-1 signature variable as well as the following signature constraint: .
Figure 5.178.2. Automaton of the constraint
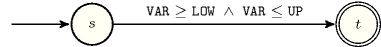
Figure 5.178.3. Hypergraph of the reformulation corresponding to the automaton of the constraint