5.31. arith
| DESCRIPTION | LINKS | GRAPH | AUTOMATON |
- Origin
Used in the definition of several automata
- Constraint
- Synonym
.
- Arguments
- Restrictions
- Purpose
Enforce for all variables of the collection to have .
- Example
-
The constraint holds since all values of the collection are strictly less than 9.
- Typical
- Symmetries
Items of are permutable.
An occurrence of a value of can be replaced by any value of .
- Arg. properties
Contractible wrt. .
- Systems
eq in Choco, neq in Choco, geq in Choco, gt in Choco, leq in Choco, lt in Choco, rel in Gecode, #< in SICStus, #=< in SICStus, #> in SICStus, #>= in SICStus, #= in SICStus, #\= in SICStus.
- Used in
- See also
common keyword: , (value constraint).
generalisation: ( replaced by ).
- Keywords
characteristic of a constraint: automaton, automaton without counters, reified automaton constraint.
constraint network structure: Berge-acyclic constraint network.
- Cond. implications
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
- Graph property(ies)
-
- Graph model
Parts (A) and (B) of Figure 5.31.1 respectively show the initial and final graph associated with the Example slot. Since we use the graph property, the loops of the final graph are stressed in bold.
Figure 5.31.1. Initial and final graph of the constraint


(a) (b)
- Automaton
Figure 5.31.2 depicts the automaton associated with the constraint. To each variable of the collection corresponds a 0-1 signature variable . The following signature constraint links and : . The automaton enforces for each variable the condition .
Figure 5.31.2. Automaton of the constraint
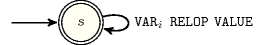
Figure 5.31.3. Hypergraph of the reformulation corresponding to the automaton of the constraint