Global Constraint Catalog: Call_equal

5.8. all_equal_valley

DESCRIPTION

LINKS

AUTOMATON

Origin

Derived from $𝚟𝚊𝚕𝚕𝚎𝚢$ and $𝚊𝚕𝚕_𝚎𝚚𝚞𝚊𝚕$ .

Constraint

$𝚊𝚕𝚕_𝚎𝚚𝚞𝚊𝚕_𝚟𝚊𝚕𝚕𝚎𝚢 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

Argument

𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂

𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛)

Restrictions

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | > 0

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚟𝚊𝚛)

Purpose

A variable $V_{k}$ $(1 < k < m)$ of the sequence of variables $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 = V_{1}, \dots, V_{m}$ is a valley if and only if there exists an $i$ $(1 < i \leq k)$ such that $V_{i - 1} > V_{i}$ and $V_{i} = V_{i + 1} = \dots = V_{k}$ and $V_{k} < V_{k + 1}$ .

Enforce all the valleys of the sequence $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ to be assigned the same value, i.e. to be located at the same altitude.

Example

(〈1, 5, 5, 4, 2, 2, 6, 2, 7〉)

The $𝚊𝚕𝚕_𝚎𝚚𝚞𝚊𝚕_𝚟𝚊𝚕𝚕𝚎𝚢$ constraint holds since the two valleys, in bold, of the sequence $155422627$ are located at the same altitude 2. Figure 5.8.1 depicts the solution associated with the example.

Figure 5.8.1. Illustration of the Example slot: a sequence of nine variables $V_{1}$ , $V_{2}$ , $V_{3}$ , $V_{4}$ , $V_{5}$ , $V_{6}$ , $V_{7}$ , $V_{8}$ , $V_{9}$ respectively fixed to values 1, 5, 5, 4, 2, 2, 6, 2, 7 and its corresponding two valleys, in red, both located at altitude 2

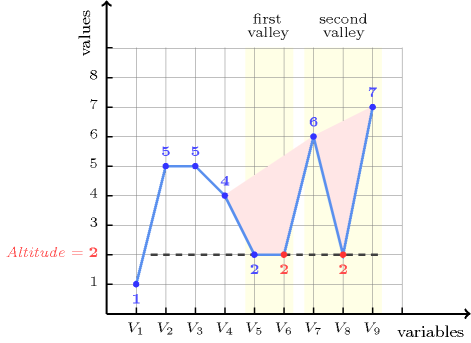
Note that the $𝚊𝚕𝚕_𝚎𝚚𝚞𝚊𝚕_𝚟𝚊𝚕𝚕𝚎𝚢$ constraint does not enforce that the minimum value of the sequence $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ corresponds to the altitude of its valleys since, as shown by the example, the sequence can starts with an increasing subsequence that start below the altitude of its valleys. It also does not enforce that the sequence $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ contains at least one valley.

Typical

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | \geq 5

𝚛𝚊𝚗𝚐𝚎

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛) > 1

𝚟𝚊𝚕𝚕𝚎𝚢

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛) \geq 2

Symmetries

Items of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ can be reversed.
One and the same constant can be added to the $𝚟𝚊𝚛$ attribute of all items of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ .

Arg. properties

Prefix-contractible wrt. $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ .
Suffix-contractible wrt. $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ .

Counting

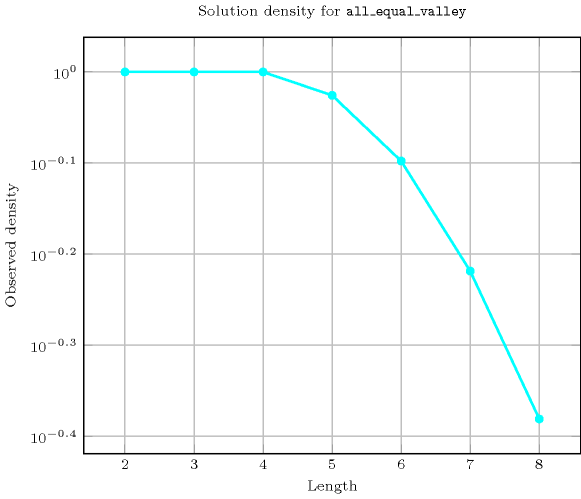
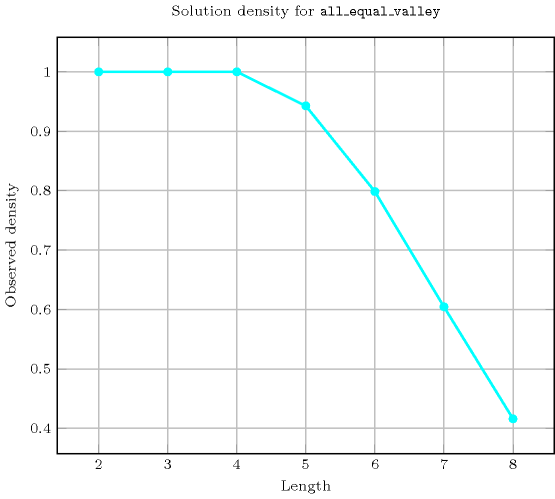
Length ( $n$ )	2	3	4	5	6	7	8
Solutions	9	64	625	7330	93947	1267790	17908059

Number of solutions for $𝚊𝚕𝚕_𝚎𝚚𝚞𝚊𝚕_𝚟𝚊𝚕𝚕𝚎𝚢$ : domains $0 . . n$

ctrs/all_equal_valley-2-tikz

ctrs/all_equal_valley-3-tikz

implies: $𝚍𝚎𝚌𝚛𝚎𝚊𝚜𝚒𝚗𝚐_𝚟𝚊𝚕𝚕𝚎𝚢$ , $𝚒𝚗𝚌𝚛𝚎𝚊𝚜𝚒𝚗𝚐_𝚟𝚊𝚕𝚕𝚎𝚢$ .

Keywords

characteristic of a constraint: automaton, automaton with counters, automaton with same input symbol.

combinatorial object: sequence.

constraint network structure: sliding cyclic(1) constraint network(2).

Cond. implications

$•$ $𝚊𝚕𝚕_𝚎𝚚𝚞𝚊𝚕_𝚟𝚊𝚕𝚕𝚎𝚢 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

with $𝚟𝚊𝚕𝚕𝚎𝚢$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛) > 1$

implies $𝚜𝚘𝚖𝚎_𝚎𝚚𝚞𝚊𝚕$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ .

$•$ $𝚊𝚕𝚕_𝚎𝚚𝚞𝚊𝚕_𝚟𝚊𝚕𝚕𝚎𝚢 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

with $𝚟𝚊𝚕𝚕𝚎𝚢$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛) > 0$

implies $𝚗𝚘𝚝_𝚊𝚕𝚕_𝚎𝚚𝚞𝚊𝚕$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ .

Automaton: Figure 5.8.2 depicts the automaton associated with the $𝚊𝚕𝚕_𝚎𝚚𝚞𝚊𝚕_𝚟𝚊𝚕𝚕𝚎𝚢$ constraint. To each pair of consecutive variables $({𝚅𝙰𝚁}_{i}, {𝚅𝙰𝚁}_{i + 1})$ of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ corresponds a signature variable $S_{i}$ . The following signature constraint links ${𝚅𝙰𝚁}_{i}$ , ${𝚅𝙰𝚁}_{i + 1}$ and $S_{i}$ : $({𝚅𝙰𝚁}_{i} < {𝚅𝙰𝚁}_{i + 1} \Leftrightarrow S_{i} = 0) \land ({𝚅𝙰𝚁}_{i} = {𝚅𝙰𝚁}_{i + 1} \Leftrightarrow S_{i} = 1) \land ({𝚅𝙰𝚁}_{i} > {𝚅𝙰𝚁}_{i + 1} \Leftrightarrow S_{i} = 2)$ .

Figure 5.8.2. Automaton for the $𝚊𝚕𝚕_𝚎𝚚𝚞𝚊𝚕_𝚟𝚊𝚕𝚕𝚎𝚢$ constraint (note the conditional transition from state $k$ to state $j$ testing that the counter $𝐴𝑙𝑡𝑖𝑡𝑢𝑑𝑒$ is equal to ${𝚅𝙰𝚁}_{i}$ for enforcing that all valleys are located at the same altitude)

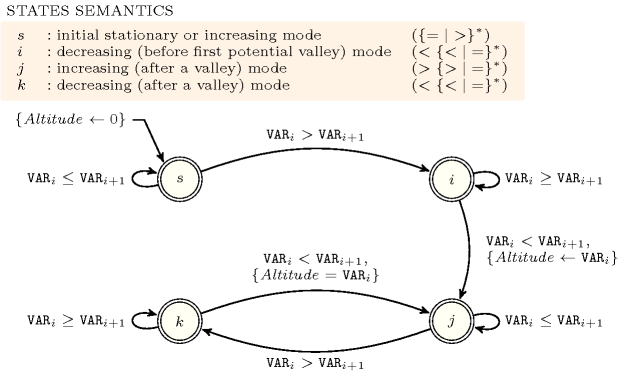
Figure 5.8.3. Hypergraph of the reformulation corresponding to the automaton of the $𝚊𝚕𝚕_𝚎𝚚𝚞𝚊𝚕_𝚟𝚊𝚕𝚕𝚎𝚢$ constraint where $A_{i}$ stands for the value of the counter $𝐴𝑙𝑡𝑖𝑡𝑢𝑑𝑒$ (since all states of the automaton are accepting there is no restriction on the last variable $Q_{n - 1}$ )

Global Constraint Catalog

5. Global Constraint Catalogue

5.8. all_equal_valley

Figure 5.8.1. Illustration of the Example slot: a sequence of nine variables V 1 , V 2 , V 3 , V 4 , V 5 , V 6 , V 7 , V 8 , V 9 respectively fixed to values 1, 5, 5, 4, 2, 2, 6, 2, 7 and its corresponding two valleys, in red, both located at altitude 2

Figure 5.8.1. Illustration of the Example slot: a sequence of nine variables $V_{1}$ , $V_{2}$ , $V_{3}$ , $V_{4}$ , $V_{5}$ , $V_{6}$ , $V_{7}$ , $V_{8}$ , $V_{9}$ respectively fixed to values 1, 5, 5, 4, 2, 2, 6, 2, 7 and its corresponding two valleys, in red, both located at altitude 2