5.279. no_valley
| DESCRIPTION | LINKS | AUTOMATON |
- Origin
- Constraint
- Argument
- Restrictions
- Purpose
A variable of the sequence of variables is a valley if and only if there exists an such that and and . The total number of valleys of the sequence of variables is equal to 0.
- Example
-
The constraint holds since the sequence does not contain any valley.
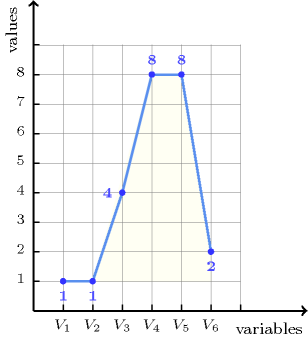
Figure 5.279.1. Illustration of the Example slot: a sequence of five variables , , , , , respectively fixed to values 1, 1, 4, 8, 8, 2 without any valley
- Typical
- Symmetries
- Arg. properties
Contractible wrt. .
- Counting
-
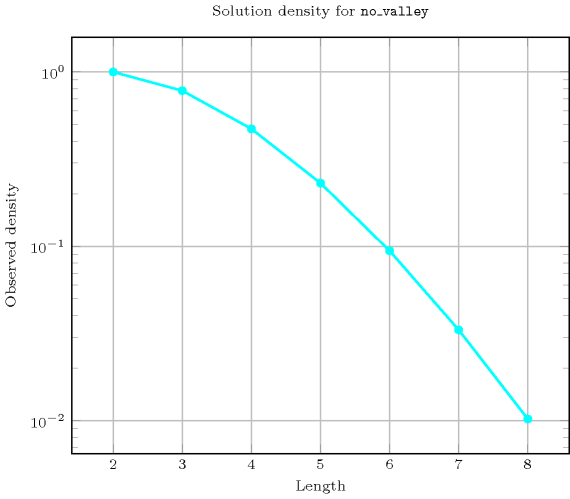
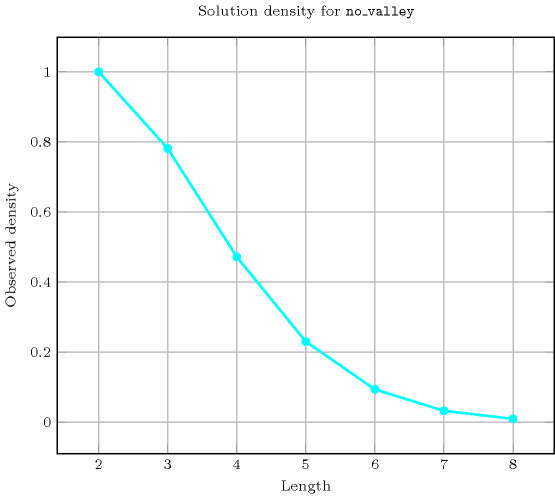
Length () 2 3 4 5 6 7 8 Solutions 9 50 295 1792 11088 69498 439791 Number of solutions for : domains
- See also
-
generalisation: (introduce a counting the number of valleys).
implied by: , , .
implies: .
related: .
- Keywords
characteristic of a constraint: automaton, automaton without counters, automaton with same input symbol, reified automaton constraint.
combinatorial object: sequence.
constraint network structure: sliding cyclic(1) constraint network(1).
- Automaton
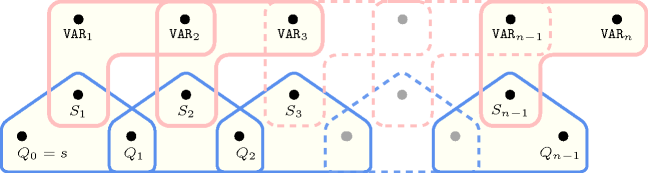
Figure 5.279.2 depicts the automaton associated with the constraint. To each pair of consecutive variables of the collection corresponds a signature variable . The following signature constraint links , and : .
Figure 5.279.2. Automaton of the constraint
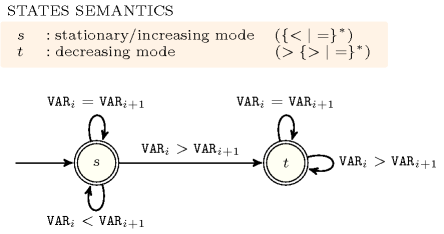
Figure 5.279.3. Hypergraph of the reformulation corresponding to the automaton of the constraint (since all states of the automaton are accepting there is no restriction on the last variable )