Global Constraint Catalog: Cnvalues_except

5.289. nvalues_except_0

DESCRIPTION

LINKS

GRAPH

Origin

Derived from $𝚗𝚟𝚊𝚕𝚞𝚎𝚜$ .

Constraint

$𝚗𝚟𝚊𝚕𝚞𝚎𝚜_𝚎𝚡𝚌𝚎𝚙𝚝_0 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚁𝙴𝙻𝙾𝙿, 𝙻𝙸𝙼𝙸𝚃)$

Arguments

$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛)$
$𝚁𝙴𝙻𝙾𝙿$	$𝚊𝚝𝚘𝚖$
$𝙻𝙸𝙼𝙸𝚃$	$𝚍𝚟𝚊𝚛$

Restrictions

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚟𝚊𝚛)

𝚁𝙴𝙻𝙾𝙿 \in [=, \neq, <, \geq, >, \leq]

Purpose

Let $N$ be the number of distinct values, different from 0, assigned to the variables of the $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ collection. Enforce condition $N 𝚁𝙴𝙻𝙾𝙿 𝙻𝙸𝙼𝙸𝚃$ to hold.

Example

(〈4, 5, 5, 4, 0, 1〉, =, 3)

The $𝚗𝚟𝚊𝚕𝚞𝚎𝚜_𝚎𝚡𝚌𝚎𝚙𝚝_0$ constraint holds since the number of distinct values, different from 0, occurring within the collection $〈 4, 5, 5, 4, 0, 1 〉$ is equal (i.e., $𝚁𝙴𝙻𝙾𝙿$ is set to $=$ ) to its third argument $𝙻𝙸𝙼𝙸𝚃 = 3$ .

Typical

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | > 1

𝙻𝙸𝙼𝙸𝚃 > 1

𝙻𝙸𝙼𝙸𝚃 < | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 |

𝚊𝚝𝚕𝚎𝚊𝚜𝚝

(1, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 0)

𝚁𝙴𝙻𝙾𝙿 \in [=, <, \geq, >, \leq]

Symmetries

Items of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ are permutable.
All occurrences of two distinct values of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛$ that are both different from 0 can be swapped; all occurrences of a value of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛$ that is different from 0 can be renamed to any unused value that is also different from 0.

Arg. properties

Contractible wrt. $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ when $𝚁𝙴𝙻𝙾𝙿 \in [<, \leq]$ .
Extensible wrt. $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ when $𝚁𝙴𝙻𝙾𝙿 \in [\geq, >]$ .

Reformulation

The $𝚗𝚟𝚊𝚕𝚞𝚎𝚜_𝚎𝚡𝚌𝚎𝚙𝚝_0$ $(〈 V_{1}, V_{2}, \dots, V_{| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 |} 〉, 𝚁𝙴𝙻𝙾𝙿, 𝙻𝙸𝙼𝙸𝚃)$ constraint can be expressed in term of the conjunction $𝚗𝚟𝚊𝚕𝚞𝚎$ $(𝑁𝑉 1, 〈 0, V_{1}, V_{2}, \dots, V_{| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 |} 〉)$ $\land$ $𝑁𝑉 1 - 1 𝚁𝙴𝙻𝙾𝙿 𝙻𝙸𝙼𝙸𝚃$ .

Used in

$𝚌𝚢𝚌𝚕𝚎_𝚘𝚛_𝚊𝚌𝚌𝚎𝚜𝚜𝚒𝚋𝚒𝚕𝚒𝚝𝚢$ .

$𝚗𝚟𝚊𝚕𝚞𝚎$ , $𝚗𝚟𝚊𝚕𝚞𝚎𝚜$ (counting constraint,number of distinct values).

Keywords

characteristic of a constraint: joker value.

constraint type: counting constraint, value partitioning constraint.

final graph structure: strongly connected component.

modelling: number of distinct values.

Arc input(s)

$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$

Arc generator

𝐶𝐿𝐼𝑄𝑈𝐸

\mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 1, 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 2)

Arc arity

Arc constraint(s)

• 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 1 . 𝚟𝚊𝚛 \neq 0

• 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 1 . 𝚟𝚊𝚛 = 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 2 . 𝚟𝚊𝚛

Graph property(ies)

𝐍𝐒𝐂𝐂

𝚁𝙴𝙻𝙾𝙿 𝙻𝙸𝙼𝙸𝚃

Graph model

Parts (A) and (B) of Figure 5.289.1 respectively show the initial and final graph associated with the Example slot. Since we use the $𝐍𝐒𝐂𝐂$ graph property we show the different strongly connected components of the final graph. Each strongly connected component corresponds to a value distinct from 0 that is assigned to some variables of the $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ collection. Beside value 0, the 3 following values 1, 4 and 5 are assigned to the variables of the $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ collection.

Figure 5.289.1. Initial and final graph of the $𝚗𝚟𝚊𝚕𝚞𝚎𝚜_𝚎𝚡𝚌𝚎𝚙𝚝_0$ constraint


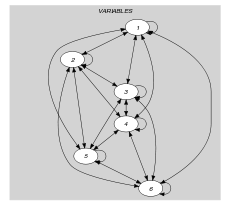
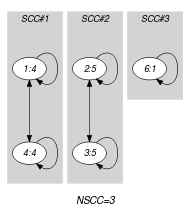
(a)	(b)

Global Constraint Catalog

5. Global Constraint Catalogue

5.289. nvalues_except_0

Figure 5.289.1. Initial and final graph of the 𝚗𝚟𝚊𝚕𝚞𝚎𝚜_𝚎𝚡𝚌𝚎𝚙𝚝_0 constraint

Figure 5.289.1. Initial and final graph of the $𝚗𝚟𝚊𝚕𝚞𝚎𝚜_𝚎𝚡𝚌𝚎𝚙𝚝_0$ constraint