Global Constraint Catalog: Csliding_card

5.349. sliding_card_skip0

DESCRIPTION

LINKS

GRAPH

AUTOMATON

Origin

N. Beldiceanu

Constraint

$𝚜𝚕𝚒𝚍𝚒𝚗𝚐_𝚌𝚊𝚛𝚍_𝚜𝚔𝚒𝚙 0 (𝙰𝚃𝙻𝙴𝙰𝚂𝚃, 𝙰𝚃𝙼𝙾𝚂𝚃, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚅𝙰𝙻𝚄𝙴𝚂)$

Arguments

$𝙰𝚃𝙻𝙴𝙰𝚂𝚃$	$𝚒𝚗𝚝$
$𝙰𝚃𝙼𝙾𝚂𝚃$	$𝚒𝚗𝚝$
$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛)$
$𝚅𝙰𝙻𝚄𝙴𝚂$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚕 - 𝚒𝚗𝚝)$

Restrictions

𝙰𝚃𝙻𝙴𝙰𝚂𝚃 \geq 0

𝙰𝚃𝙻𝙴𝙰𝚂𝚃 \leq | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 |

𝙰𝚃𝙼𝙾𝚂𝚃 \geq 0

𝙰𝚃𝙼𝙾𝚂𝚃 \leq | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 |

𝙰𝚃𝙼𝙾𝚂𝚃 \geq 𝙰𝚃𝙻𝙴𝙰𝚂𝚃

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚟𝚊𝚛)

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝙻𝚄𝙴𝚂, 𝚟𝚊𝚕)

𝚍𝚒𝚜𝚝𝚒𝚗𝚌𝚝

(𝚅𝙰𝙻𝚄𝙴𝚂, 𝚟𝚊𝚕)

𝚅𝙰𝙻𝚄𝙴𝚂 . 𝚟𝚊𝚕 \neq 0

Purpose

Let $n$ be the total number of variables of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ . A maximum non-zero set of consecutive variables $X_{i} . . X_{j} (1 \leq i \leq j \leq n)$ is defined in the following way:

All variables $X_{i}, \dots, X_{j}$ take a non-zero value,
$i = 1$ or $X_{i - 1}$ is equal to 0,
$j = n$ or $X_{j + 1}$ is equal to 0.

Enforces that each maximum non-zero set of consecutive variables of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ contains at least $𝙰𝚃𝙻𝙴𝙰𝚂𝚃$ and at most $𝙰𝚃𝙼𝙾𝚂𝚃$ values from the collection of values $𝚅𝙰𝙻𝚄𝙴𝚂$ .

Example

(2, 3, 〈0, 7, 2, 9, 0, 0, 9, 4, 9〉, 〈7, 9〉)

The $𝚜𝚕𝚒𝚍𝚒𝚗𝚐_𝚌𝚊𝚛𝚍_𝚜𝚔𝚒𝚙 0$ constraint holds since the two maximum non-zero set of consecutive values $729$ and $949$ of its third argument $〈 0, 7, 2, 9, 0, 0, 9, 4, 9 〉$ take both 2 ( $2 \in [𝙰𝚃𝙻𝙴𝙰𝚂𝚃, 𝙰𝚃𝙼𝙾𝚂𝚃] = [2, 3]$ ) values within the set of values $〈 7, 9 〉$ .

Typical

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | > 1

| 𝚅𝙰𝙻𝚄𝙴𝚂 | > 0

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | > | 𝚅𝙰𝙻𝚄𝙴𝚂 |

𝚊𝚝𝚕𝚎𝚊𝚜𝚝

(1, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 0)

𝙰𝚃𝙻𝙴𝙰𝚂𝚃 > 0 \lor 𝙰𝚃𝙼𝙾𝚂𝚃 < | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 |

Symmetries

$𝙰𝚃𝙻𝙴𝙰𝚂𝚃$ can be decreased to any value $\geq 0$ .
$𝙰𝚃𝙼𝙾𝚂𝚃$ can be increased to any value $\leq | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 |$ .
Items of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ can be reversed.
An occurrence of a value different from 0 of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛$ that belongs to $𝚅𝙰𝙻𝚄𝙴𝚂 . 𝚟𝚊𝚕$ (resp. does not belong to $𝚅𝙰𝙻𝚄𝙴𝚂 . 𝚟𝚊𝚕$ ) can be replaced by any other value different from 0 in $𝚅𝙰𝙻𝚄𝙴𝚂 . 𝚟𝚊𝚕$ (resp. not in $𝚅𝙰𝙻𝚄𝙴𝚂 . 𝚟𝚊𝚕$ ).

Usage

This constraint is useful in timetabling problems where the variables are interpreted as the type of job that a person does on consecutive days. Value 0 represents a rest day and one imposes a cardinality constraint on periods that are located between rest periods.

Remark

One cannot initially state a $𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢$ constraint since the rest days are not yet allocated. One can also not use an $𝚊𝚖𝚘𝚗𝚐_𝚜𝚎𝚚$ constraint since it does not hold for the sequences of consecutive variables that contains at least one rest day.

See also

related: $𝚊𝚖𝚘𝚗𝚐$ (counting constraint on the full sequence), $𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢$ (counting constraint for different values on the full sequence).

specialisation: $𝚊𝚖𝚘𝚗𝚐_𝚕𝚘𝚠_𝚞𝚙$ (maximal sequences replaced by the full sequence).

Keywords

characteristic of a constraint: automaton, automaton with counters.

combinatorial object: sequence.

constraint network structure: alpha-acyclic constraint network(2).

constraint type: timetabling constraint, sliding sequence constraint.

Arc input(s)

$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$

Arc generator

𝑃𝐴𝑇𝐻

\mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 1, 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 2)

𝐿𝑂𝑂𝑃

\mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 1, 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 2)

Arc arity

Arc constraint(s)

• 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 1 . 𝚟𝚊𝚛 \neq 0

• 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 2 . 𝚟𝚊𝚛 \neq 0

Sets

𝖢𝖢 \mapsto [𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜]

Constraint(s) on sets

𝚊𝚖𝚘𝚗𝚐_𝚕𝚘𝚠_𝚞𝚙

(𝙰𝚃𝙻𝙴𝙰𝚂𝚃, 𝙰𝚃𝙼𝙾𝚂𝚃, 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜, 𝚅𝙰𝙻𝚄𝙴𝚂)

Graph model

Note that the arc constraint will produce the different sequences of consecutive variables that do not contain any 0. The $𝖢𝖢$ set generator produces all the connected components of the final graph.

Parts (A) and (B) of Figure 5.349.1 respectively show the initial and final graph associated with the Example slot. Since we use the set generator $𝖢𝖢$ we show the two connected components of the final graph. Since these two connected components both contains between 2 and 3 variables that take their values in ${7, 9}$ the $𝚜𝚕𝚒𝚍𝚒𝚗𝚐_𝚌𝚊𝚛𝚍_𝚜𝚔𝚒𝚙 0$ constraint holds.

Figure 5.349.1. Initial and final graph of the $𝚜𝚕𝚒𝚍𝚒𝚗𝚐_𝚌𝚊𝚛𝚍_𝚜𝚔𝚒𝚙 0$ constraint


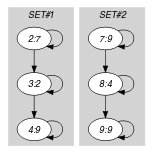
(a)	(b)

Automaton

Figure 5.349.2 depicts the automaton associated with the $𝚜𝚕𝚒𝚍𝚒𝚗𝚐_𝚌𝚊𝚛𝚍_𝚜𝚔𝚒𝚙 0$ constraint. To each variable ${𝚅𝙰𝚁}_{i}$ of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ corresponds a signature variable $S_{i}$ . The following signature constraint links ${𝚅𝙰𝚁}_{i}$ and $S_{i}$ :

$({𝚅𝙰𝚁}_{i} = 0) \Leftrightarrow S_{i} = 0 \land$

$({𝚅𝙰𝚁}_{i} \neq 0 \land {𝚅𝙰𝚁}_{i} \notin 𝚅𝙰𝙻𝚄𝙴𝚂) \Leftrightarrow S_{i} = 1 \land$

$({𝚅𝙰𝚁}_{i} \neq 0 \land {𝚅𝙰𝚁}_{i} \in 𝚅𝙰𝙻𝚄𝙴𝚂) \Leftrightarrow S_{i} = 2$ .

Figure 5.349.2. Automaton of the $𝚜𝚕𝚒𝚍𝚒𝚗𝚐_𝚌𝚊𝚛𝚍_𝚜𝚔𝚒𝚙 0$ constraint

Figure 5.349.3. Hypergraph of the reformulation corresponding to the automaton of the $𝚜𝚕𝚒𝚍𝚒𝚗𝚐_𝚌𝚊𝚛𝚍_𝚜𝚔𝚒𝚙 0$ constraint

Global Constraint Catalog

5. Global Constraint Catalogue

5.349. sliding_card_skip0

Figure 5.349.1. Initial and final graph of the 𝚜𝚕𝚒𝚍𝚒𝚗𝚐_𝚌𝚊𝚛𝚍_𝚜𝚔𝚒𝚙0 constraint

Figure 5.349.2. Automaton of the 𝚜𝚕𝚒𝚍𝚒𝚗𝚐_𝚌𝚊𝚛𝚍_𝚜𝚔𝚒𝚙0 constraint

Figure 5.349.3. Hypergraph of the reformulation corresponding to the automaton of the 𝚜𝚕𝚒𝚍𝚒𝚗𝚐_𝚌𝚊𝚛𝚍_𝚜𝚔𝚒𝚙0 constraint

Figure 5.349.1. Initial and final graph of the $𝚜𝚕𝚒𝚍𝚒𝚗𝚐_𝚌𝚊𝚛𝚍_𝚜𝚔𝚒𝚙 0$ constraint

Figure 5.349.2. Automaton of the $𝚜𝚕𝚒𝚍𝚒𝚗𝚐_𝚌𝚊𝚛𝚍_𝚜𝚔𝚒𝚙 0$ constraint

Figure 5.349.3. Hypergraph of the reformulation corresponding to the automaton of the $𝚜𝚕𝚒𝚍𝚒𝚗𝚐_𝚌𝚊𝚛𝚍_𝚜𝚔𝚒𝚙 0$ constraint