Global Constraint Catalog: Csliding_time_window

5.354. sliding_time_window_sum

DESCRIPTION

LINKS

GRAPH

Origin

Derived from $𝚜𝚕𝚒𝚍𝚒𝚗𝚐_𝚝𝚒𝚖𝚎_𝚠𝚒𝚗𝚍𝚘𝚠$ .

Constraint

$𝚜𝚕𝚒𝚍𝚒𝚗𝚐_𝚝𝚒𝚖𝚎_𝚠𝚒𝚗𝚍𝚘𝚠_𝚜𝚞𝚖 (𝚆𝙸𝙽𝙳𝙾𝚆_𝚂𝙸𝚉𝙴, 𝙻𝙸𝙼𝙸𝚃, 𝚃𝙰𝚂𝙺𝚂)$

Arguments

$𝚆𝙸𝙽𝙳𝙾𝚆_𝚂𝙸𝚉𝙴$	$𝚒𝚗𝚝$
$𝙻𝙸𝙼𝙸𝚃$	$𝚒𝚗𝚝$
$𝚃𝙰𝚂𝙺𝚂$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚘𝚛𝚒𝚐𝚒𝚗 - 𝚍𝚟𝚊𝚛, 𝚎𝚗𝚍 - 𝚍𝚟𝚊𝚛, 𝚗𝚙𝚘𝚒𝚗𝚝 - 𝚍𝚟𝚊𝚛)$

Restrictions

𝚆𝙸𝙽𝙳𝙾𝚆_𝚂𝙸𝚉𝙴 > 0

𝙻𝙸𝙼𝙸𝚃 \geq 0

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚃𝙰𝚂𝙺𝚂, [𝚘𝚛𝚒𝚐𝚒𝚗, 𝚎𝚗𝚍, 𝚗𝚙𝚘𝚒𝚗𝚝])

𝚃𝙰𝚂𝙺𝚂 . 𝚘𝚛𝚒𝚐𝚒𝚗 \leq 𝚃𝙰𝚂𝙺𝚂 . 𝚎𝚗𝚍

𝚃𝙰𝚂𝙺𝚂 . 𝚗𝚙𝚘𝚒𝚗𝚝 \geq 0

Purpose

For any time window of size $𝚆𝙸𝙽𝙳𝙾𝚆_𝚂𝙸𝚉𝙴$ , the sum of the points of the tasks of the collection $𝚃𝙰𝚂𝙺𝚂$ that overlap that time window do not exceed a given limit $𝙻𝙸𝙼𝙸𝚃$ .

Example

(\begin{matrix} 9, 16, 〈\begin{matrix} 𝚘𝚛𝚒𝚐𝚒𝚗 - 10 & 𝚎𝚗𝚍 - 13 & 𝚗𝚙𝚘𝚒𝚗𝚝 - 2, \\ 𝚘𝚛𝚒𝚐𝚒𝚗 - 5 & 𝚎𝚗𝚍 - 6 & 𝚗𝚙𝚘𝚒𝚗𝚝 - 3, \\ 𝚘𝚛𝚒𝚐𝚒𝚗 - 6 & 𝚎𝚗𝚍 - 8 & 𝚗𝚙𝚘𝚒𝚗𝚝 - 4, \\ 𝚘𝚛𝚒𝚐𝚒𝚗 - 14 & 𝚎𝚗𝚍 - 16 & 𝚗𝚙𝚘𝚒𝚗𝚝 - 5, \\ 𝚘𝚛𝚒𝚐𝚒𝚗 - 2 & 𝚎𝚗𝚍 - 4 & 𝚗𝚙𝚘𝚒𝚗𝚝 - 6 \end{matrix}〉 \end{matrix})

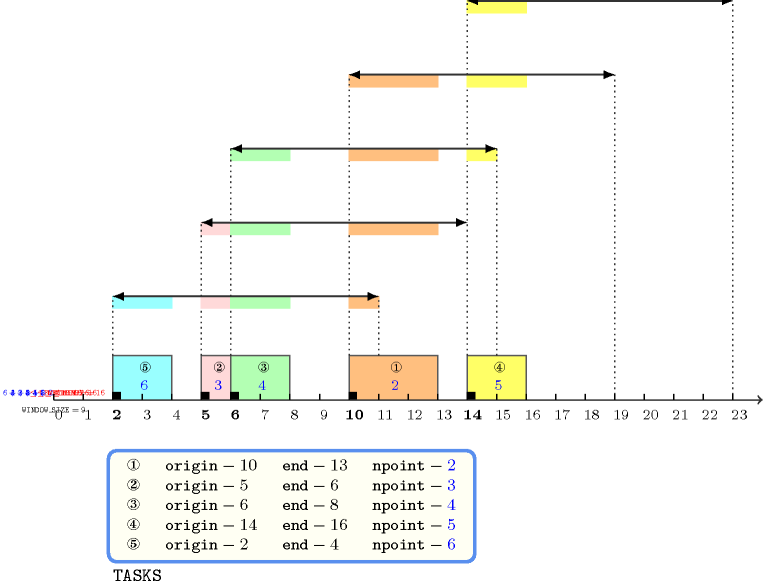
The lower part of Figure 5.354.1 indicates the different tasks on the time axis. Each task is drawn as a rectangle with its corresponding identifier in the middle. Finally the upper part of Figure 5.354.1 shows the different time windows and the respective contribution of the tasks in these time windows. A line with two arrows depicts each time window. The two arrows indicate the start and the end of the time window. At the right of each time window we give its occupation. Since this occupation is always less than or equal to the limit 16, the $𝚜𝚕𝚒𝚍𝚒𝚗𝚐_𝚝𝚒𝚖𝚎_𝚠𝚒𝚗𝚍𝚘𝚠_𝚜𝚞𝚖$ constraint holds.

Figure 5.354.1. Time windows and their use for the five tasks of the Example slot

Typical

𝚆𝙸𝙽𝙳𝙾𝚆_𝚂𝙸𝚉𝙴 > 1

𝙻𝙸𝙼𝙸𝚃 > 0

𝙻𝙸𝙼𝙸𝚃 <

𝚜𝚞𝚖

(𝚃𝙰𝚂𝙺𝚂 . 𝚗𝚙𝚘𝚒𝚗𝚝)

| 𝚃𝙰𝚂𝙺𝚂 | > 1

𝚃𝙰𝚂𝙺𝚂 . 𝚘𝚛𝚒𝚐𝚒𝚗 < 𝚃𝙰𝚂𝙺𝚂 . 𝚎𝚗𝚍

𝚃𝙰𝚂𝙺𝚂 . 𝚗𝚙𝚘𝚒𝚗𝚝 > 0

Symmetries

$𝚆𝙸𝙽𝙳𝙾𝚆_𝚂𝙸𝚉𝙴$ can be decreased.
$𝙻𝙸𝙼𝙸𝚃$ can be increased.
Items of $𝚃𝙰𝚂𝙺𝚂$ are permutable.
$𝚃𝙰𝚂𝙺𝚂 . 𝚗𝚙𝚘𝚒𝚗𝚝$ can be decreased to any value $\geq 0$ .
One and the same constant can be added to the $𝚘𝚛𝚒𝚐𝚒𝚗$ and $𝚎𝚗𝚍$ attributes of all items of $𝚃𝙰𝚂𝙺𝚂$ .

Arg. properties

Contractible wrt. $𝚃𝙰𝚂𝙺𝚂$ .

Usage

This constraint may be used for timetabling problems in order to put an upper limit on the cumulated number of points in a shift.

Reformulation

The $𝚜𝚕𝚒𝚍𝚒𝚗𝚐_𝚝𝚒𝚖𝚎_𝚠𝚒𝚗𝚍𝚘𝚠_𝚜𝚞𝚖$ constraint can be expressed in term of a set of ${| 𝚃𝙰𝚂𝙺𝚂 |}^{2}$ reified constraints and of $| 𝚃𝙰𝚂𝙺𝚂 |$ linear inequalities constraints:

For each pair of tasks $𝚃𝙰𝚂𝙺𝚂 [i], 𝚃𝙰𝚂𝙺𝚂 [j]$ $(i, j \in [1, | 𝚃𝙰𝚂𝙺𝚂 |])$ of the $𝚃𝙰𝚂𝙺𝚂$ collection we create a variable ${𝑃𝑜𝑖𝑛𝑡}_{i j}$ which is set to $𝚃𝙰𝚂𝙺𝚂 [j] . 𝚗𝚙𝚘𝚒𝚗𝚝$ if $𝚃𝙰𝚂𝙺𝚂 [j]$ intersects the time window $𝒲_{i}$ of size $𝚆𝙸𝙽𝙳𝙾𝚆_𝚂𝙸𝚉𝙴$ that starts at instant $𝚃𝙰𝚂𝙺𝚂 [i] . 𝚘𝚛𝚒𝚐𝚒𝚗$ , or 0 otherwise:
- If $i = j$ (i.e., $𝚃𝙰𝚂𝙺𝚂 [i]$ and $𝚃𝙰𝚂𝙺𝚂 [j]$ coincide):
  - ${𝑃𝑜𝑖𝑛𝑡}_{i j} = 𝚃𝙰𝚂𝙺𝚂 [i] . 𝚗𝚙𝚘𝚒𝚗𝚝$ .
- If $i \neq j$ and $\bar{𝚃𝙰𝚂𝙺𝚂 [j] . 𝚎𝚗𝚍} < \underset{̲}{𝚃𝙰𝚂𝙺𝚂 [i] . 𝚘𝚛𝚒𝚐𝚒𝚗}$ (i.e., $𝚃𝙰𝚂𝙺𝚂 [j]$ for sure ends before the time window $𝒲_{i}$ ):
  - ${𝑃𝑜𝑖𝑛𝑡}_{i j} = 0$ .
- If $i \neq j$ and $\underset{̲}{𝚃𝙰𝚂𝙺𝚂 [j] . 𝚘𝚛𝚒𝚐𝚒𝚗} > \bar{𝚃𝙰𝚂𝙺𝚂 [i] . 𝚘𝚛𝚒𝚐𝚒𝚗} + 𝚆𝙸𝙽𝙳𝙾𝚆_𝚂𝙸𝚉𝙴 - 1$ (i.e., $𝚃𝙰𝚂𝙺𝚂 [j]$ for sure starts after the time window $𝒲_{i}$ ):
  - ${𝑃𝑜𝑖𝑛𝑡}_{i j} = 0$ .
- Otherwise (i.e., $𝚃𝙰𝚂𝙺𝚂 [j]$ can potentially overlap the time window $𝒲_{i}$ ):
  - ${𝑃𝑜𝑖𝑛𝑡}_{i j} = min (1, max (0, min (𝚃𝙰𝚂𝙺𝚂 [i] . 𝚘𝚛𝚒𝚐𝚒𝚗 + 𝚆𝙸𝙽𝙳𝙾𝚆_𝚂𝙸𝚉𝙴, 𝚃𝙰𝚂𝙺𝚂 [j] . 𝚎𝚗𝚍) - max (𝚃𝙰𝚂𝙺𝚂 [i] . 𝚘𝚛𝚒𝚐𝚒𝚗, 𝚃𝙰𝚂𝙺𝚂 [j] . 𝚘𝚛𝚒𝚐𝚒𝚗))) \cdot 𝚃𝙰𝚂𝙺𝚂 [j] . 𝚗𝚙𝚘𝚒𝚗𝚝$ .
For each task $𝚃𝙰𝚂𝙺𝚂 [i]$ $(i \in [1, | 𝚃𝙰𝚂𝙺𝚂 |])$ we create a linear inequality constraint ${𝑃𝑜𝑖𝑛𝑡}_{i 1} + {𝑃𝑜𝑖𝑛𝑡}_{i 2} + \dots + {𝑃𝑜𝑖𝑛𝑡}_{i | 𝚃𝙰𝚂𝙺𝚂 |} \leq 𝙻𝙸𝙼𝙸𝚃$ .

See also

related: $𝚜𝚕𝚒𝚍𝚒𝚗𝚐_𝚝𝚒𝚖𝚎_𝚠𝚒𝚗𝚍𝚘𝚠$ (sum of the points of intersecting tasks with sliding time window replaced by sum of intersections of tasks with sliding time window).

used in graph description: $𝚜𝚞𝚖_𝚌𝚝𝚛$ .

Keywords

characteristic of a constraint: time window, sum.

constraint type: sliding sequence constraint, temporal constraint.

Arc input(s)

$𝚃𝙰𝚂𝙺𝚂$

Arc generator

𝑆𝐸𝐿𝐹

\mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚝𝚊𝚜𝚔𝚜)

Arc arity

Arc constraint(s)

𝚝𝚊𝚜𝚔𝚜 . 𝚘𝚛𝚒𝚐𝚒𝚗 \leq 𝚝𝚊𝚜𝚔𝚜 . 𝚎𝚗𝚍

Graph property(ies)

𝐍𝐀𝐑𝐂

= | 𝚃𝙰𝚂𝙺𝚂 |

Arc input(s)

$𝚃𝙰𝚂𝙺𝚂$

Arc generator

𝐶𝐿𝐼𝑄𝑈𝐸

\mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚝𝚊𝚜𝚔𝚜 1, 𝚝𝚊𝚜𝚔𝚜 2)

Arc arity

Arc constraint(s)

• 𝚝𝚊𝚜𝚔𝚜 1 . 𝚎𝚗𝚍 \leq 𝚝𝚊𝚜𝚔𝚜 2 . 𝚎𝚗𝚍

• 𝚝𝚊𝚜𝚔𝚜 2 . 𝚘𝚛𝚒𝚐𝚒𝚗 - 𝚝𝚊𝚜𝚔𝚜 1 . 𝚎𝚗𝚍 < 𝚆𝙸𝙽𝙳𝙾𝚆_𝚂𝙸𝚉𝙴 - 1

Sets

\begin{matrix} 𝖲𝖴𝖢𝖢 \mapsto \\ [\begin{matrix} 𝚜𝚘𝚞𝚛𝚌𝚎, \\ 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 - 𝚌𝚘𝚕 (\begin{matrix} 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 - 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛), \\ 𝚒𝚝𝚎𝚖 (𝚟𝚊𝚛 - 𝚃𝙰𝚂𝙺𝚂 . 𝚗𝚙𝚘𝚒𝚗𝚝)] \end{matrix}) \end{matrix}] \end{matrix}

Constraint(s) on sets

𝚜𝚞𝚖_𝚌𝚝𝚛

(𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜, \leq, 𝙻𝙸𝙼𝙸𝚃)

Graph model

We generate an arc from a task $t_{1}$ to a task $t_{2}$ if task $t_{2}$ does not end before the end of task $t_{1}$ and if task $t_{2}$ intersects the time window that starts at the last instant of task $t_{1}$ . Each set generated by $𝖲𝖴𝖢𝖢$ corresponds to all tasks that intersect in time the time window that starts at instant $𝚎𝚗𝚍 - 1$ , where $𝚎𝚗𝚍$ is the end of a given task.

Parts (A) and (B) of Figure 5.354.2 respectively show the initial and final graph associated with the Example slot. In the final graph, the successors of a given task $t$ correspond to the set of tasks that both do not end before the $𝚎𝚗𝚍$ of task $t$ , and intersect the time window that starts at the $𝚎𝚗𝚍 - 1$ of task $t$ .

Figure 5.354.2. Initial and final graph of the $𝚜𝚕𝚒𝚍𝚒𝚗𝚐_𝚝𝚒𝚖𝚎_𝚠𝚒𝚗𝚍𝚘𝚠_𝚜𝚞𝚖$ constraint


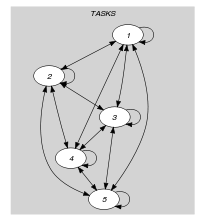
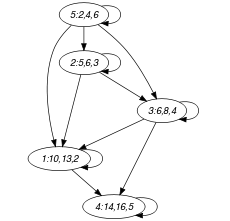
(a)	(b)

Signature

Consider the first graph constraint. Since we use the $𝑆𝐸𝐿𝐹$ arc generator on the $𝚃𝙰𝚂𝙺𝚂$ collection the maximum number of arcs of the final graph is equal to $| 𝚃𝙰𝚂𝙺𝚂 |$ . Therefore we can rewrite $𝐍𝐀𝐑𝐂 = | 𝚃𝙰𝚂𝙺𝚂 |$ to $𝐍𝐀𝐑𝐂 \geq | 𝚃𝙰𝚂𝙺𝚂 |$ and simplify $\underset{̲}{\bar{𝐍𝐀𝐑𝐂}}$ to $\bar{𝐍𝐀𝐑𝐂}$ .

Global Constraint Catalog

5. Global Constraint Catalogue

5.354. sliding_time_window_sum

Figure 5.354.1. Time windows and their use for the five tasks of the Example slot

Figure 5.354.2. Initial and final graph of the 𝚜𝚕𝚒𝚍𝚒𝚗𝚐_𝚝𝚒𝚖𝚎_𝚠𝚒𝚗𝚍𝚘𝚠_𝚜𝚞𝚖 constraint

Figure 5.354.2. Initial and final graph of the $𝚜𝚕𝚒𝚍𝚒𝚗𝚐_𝚝𝚒𝚖𝚎_𝚠𝚒𝚗𝚍𝚘𝚠_𝚜𝚞𝚖$ constraint