5.282. not_all_equal
| DESCRIPTION | LINKS | GRAPH | AUTOMATON |
- Origin
CHIP
- Constraint
- Argument
- Restrictions
- Purpose
The variables of the collection should take more than a single value.
- Example
-
The constraint holds since the collection involves more than one value (i.e., values 1 and 3).
- Typical
- Symmetries
Items of are permutable.
All occurrences of two distinct values of can be swapped; all occurrences of a value of can be renamed to any unused value.
- Arg. properties
Extensible wrt. .
- Algorithm
If the intersection of the domains of the variables of the collection is empty the constraint is entailed. Otherwise, when only a single variable remains not fixed, remove the unique value (unique since the constraint is not entailed) taken by the other variables from the domain of .
- Reformulation
- Counting
-
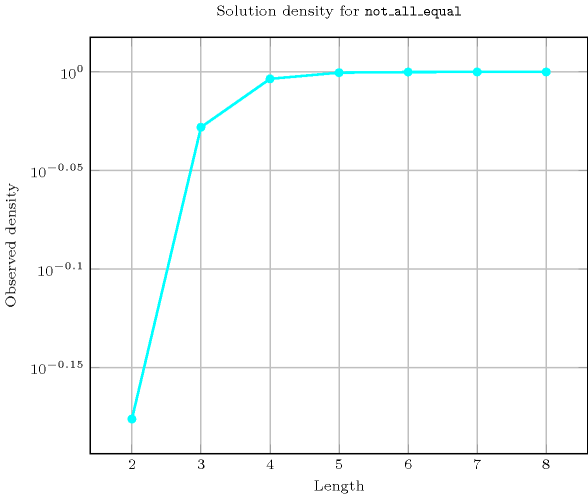
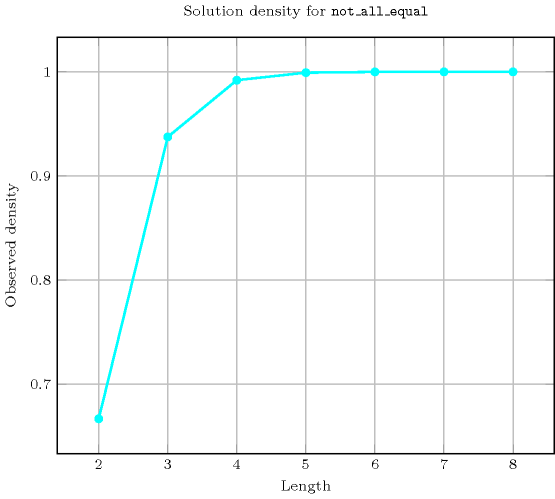
Length () 2 3 4 5 6 7 8 Solutions 6 60 620 7770 117642 2097144 43046712 Number of solutions for : domains
- Systems
- See also
generalisation: (introduce a variable for counting the number of distinct values).
specialisation: (when go down to two variables).
- Keywords
characteristic of a constraint: disequality, automaton, automaton without counters, reified automaton constraint.
constraint network structure: sliding cyclic(1) constraint network(1).
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
- Graph property(ies)
-
- Graph model
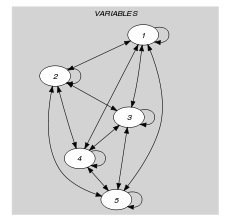
Parts (A) and (B) of Figure 5.282.1 respectively show the initial and final graph associated with the Example slot. Since we use the graph property we show the different strongly connected components of the final graph. Each strongly connected component corresponds to a value that is assigned to some variables of the collection. The holds since the final graph contains more than one strongly connected component.
Figure 5.282.1. Initial and final graph of the constraint
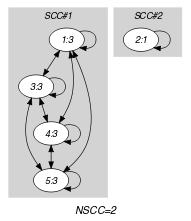
(a) (b)
- Automaton
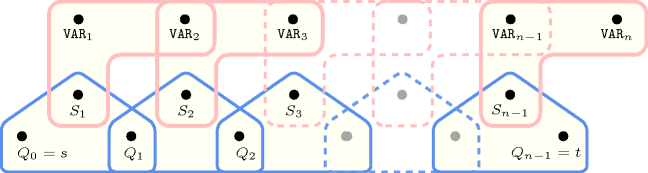
Figure 5.282.2 depicts the automaton associated with the constraint. To each pair of consecutive variables of the collection corresponds a signature variable . The following signature constraint links , and : .
Figure 5.282.2. Automaton of the constraint
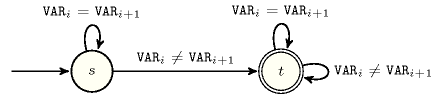
Figure 5.282.3. Hypergraph of the reformulation corresponding to the automaton of the constraint