5.33. arith_sliding
| DESCRIPTION | LINKS | GRAPH | AUTOMATON |
- Origin
Used in the definition of some automaton
- Constraint
- Arguments
- Restrictions
- Purpose
Enforce for all sequences of variables of the collection to have .
- Example
-
The constraint holds since all the following seven inequalities hold:
,
,
,
,
,
,
.
- Typical
- Arg. properties
Contractible wrt. when and .
Suffix-contractible wrt. .
- See also
common keyword: (arithmetic constraint).
implies: .
- Keywords
characteristic of a constraint: hypergraph, automaton, automaton with counters.
combinatorial object: sequence.
constraint type: arithmetic constraint, decomposition, sliding sequence constraint.
- Automaton
Figure 5.33.1 depicts the automaton associated with the constraint. To each item of the collection corresponds a signature variable that is equal to 0.
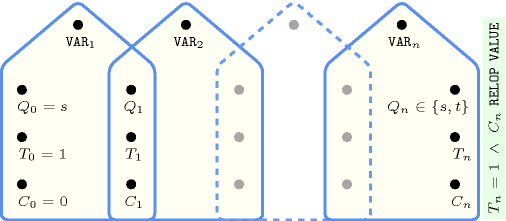
Figure 5.33.1. Automaton of the constraint ( is initially set to 1 and reset to 0 as soon as one of the sliding constraints does not hold)
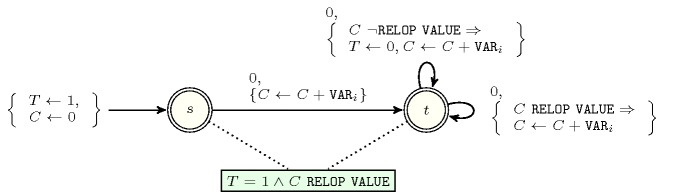
Figure 5.33.2. Hypergraph of the reformulation corresponding to the automaton (with two counters) of the constraint (since all states of the automaton are accepting there is no restriction on the last variable )