Extension of accessibility parameter of $\mathrm{𝚍𝚒𝚏𝚏𝚗}$.

$\mathrm{𝚟𝚒𝚜𝚒𝚋𝚕𝚎}(𝙺,\mathrm{𝙳𝙸𝙼𝚂},\mathrm{𝙵𝚁𝙾𝙼},\mathrm{𝙾𝙱𝙹𝙴𝙲𝚃𝚂},\mathrm{𝚂𝙱𝙾𝚇𝙴𝚂})$

The five previous examples correspond respectively to parts (I), (II) of Figure 5.419.2, to parts (III) and (IV) of Figure 5.419.3, and to Figure 5.419.4. Before introducing these five examples Figure 5.419.1 first illustrates the notion of observations places and of visible faces.

Figure 5.419.1. Entirely visible faces (depicted by a thick line) of rectangles ①, ②, ③, ④, ⑤, ⑥ and ⑦ from the four observation places $\langle \mathrm{𝚍𝚒𝚖}=0,\mathrm{𝚍𝚒𝚛}=1\rangle$, $\langle \mathrm{𝚍𝚒𝚖}=0,\mathrm{𝚍𝚒𝚛}=0\rangle$, $\langle \mathrm{𝚍𝚒𝚖}=1,\mathrm{𝚍𝚒𝚛}=1\rangle$ and $\langle \mathrm{𝚍𝚒𝚖}=1,\mathrm{𝚍𝚒𝚛}=0\rangle$ (depicted by a small triangle)

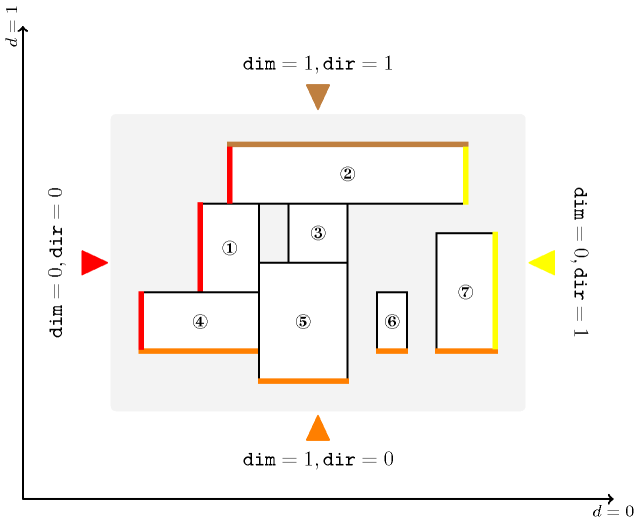
We first need to introduce a number of definitions in order to illustrate the notion of visibility.

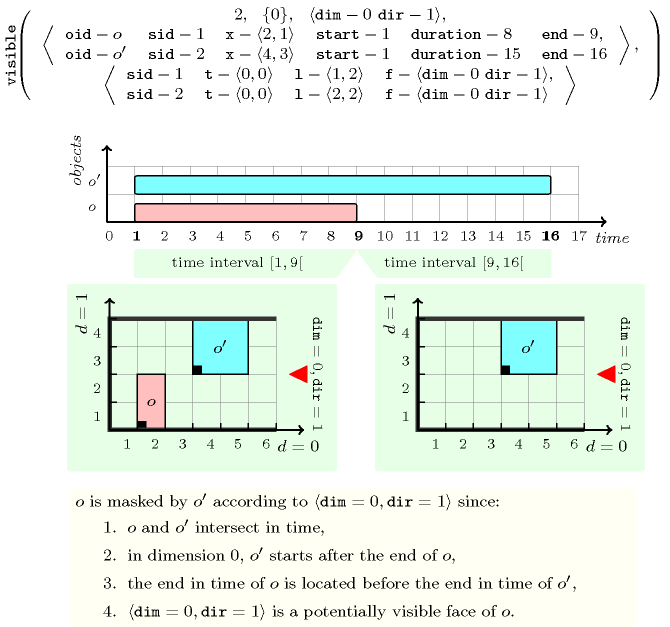
Figures 5.419.2, 5.419.3, and  5.419.4 respectively illustrate Definition Definition 1 in the context of an observation place (depicted by a triangle) that is equal to the pair $\langle \mathrm{𝚍𝚒𝚖}=0,\mathrm{𝚍𝚒𝚛}=1\rangle$. Note that, in the context of Figure 5.419.4, as the $\mathrm{𝙳𝙸𝙼𝚂}$ parameter of the $\mathrm{𝚟𝚒𝚜𝚒𝚋𝚕𝚎}$ constraint only mentions dimension 0 (and not dimension 1), one object may be masked by another object even though the two objects do not intersect in any dimension: i.e., only their respective ordering in the dimension $\mathrm{𝚍𝚒𝚖}=0$ as well as their positions in time matter.

Figure 5.419.2. Illustration of Definition Definition 1: two examples (I) and (II) where an object $o$ is masked by an object $o^{\text{'}}$ according to dimensions $\{0,1\}$ and to the observation place $\langle \mathrm{𝚍𝚒𝚖}=0,\mathrm{𝚍𝚒𝚛}=1\rangle$ because (A) $o$ and $o^{\text{'}}$ intersect in time, (B) $o$ and $o^{\text{'}}$ intersect in dimension 1, (C) $o$ and $o^{\text{'}}$ are not well ordered according to the observation place, (D) there exists an instant where $o^{\text{'}}$ if present (but not $o$) and (E) $\langle \mathrm{𝚍𝚒𝚖}=0,\mathrm{𝚍𝚒𝚛}=1\rangle$ is a potentially visible face of $o$.

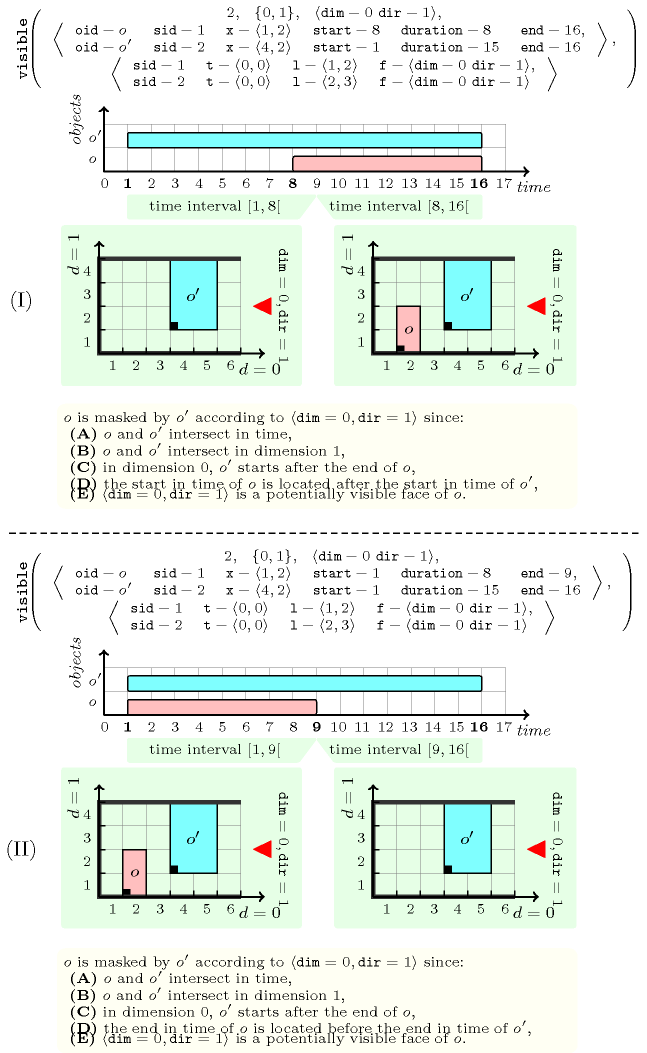
Figure 5.419.3. Illustration of Definition Definition 1: two examples (III) and (IV) where an object $o$ is not masked by an object $o^{\text{'}}$ according to the observation place $\langle \mathrm{𝚍𝚒𝚖}=0,\mathrm{𝚍𝚒𝚛}=1\rangle$.

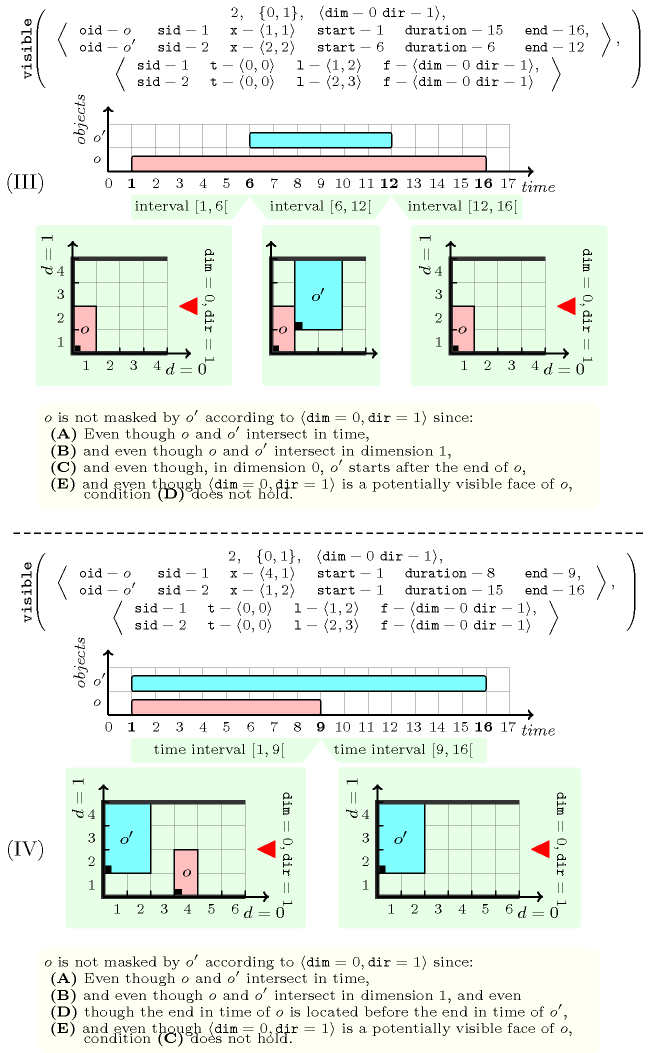
Figure 5.419.4. Illustration of Definition Definition 1: the case where an object $o$ is masked by an object $o^{\text{'}}$ according to dimension 0 and to the observation place $\langle \mathrm{𝚍𝚒𝚖}=0,\mathrm{𝚍𝚒𝚛}=1\rangle$ because: (A) $o$ and $o^{\text{'}}$ intersect in time, (C) $o$ and $o^{\text{'}}$ are not well ordered according to the observation place and (D) there exists an instant where $o^{\text{'}}$ if present (but not $o$) and (E) $\langle \mathrm{𝚍𝚒𝚖}=0,\mathrm{𝚍𝚒𝚛}=1\rangle$ is a potentially visible face of $o$.

We are now in position to define the $\mathrm{𝚟𝚒𝚜𝚒𝚋𝚕𝚎}$ constraint.

• Items of $\mathrm{𝙾𝙱𝙹𝙴𝙲𝚃𝚂}$ are permutable.

• Items of $\mathrm{𝚂𝙱𝙾𝚇𝙴𝚂}$ are permutable.

We now give several typical concrete uses of the $\mathrm{𝚟𝚒𝚜𝚒𝚋𝚕𝚎}$ constraint, which all mention the $\mathrm{𝚍𝚒𝚏𝚏𝚜𝚝}$ as well as the $\mathrm{𝚟𝚒𝚜𝚒𝚋𝚕𝚎}$ constraints:

• Figure 5.419.5 corresponds to a ship loading problem where containers are piled within a ship by a crane each time the ship visits a given harbour. In this context we have first to express the fact that a container can only be placed on top of an already placed container and second, that a container can only be taken away if no container is placed on top of it. These two conditions are expressed by a single $\mathrm{𝚟𝚒𝚜𝚒𝚋𝚕𝚎}$ constraint for which the $\mathrm{𝙳𝙸𝙼𝚂}$ parameter mentions all three dimensions of the placement space and the $\mathrm{𝙵𝚁𝙾𝙼}$ parameter mentions the pair $\langle \mathrm{𝚍𝚒𝚖}=2,\mathrm{𝚍𝚒𝚛}=1\rangle$ as its unique observation place. In addition we also use a $\mathrm{𝚍𝚒𝚏𝚏𝚜𝚝}$ constraint for expressing non-overlapping.

  Figure 5.419.5. Illustration of the ship loading problem

  

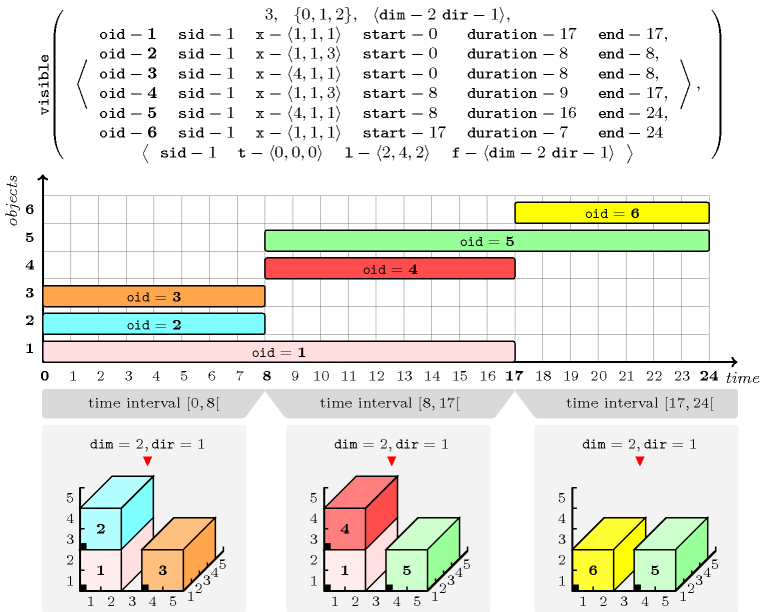
• Figure 5.419.6 corresponds to a container loading/unloading problem in the context of a pick-up delivery problem where the loading/unloading takes place with respect to the front door of the container. Beside the $\mathrm{𝚍𝚒𝚏𝚏𝚜𝚝}$ constraint used for expressing non-overlapping, we use two distinct $\mathrm{𝚟𝚒𝚜𝚒𝚋𝚕𝚎}$ constraints:

  • The first $\mathrm{𝚟𝚒𝚜𝚒𝚋𝚕𝚎}$ constraint takes care of the location of the front door of the container (each object $o$ has to be loaded/unloaded without moving around any other object, i.e., objects that are in the vis-à-vis of $o$ according to the front door of the container). This is expressed by a single $\mathrm{𝚟𝚒𝚜𝚒𝚋𝚕𝚎}$ constraint for which the $\mathrm{𝙳𝙸𝙼𝚂}$ parameter mentions all three dimensions of the placement space and the $\mathrm{𝙵𝚁𝙾𝙼}$ parameter mentions the pair $\langle \mathrm{𝚍𝚒𝚖}=1,\mathrm{𝚍𝚒𝚛}=0\rangle$ as its unique observation place.

  • The second $\mathrm{𝚟𝚒𝚜𝚒𝚋𝚕𝚎}$ constraint takes care of the gravity dimension (i.e., each object that has to be loaded should not be put under another object, and reciprocally each object that has to be unloaded should not be located under another object). This is expressed by the same $\mathrm{𝚟𝚒𝚜𝚒𝚋𝚕𝚎}$ constraint that was used for the ship loading problem, i.e., a $\mathrm{𝚟𝚒𝚜𝚒𝚋𝚕𝚎}$ constraint for which the $\mathrm{𝙳𝙸𝙼𝚂}$ parameter mentions all three dimensions of the placement space and the $\mathrm{𝙵𝚁𝙾𝙼}$ parameter mentions the pair $\langle \mathrm{𝚍𝚒𝚖}=2,\mathrm{𝚍𝚒𝚛}=1\rangle$ as its unique observation place.

  Figure 5.419.6. Illustration of the pick-up delivery problem

  

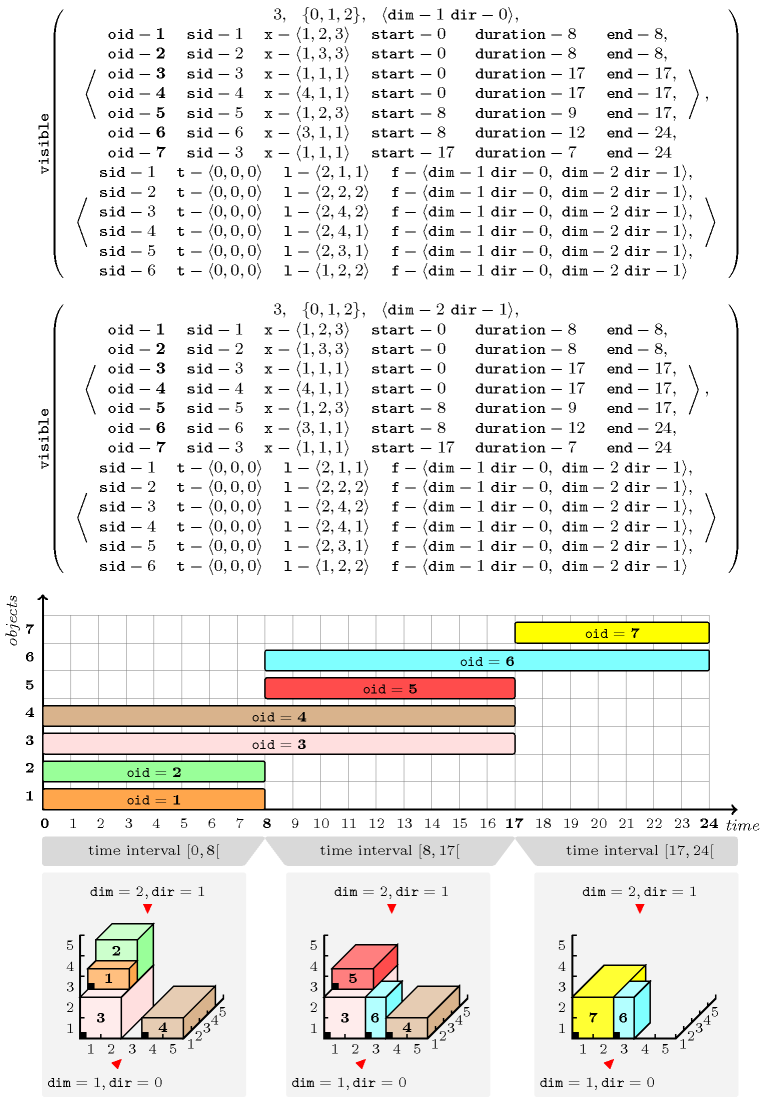
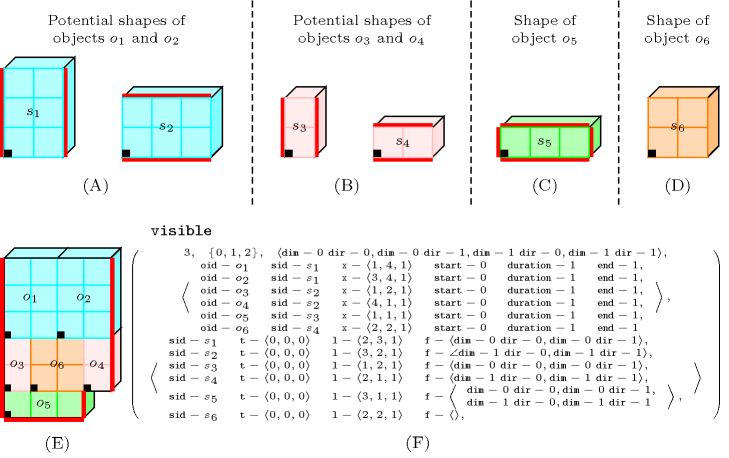
• Figure 5.419.7 corresponds to a pallet loading problem where one has to place six objects on a pallet. Each object corresponds to a parallelepiped that has a bar code on one of its four sides (i.e., the sides that are different from the top and the bottom of the parallelepiped). If, for some reason, an object has no bar code then we simply remove it from the objects that will be passed to the $\mathrm{𝚟𝚒𝚜𝚒𝚋𝚕𝚎}$ constraint: this is for instance the case for the sixth object. In this context the constraint to enforce (beside the non-overlapping constraint between the parallelepipeds that are assigned to a same pallet) is the fact that the bar code of each object should be visible (i.e., visible from one of the four sides of the pallet). This is expressed by the $\mathrm{𝚟𝚒𝚜𝚒𝚋𝚕𝚎}$ constraint given in Part (F) of Figure 5.419.7.

Figure 5.419.7. Illustration of the pallet loading problem

The $\mathrm{𝚟𝚒𝚜𝚒𝚋𝚕𝚎}$ constraint is a generalisation of the $\mathrm{𝚊𝚌𝚌𝚎𝚜𝚜𝚒𝚋𝚒𝚕𝚒𝚝𝚢}$ constraint initially introduced in the context of the $\mathrm{𝚍𝚒𝚏𝚏𝚗}$ constraint.

common keyword: $\mathrm{𝚍𝚒𝚏𝚏𝚗}$ (geometrical constraint),

$\mathrm{𝚐𝚎𝚘𝚜𝚝}$, $\mathrm{𝚐𝚎𝚘𝚜𝚝}\_\mathrm{𝚝𝚒𝚖𝚎}$ (geometrical constraint,sweep),

$\mathrm{𝚗𝚘𝚗}\_\mathrm{𝚘𝚟𝚎𝚛𝚕𝚊𝚙}\_\mathrm{𝚜𝚋𝚘𝚡𝚎𝚜}$ (geometrical constraint).

constraint type: decomposition, predefined constraint.

filtering: sweep.

geometry: geometrical constraint.