Global Constraint Catalog: Csum

5.384. sum_ctr

DESCRIPTION

LINKS

GRAPH

Origin

Arithmetic constraint.

Constraint

$𝚜𝚞𝚖_𝚌𝚝𝚛 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝙲𝚃𝚁, 𝚅𝙰𝚁)$

Synonyms

$𝚌𝚘𝚗𝚜𝚝𝚊𝚗𝚝_𝚜𝚞𝚖$ , $𝚜𝚞𝚖$ , $𝚕𝚒𝚗𝚎𝚊𝚛$ , $𝚜𝚌𝚊𝚕𝚊𝚛_𝚙𝚛𝚘𝚍𝚞𝚌𝚝$ .

Arguments

$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛)$
$𝙲𝚃𝚁$	$𝚊𝚝𝚘𝚖$
$𝚅𝙰𝚁$	$𝚍𝚟𝚊𝚛$

Restrictions

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚟𝚊𝚛)

𝙲𝚃𝚁 \in [=, \neq, <, \geq, >, \leq]

Purpose

Constraint the sum of a set of domain variables. More precisely, let $𝚂$ denote the sum of the variables of the $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ collection (when the collection is empty the corresponding sum is equal to 0). Enforce the following constraint to hold: $𝚂 𝙲𝚃𝚁 𝚅𝙰𝚁$ .

Example

(〈1, 1, 4〉, =, 6)

The $𝚜𝚞𝚖_𝚌𝚝𝚛$ constraint holds since the condition $1 + 1 + 4 = 6$ is satisfied.

Typical

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | > 1

𝚛𝚊𝚗𝚐𝚎

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛) > 1

𝙲𝚃𝚁 \in [=, <, \geq, >, \leq]

Symmetry

Items of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ are permutable.

Arg. properties

Contractible wrt. $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ when $𝙲𝚃𝚁 \in [<, \leq]$ and $𝚖𝚒𝚗𝚟𝚊𝚕 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛) \geq 0$ .
Contractible wrt. $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ when $𝙲𝚃𝚁 \in [\geq, >]$ and $𝚖𝚊𝚡𝚟𝚊𝚕 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛) \leq 0$ .
Extensible wrt. $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ when $𝙲𝚃𝚁 \in [\geq, >]$ and $𝚖𝚒𝚗𝚟𝚊𝚕 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛) \geq 0$ .
Extensible wrt. $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ when $𝙲𝚃𝚁 \in [<, \leq]$ and $𝚖𝚊𝚡𝚟𝚊𝚕 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛) \leq 0$ .
Aggregate: $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 (𝚞𝚗𝚒𝚘𝚗)$ , $𝙲𝚃𝚁 (𝚒𝚍)$ , $𝚅𝙰𝚁 (+)$ .

Remark

When $𝙲𝚃𝚁$ corresponds to $=$ this constraint is referenced under the names $𝚌𝚘𝚗𝚜𝚝𝚊𝚗𝚝_𝚜𝚞𝚖$ in KOALOG (http://www.koalog.com/php/index.php) and $𝚜𝚞𝚖$ in JaCoP (http://www.jacop.eu/).

Systems

equation in Choco, linear in Gecode, scalar_product in SICStus.

Used in

$𝚋𝚒𝚗_𝚙𝚊𝚌𝚔𝚒𝚗𝚐$ , $𝚌𝚞𝚖𝚞𝚕𝚊𝚝𝚒𝚟𝚎$ , $𝚌𝚞𝚖𝚞𝚕𝚊𝚝𝚒𝚟𝚎_𝚌𝚘𝚗𝚟𝚎𝚡$ , $𝚌𝚞𝚖𝚞𝚕𝚊𝚝𝚒𝚟𝚎_𝚠𝚒𝚝𝚑_𝚕𝚎𝚟𝚎𝚕_𝚘𝚏_𝚙𝚛𝚒𝚘𝚛𝚒𝚝𝚢$ , $𝚌𝚞𝚖𝚞𝚕𝚊𝚝𝚒𝚟𝚎𝚜$ , $𝚒𝚗𝚍𝚎𝚡𝚎𝚍_𝚜𝚞𝚖$ , $𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕_𝚊𝚗𝚍_𝚜𝚞𝚖$ , $𝚛𝚎𝚕𝚊𝚡𝚎𝚍_𝚜𝚕𝚒𝚍𝚒𝚗𝚐_𝚜𝚞𝚖$ , $𝚜𝚕𝚒𝚍𝚒𝚗𝚐_𝚜𝚞𝚖$ , $𝚜𝚕𝚒𝚍𝚒𝚗𝚐_𝚝𝚒𝚖𝚎_𝚠𝚒𝚗𝚍𝚘𝚠_𝚜𝚞𝚖$ .

common keyword: $𝚊𝚛𝚒𝚝𝚑_𝚜𝚕𝚒𝚍𝚒𝚗𝚐$ (arithmetic constraint), $𝚒𝚗𝚌𝚛𝚎𝚊𝚜𝚒𝚗𝚐_𝚜𝚞𝚖$ (sum), $𝚙𝚛𝚘𝚍𝚞𝚌𝚝_𝚌𝚝𝚛$ , $𝚛𝚊𝚗𝚐𝚎_𝚌𝚝𝚛$ (arithmetic constraint), $𝚜𝚞𝚖$ , $𝚜𝚞𝚖_𝚌𝚞𝚋𝚎𝚜_𝚌𝚝𝚛$ , $𝚜𝚞𝚖_𝚙𝚘𝚠𝚎𝚛𝚜 4_𝚌𝚝𝚛$ , $𝚜𝚞𝚖_𝚙𝚘𝚠𝚎𝚛𝚜 5_𝚌𝚝𝚛$ , $𝚜𝚞𝚖_𝚙𝚘𝚠𝚎𝚛𝚜 6_𝚌𝚝𝚛$ (sum), $𝚜𝚞𝚖_𝚜𝚎𝚝$ (arithmetic constraint), $𝚜𝚞𝚖_𝚜𝚚𝚞𝚊𝚛𝚎𝚜_𝚌𝚝𝚛$ (sum).

generalisation: $𝚜𝚌𝚊𝚕𝚊𝚛_𝚙𝚛𝚘𝚍𝚞𝚌𝚝$ (arithmetic constraint where all coefficients are not necessarly equal to 1).

implied by: $𝚊𝚛𝚒𝚝𝚑_𝚜𝚕𝚒𝚍𝚒𝚗𝚐$ .

system of constraints: $𝚜𝚕𝚒𝚍𝚒𝚗𝚐_𝚜𝚞𝚖$ .

Keywords

characteristic of a constraint: sum.

constraint type: arithmetic constraint.

heuristics: regret based heuristics, regret based heuristics in matrix problems.

Cond. implications

$•$ $𝚜𝚞𝚖_𝚌𝚝𝚛 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝙲𝚃𝚁, 𝚅𝙰𝚁)$

with $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛 \geq 0$

and $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛 \leq 1$

implies $𝚜𝚞𝚖_𝚜𝚚𝚞𝚊𝚛𝚎𝚜_𝚌𝚝𝚛$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝙲𝚃𝚁, 𝚅𝙰𝚁)$

when $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛 \geq 0$

and $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛 \leq 1$ .

$•$ $𝚜𝚞𝚖_𝚌𝚝𝚛 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝙲𝚃𝚁, 𝚅𝙰𝚁)$

with $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛 \geq - 1$

and $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛 \leq 1$

implies $𝚜𝚞𝚖_𝚌𝚞𝚋𝚎𝚜_𝚌𝚝𝚛$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝙲𝚃𝚁, 𝚅𝙰𝚁)$

when $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛 \geq - 1$

and $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛 \leq 1$ .

$•$ $𝚜𝚞𝚖_𝚌𝚝𝚛 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝙲𝚃𝚁, 𝚅𝙰𝚁)$

with $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛 \geq - 1$

and $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛 \leq 1$

implies $𝚜𝚞𝚖_𝚙𝚘𝚠𝚎𝚛𝚜 5_𝚌𝚝𝚛$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝙲𝚃𝚁, 𝚅𝙰𝚁)$

when $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛 \geq - 1$

and $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛 \leq 1$ .

$•$ $𝚜𝚞𝚖_𝚌𝚝𝚛 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝙲𝚃𝚁, 𝚅𝙰𝚁)$

with $𝙲𝚃𝚁 \in [=]$

and $𝚒𝚗𝚌𝚛𝚎𝚊𝚜𝚒𝚗𝚐$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

implies $𝚒𝚗𝚌𝚛𝚎𝚊𝚜𝚒𝚗𝚐_𝚜𝚞𝚖$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚅𝙰𝚁)$ .

Arc input(s)

$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$

Arc generator

𝑆𝐸𝐿𝐹

\mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜)

Arc arity

Arc constraint(s)

𝚃𝚁𝚄𝙴

Graph property(ies)

𝐒𝐔𝐌

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚟𝚊𝚛) 𝙲𝚃𝚁 𝚅𝙰𝚁

Graph model

Since we want to keep all the vertices of the initial graph we use the $𝑆𝐸𝐿𝐹$ arc generator together with the $𝚃𝚁𝚄𝙴$ arc constraint. This predefined arc constraint always holds.

Parts (A) and (B) of Figure 5.384.1 respectively show the initial and final graph associated with the Example slot. Since we use the $𝚃𝚁𝚄𝙴$ arc constraint both graphs are identical.

Figure 5.384.1. Initial and final graph of the $𝚜𝚞𝚖_𝚌𝚝𝚛$ constraint


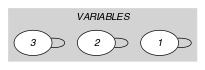
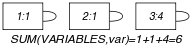
(a)	(b)

Global Constraint Catalog

5. Global Constraint Catalogue

5.384. sum_ctr

Figure 5.384.1. Initial and final graph of the 𝚜𝚞𝚖_𝚌𝚝𝚛 constraint

Figure 5.384.1. Initial and final graph of the $𝚜𝚞𝚖_𝚌𝚝𝚛$ constraint