Global Constraint Catalog: Cmin

5.257. min_nvalue

DESCRIPTION

LINKS

GRAPH

AUTOMATON

Origin

N. Beldiceanu

Constraint

$𝚖𝚒𝚗_𝚗𝚟𝚊𝚕𝚞𝚎 (𝙼𝙸𝙽, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

Arguments

$𝙼𝙸𝙽$	$𝚍𝚟𝚊𝚛$
$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛)$

Restrictions

𝙼𝙸𝙽 \geq 1

𝙼𝙸𝙽 \leq | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 |

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚟𝚊𝚛)

Purpose

$𝙼𝙸𝙽$ is the minimum number of times that the same value is taken by the variables of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ .

Example

(2, 〈9, 1, 7, 1, 1, 7, 7, 7, 7, 9〉)

(5, 〈8, 8, 8, 8, 8〉)

(2, 〈1, 8, 1, 8, 1〉)

In the first example, values $1, 7, 9$ are respectively used $3, 5, 2$ times. So the minimum number of time $𝙼𝙸𝙽$ that a same value occurs is 2. Consequently the corresponding $𝚖𝚒𝚗_𝚗𝚟𝚊𝚕𝚞𝚎$ constraint holds.

Typical

2 * 𝙼𝙸𝙽 \leq | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 |

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | > 1

𝚛𝚊𝚗𝚐𝚎

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛) > 1

Symmetries

Items of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ are permutable.
All occurrences of two distinct values of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛$ can be swapped; all occurrences of a value of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛$ can be renamed to any unused value.

Arg. properties

Functional dependency: $𝙼𝙸𝙽$ determined by $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ .

Usage

This constraint may be used in order to replace a set of $𝚌𝚘𝚞𝚗𝚝$ or $𝚊𝚖𝚘𝚗𝚐$ constraints were one would have to generate explicitly one constraint for each potential value. Also useful for constraining the number of occurrences of the less used value without knowing this value in advance and without giving explicitly a lower limit on the number of occurrences of each value as it is done in the $𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢$ constraint.

Reformulation

Assume that $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ is not empty. Let $α$ and $β$ respectively denote the smallest and largest possible values that can be assigned to the variables of the $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ collection. Let the variables $O_{α}, O_{α + 1}, \dots, O_{β}$ respectively correspond to the number of occurrences of values $α, α + 1, \dots, β$ within the variables of the $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ collection. The $𝚖𝚒𝚗_𝚗𝚟𝚊𝚕𝚞𝚎$ constraint can be expressed as the conjunction of the following two constraints:

$𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂,$

$〈 𝚟𝚊𝚕 - α 𝚗𝚘𝚌𝚌𝚞𝚛𝚛𝚎𝚗𝚌𝚎 - O_{α},$

$𝚟𝚊𝚕 - α + 1 𝚗𝚘𝚌𝚌𝚞𝚛𝚛𝚎𝚗𝚌𝚎 - O_{α + 1},$

$\dots$

$𝚟𝚊𝚕 - β 𝚗𝚘𝚌𝚌𝚞𝚛𝚛𝚎𝚗𝚌𝚎 - O_{β} 〉)$ ,

$𝚖𝚒𝚗_𝚗$ $(𝙼𝙸𝙽, 1, 〈 0, O_{α}, O_{α + 1}, \dots, O_{β} 〉)$ .

We use a $𝚖𝚒𝚗_𝚗$ constraint (with its $𝚁𝙰𝙽𝙺$ parameter set to 1) instead of a $𝚖𝚒𝚗𝚒𝚖𝚞𝚖$ constraint in order to discard the smallest value 0.

Counting

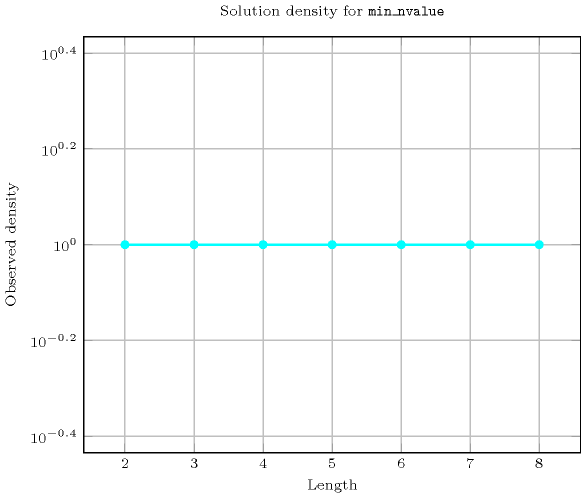
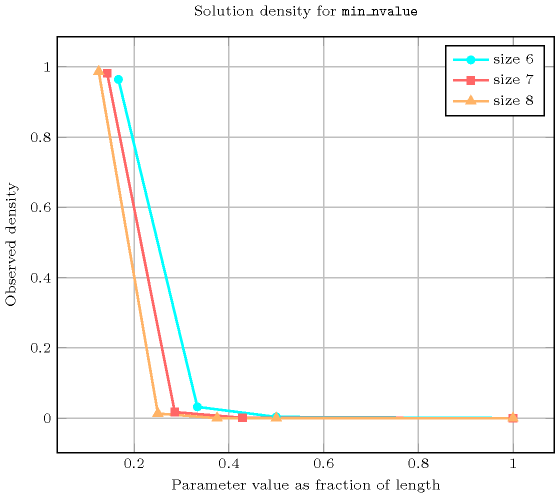
Length ( $n$ )	2	3	4	5	6	7	8
Solutions	9	64	625	7776	117649	2097152	43046721

Number of solutions for $𝚖𝚒𝚗_𝚗𝚟𝚊𝚕𝚞𝚎$ : domains $0 . . n$

ctrs/min_nvalue-1-tikz

ctrs/min_nvalue-2-tikz

Length (

n

)

Total

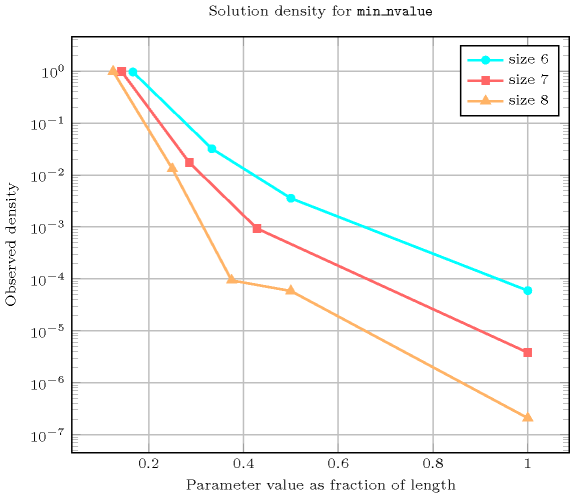
625

7776

117649

2097152

43046721

Parameter

value

560

7470

113442

2058728

42473664

300

3780

36456

566496

420

1960

4032

2520

Solution count for $𝚖𝚒𝚗_𝚗𝚟𝚊𝚕𝚞𝚎$ : domains $0 . . n$

ctrs/min_nvalue-3-tikz

ctrs/min_nvalue-4-tikz

Keywords

application area: assignment.

characteristic of a constraint: minimum, automaton, automaton with array of counters.

constraint arguments: pure functional dependency.

constraint type: value constraint, counting constraint.

final graph structure: equivalence.

modelling: minimum number of occurrences, functional dependency.

Cond. implications

$𝚖𝚒𝚗_𝚗𝚟𝚊𝚕𝚞𝚎 (𝙼𝙸𝙽, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

with $𝙼𝙸𝙽 < | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 |$

implies $𝚊𝚝𝚕𝚎𝚊𝚜𝚝_𝚗𝚟𝚊𝚕𝚞𝚎$ $(𝙽𝚅𝙰𝙻, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

when $𝙽𝚅𝙰𝙻 = 2$ .

Arc input(s)

$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$

Arc generator

𝐶𝐿𝐼𝑄𝑈𝐸

\mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 1, 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 2)

Arc arity

Arc constraint(s)

𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 1 . 𝚟𝚊𝚛 = 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 2 . 𝚟𝚊𝚛

Graph property(ies)

𝐌𝐈𝐍_𝐍𝐒𝐂𝐂

= 𝙼𝙸𝙽

Graph model

Parts (A) and (B) of Figure 5.257.1 respectively show the initial and final graph associated with the first example of the Example slot. Since we use the $𝐌𝐈𝐍_𝐍𝐒𝐂𝐂$ graph property, we show the smallest strongly connected component of the final graph associated with the first example of the Example slot.

Figure 5.257.1. Initial and final graph of the $𝚖𝚒𝚗_𝚗𝚟𝚊𝚕𝚞𝚎$ constraint

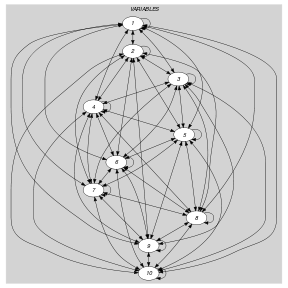
(a)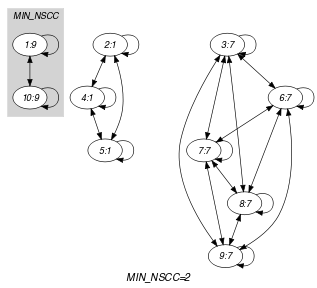

(b)

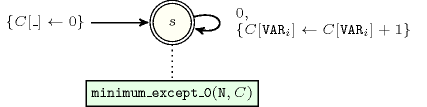
Automaton: Figure 5.257.2 depicts the automaton associated with the $𝚖𝚒𝚗_𝚗𝚟𝚊𝚕𝚞𝚎$ constraint. To each item of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ corresponds a signature variable $S_{i}$ that is equal to 0.

Figure 5.257.2. Automaton of the $𝚖𝚒𝚗_𝚗𝚟𝚊𝚕𝚞𝚎$ constraint

Global Constraint Catalog

5. Global Constraint Catalogue

5.257. min_nvalue

Figure 5.257.1. Initial and final graph of the $𝚖𝚒𝚗_𝚗𝚟𝚊𝚕𝚞𝚎$ constraint

Figure 5.257.2. Automaton of the $𝚖𝚒𝚗_𝚗𝚟𝚊𝚕𝚞𝚎$ constraint

Global Constraint Catalog

5. Global Constraint Catalogue

5.257. min_nvalue

Figure 5.257.1. Initial and final graph of the 𝚖𝚒𝚗_𝚗𝚟𝚊𝚕𝚞𝚎 constraint

Figure 5.257.2. Automaton of the 𝚖𝚒𝚗_𝚗𝚟𝚊𝚕𝚞𝚎 constraint

Figure 5.257.1. Initial and final graph of the $𝚖𝚒𝚗_𝚗𝚟𝚊𝚕𝚞𝚎$ constraint

Figure 5.257.2. Automaton of the $𝚖𝚒𝚗_𝚗𝚟𝚊𝚕𝚞𝚎$ constraint