Global Constraint Catalog: Cmin_width

5.260. min_width_peak

DESCRIPTION

LINKS

AUTOMATON

Origin

derived from $𝚙𝚎𝚊𝚔$

Constraint

$𝚖𝚒𝚗_𝚠𝚒𝚍𝚝𝚑_𝚙𝚎𝚊𝚔 (𝙼𝙸𝙽_𝚆𝙸𝙳𝚃𝙷, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

Synonym

$𝚖𝚒𝚗_𝚋𝚊𝚜𝚎_𝚙𝚎𝚊𝚔$ .

Arguments

$𝙼𝙸𝙽_𝚆𝙸𝙳𝚃𝙷$	$𝚍𝚟𝚊𝚛$
$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛)$

Restrictions

𝙼𝙸𝙽_𝚆𝙸𝙳𝚃𝙷 \geq 0

𝙼𝙸𝙽_𝚆𝙸𝙳𝚃𝙷 \leq | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | - 2

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚟𝚊𝚛)

Purpose

Given a sequence $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ constraint $𝙼𝙸𝙽_𝚆𝙸𝙳𝚃𝙷$ to be fixed to the width of the smallest peak, or to 0 if no peak exists.

Example

(5, 〈4, 4, 2, 2, 3, 5, 5, 6, 3, 1, 1, 2, 2, 2, 2, 2, 2, 1〉)

(5, 〈4, 6, 7, 9, 8, 5, 4〉)

(0, 〈4, 4, 2, 0, 0, 4, 5〉)

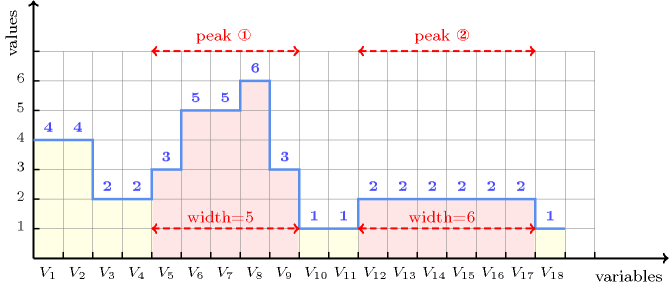
The first $𝚖𝚒𝚗_𝚠𝚒𝚍𝚝𝚑_𝚙𝚎𝚊𝚔$ constraint holds since the sequence $442235563112222221$ contains two peaks of respective width 5 and 6 (see Figure 5.260.1) and since its argument $𝙼𝙸𝙽_𝚆𝙸𝙳𝚃𝙷$ is fixed to the smallest value 5.

Figure 5.260.1. Illustration of the first example of the Example slot: a sequence of eighteen variables $V_{1}$ , $V_{2}$ , $V_{3}$ , $V_{4}$ , $V_{5}$ , $V_{6}$ , $V_{7}$ , $V_{8}$ , $V_{9}$ , $V_{10}$ , $V_{11}$ , $V_{12}$ , $V_{13}$ , $V_{14}$ , $V_{15}$ , $V_{16}$ , $V_{17}$ , $V_{18}$ respectively fixed to values 4, 4, 2, 2, 3, 5, 5, 6, 3, 1, 1, 2, 2, 2, 2, 2, 2, 1 and its two peaks of width 5 and 6.

Typical

𝙼𝙸𝙽_𝚆𝙸𝙳𝚃𝙷 > 1

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | > 2

Symmetries

Items of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ can be reversed.
One and the same constant can be added to the $𝚟𝚊𝚛$ attribute of all items of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ .

Arg. properties

Functional dependency: $𝙼𝙸𝙽_𝚆𝙸𝙳𝚃𝙷$ determined by $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ .

Counting

Length ( $n$ )	2	3	4	5	6	7	8
Solutions	9	64	625	7776	117649	2097152	43046721

Number of solutions for $𝚖𝚒𝚗_𝚠𝚒𝚍𝚝𝚑_𝚙𝚎𝚊𝚔$ : domains $0 . . n$

ctrs/min_width_peak-2-tikz

ctrs/min_width_peak-3-tikz

Length (

n

)

Total

625

7776

117649

2097152

43046721

Parameter

value

295

1792

11088

69498

439791

230

3205

56637

1174398

26327058

100

2100

28420

424928

9363060

679

17024

268722

3413256

4480

130452

2345982

29154

968946

188628

Solution count for $𝚖𝚒𝚗_𝚠𝚒𝚍𝚝𝚑_𝚙𝚎𝚊𝚔$ : domains $0 . . n$

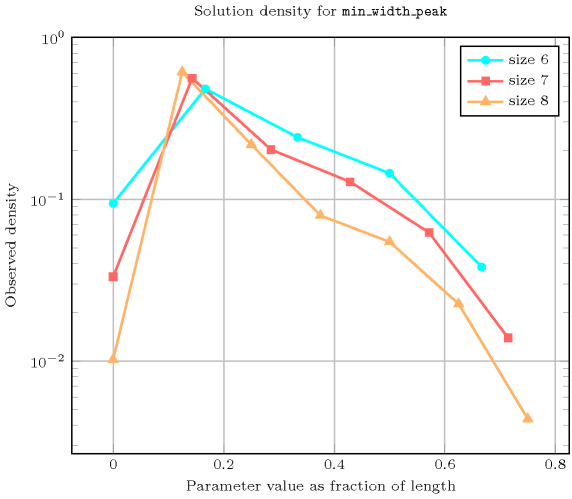
ctrs/min_width_peak-4-tikz

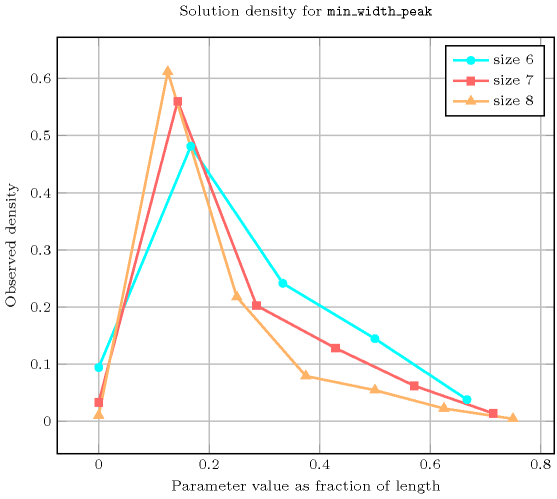
ctrs/min_width_peak-5-tikz

Keywords

characteristic of a constraint: automaton, automaton with counters, automaton with same input symbol.

combinatorial object: sequence.

constraint arguments: reverse of a constraint, pure functional dependency.

filtering: glue matrix.

modelling: functional dependency.

Automaton

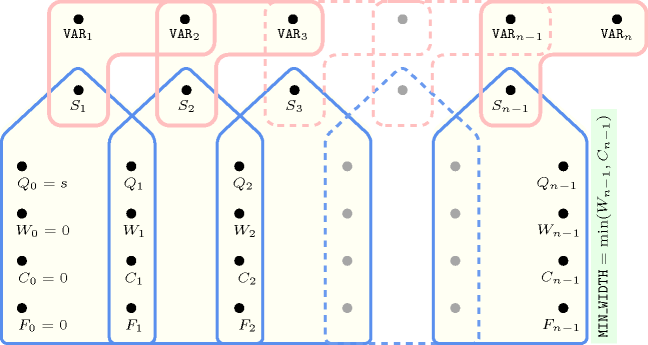
Figure 5.260.2 depicts the automaton associated with the $𝚖𝚒𝚗_𝚠𝚒𝚍𝚝𝚑_𝚙𝚎𝚊𝚔$ constraint. To each pair of consecutive variables $({𝚅𝙰𝚁}_{i}, {𝚅𝙰𝚁}_{i + 1})$ of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ corresponds a signature variable $S_{i}$ . The following signature constraint links ${𝚅𝙰𝚁}_{i}$ , ${𝚅𝙰𝚁}_{i + 1}$ and $S_{i}$ : $({𝚅𝙰𝚁}_{i} < {𝚅𝙰𝚁}_{i + 1} \Leftrightarrow S_{i} = 0) \land ({𝚅𝙰𝚁}_{i} = {𝚅𝙰𝚁}_{i + 1} \Leftrightarrow S_{i} = 1) \land ({𝚅𝙰𝚁}_{i} > {𝚅𝙰𝚁}_{i + 1} \Leftrightarrow S_{i} = 2)$ .

Figure 5.260.2. Automaton of the $𝚖𝚒𝚗_𝚠𝚒𝚍𝚝𝚑_𝚙𝚎𝚊𝚔$ constraint: the start of the first potential peak is discovered while triggering the transition from $s$ to $j$ , the top of a peak is discovered while triggering the transition from $j$ to $k$ , the end of a peak and the start of the next potential peak are discovered while triggering the transition from $k$ to $j$ ; the counters $W$ , $C$ and $F$ respectively stand for min_width, current and first.

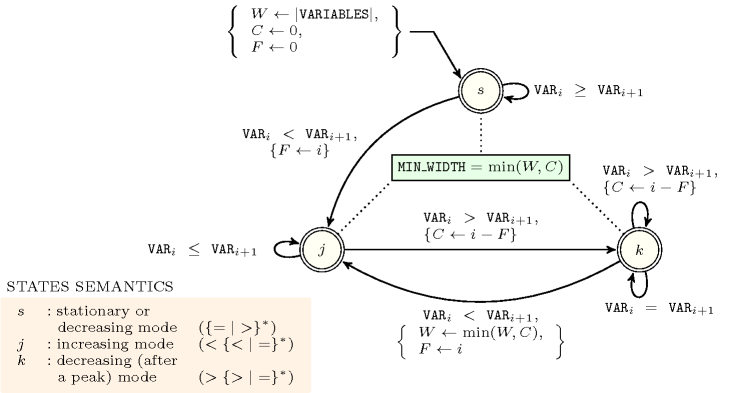
Figure 5.260.3. Glue matrix associated with the automaton of the $𝚖𝚒𝚗_𝚠𝚒𝚍𝚝𝚑_𝚙𝚎𝚊𝚔$ constraint, where $n$ stands for $| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 |$

	$s$ $({> \| =}^{*})$	$j$ $(< {< \| =}^{*})$	$k$ $(> {> \| =}^{*})$
$s$ $({> \| =}^{*})$	0	$\overset{\leftarrow}{𝙼𝙸𝙽_𝚆𝙸𝙳𝚃𝙷}$	$\overset{\leftarrow}{𝙼𝙸𝙽_𝚆𝙸𝙳𝚃𝙷}$
$j$ $(< {< \| =}^{*})$	$\vec{𝙼𝙸𝙽_𝚆𝙸𝙳𝚃𝙷}$	$min (\begin{matrix} \vec{W}, \\ n - \vec{F} - \overset{\leftarrow}{F}, \\ \overset{\leftarrow}{W} \end{matrix})$	$min (\begin{matrix} \vec{𝙼𝙸𝙽_𝚆𝙸𝙳𝚃𝙷}, \\ n - \vec{F} - \overset{\leftarrow}{F}, \\ \overset{\leftarrow}{𝙼𝙸𝙽_𝚆𝙸𝙳𝚃𝙷} \end{matrix})$
$k$ $(> {> \| =}^{*})$	$\vec{𝙼𝙸𝙽_𝚆𝙸𝙳𝚃𝙷}$	$min (\begin{matrix} \vec{𝙼𝙸𝙽_𝚆𝙸𝙳𝚃𝙷}, \\ n - \vec{F} - \overset{\leftarrow}{F}, \\ \overset{\leftarrow}{𝙼𝙸𝙽_𝚆𝙸𝙳𝚃𝙷} \end{matrix})$	$min (\begin{matrix} \vec{𝙼𝙸𝙽_𝚆𝙸𝙳𝚃𝙷}, \\ \overset{\leftarrow}{𝙼𝙸𝙽_𝚆𝙸𝙳𝚃𝙷} \end{matrix})$

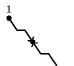
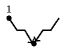
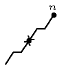
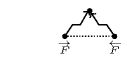
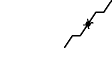
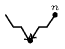
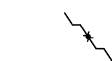
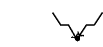
Figure 5.260.4. Illustrating the use of the state pair $(j, j)$ of the glue matrix for linking $𝙼𝙸𝙽_𝚆𝙸𝙳𝚃𝙷$ with the counters variables obtained after reading the prefix $4, 6, 7, 9$ and corresponding suffix $9, 8, 5, 4$ of the sequence $4, 6, 7, 9, 8, 5, 4$ ; note that the suffix $9, 8, 5, 4$ (in pink) is proceed in reverse order; the left (resp. right) table shows the initialisation (for $i = 0$ ) and the evolution (for $i > 0$ ) of the state of the automaton and its counters $W$ , $C$ and $F$ upon reading the prefix $4, 6, 7, 9$ (resp. the reverse suffix $4, 5, 8, 9$ ).

Figure 5.260.5. Hypergraph of the reformulation corresponding to the automaton of the $𝚖𝚒𝚗_𝚠𝚒𝚍𝚝𝚑_𝚙𝚎𝚊𝚔$ constraint

Global Constraint Catalog

5. Global Constraint Catalogue

5.260. min_width_peak

Figure 5.260.3. Glue matrix associated with the automaton of the 𝚖𝚒𝚗_𝚠𝚒𝚍𝚝𝚑_𝚙𝚎𝚊𝚔 constraint, where n stands for |𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂|

Figure 5.260.5. Hypergraph of the reformulation corresponding to the automaton of the 𝚖𝚒𝚗_𝚠𝚒𝚍𝚝𝚑_𝚙𝚎𝚊𝚔 constraint

Figure 5.260.3. Glue matrix associated with the automaton of the $𝚖𝚒𝚗_𝚠𝚒𝚍𝚝𝚑_𝚙𝚎𝚊𝚔$ constraint, where $n$ stands for $| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 |$

Figure 5.260.5. Hypergraph of the reformulation corresponding to the automaton of the $𝚖𝚒𝚗_𝚠𝚒𝚍𝚝𝚑_𝚙𝚎𝚊𝚔$ constraint