Global Constraint Catalog: Calldifferent_except

5.16. alldifferent_except_0

DESCRIPTION

LINKS

GRAPH

AUTOMATON

Origin

Derived from $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝$ .

Constraint

$𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚎𝚡𝚌𝚎𝚙𝚝_0 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

Synonyms

$𝚊𝚕𝚕𝚍𝚒𝚏𝚏_𝚎𝚡𝚌𝚎𝚙𝚝_0$ , $𝚊𝚕𝚕𝚍𝚒𝚜𝚝𝚒𝚗𝚌𝚝_𝚎𝚡𝚌𝚎𝚙𝚝_0$ .

Argument

𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂

𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛)

Restriction

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚟𝚊𝚛)

Purpose

Enforce all variables of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ to take distinct values, except those variables that are assigned value 0.

Example

(〈5, 0, 1, 9, 0, 3〉)

The $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚎𝚡𝚌𝚎𝚙𝚝_0$ constraint holds since all the values (that are different from 0) 5, 1, 9 and 3 are distinct.

All solutions

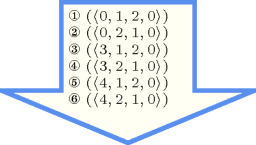
Figure 5.16.1 gives all solutions to the following non ground instance of the $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚎𝚡𝚌𝚎𝚙𝚝_0$ constraint: $V_{1} \in [0, 4]$ , $V_{2} \in [1, 2]$ , $V_{3} \in [1, 2]$ , $V_{4} \in [0, 1]$ , $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚎𝚡𝚌𝚎𝚙𝚝_0$ $(〈 V_{1}, V_{2}, V_{3}, V_{4} 〉)$ .

Figure 5.16.1. All solutions corresponding to the non ground example of the $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚎𝚡𝚌𝚎𝚙𝚝_0$ constraint of the All solutions slot

Typical

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | > 2

𝚊𝚝𝚕𝚎𝚊𝚜𝚝

(2, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 0)

𝚛𝚊𝚗𝚐𝚎

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛) > 1

Symmetries

Items of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ are permutable.
Two distinct values of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛$ that are both different from 0 can be swapped; a value of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛$ that is different from 0 can be renamed to any unused value that is also different from 0.

Arg. properties

Contractible wrt. $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ .

Usage

Quite often it appears that, for some modelling reason, you create a joker value. You do not want that normal constraints hold for variables that take this joker value. For this purpose we modify the binary arc constraint in order to discard the vertices for which the corresponding variables are assigned value 0. This will be effectively the case since all the corresponding arcs constraints will not hold.

Algorithm

An arc-consistency filtering algorithm for the $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚎𝚡𝚌𝚎𝚙𝚝_0$ constraint is described in [Cymer12]. The algorithm is based on the following ideas:

First, one can map solutions of the $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚎𝚡𝚌𝚎𝚙𝚝_0$ constraint to var-perfect matchingsA var-perfect matching is a maximum matching covering all vertices representing variables. in a bipartite graph derived from the domain of the variables of the constraint in the following way: to each variable of the $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚎𝚡𝚌𝚎𝚙𝚝_0$ constraint corresponds a variable and a joker vertices, while to each potential value corresponds a value vertex; there is an edge between a variable vertex and a value vertex if and only if that value belongs to the domain of the corresponding variable; there is an edge between a variable vertex and its corresponding value vertex.
Second, Dulmage-Mendelsohn decomposition [DulmageMendelsohn58] is used to characterise all edges that do not belong to any var-perfect matching, and therefore prune the corresponding variables.

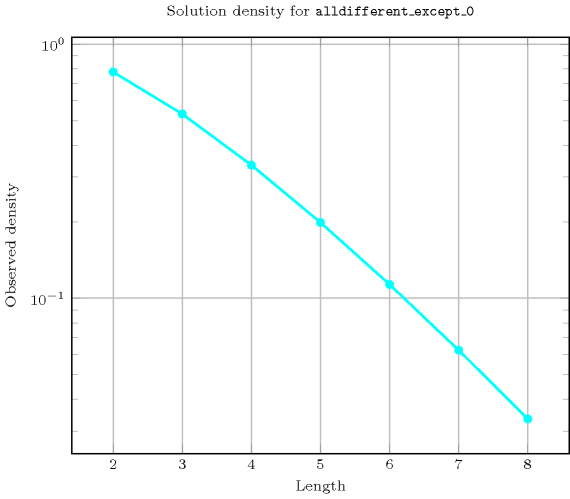
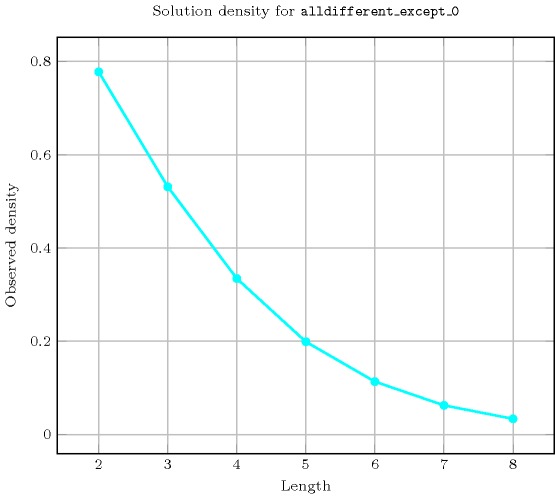
Counting

Length ( $n$ )	2	3	4	5	6	7	8
Solutions	7	34	209	1546	13327	130922	1441729

Number of solutions for $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚎𝚡𝚌𝚎𝚙𝚝_0$ : domains $0 . . n$

ctrs/alldifferent_except_0-2-tikz

ctrs/alldifferent_except_0-3-tikz

hard version: $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝$ .

implied by: $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝$ .

implies: $𝚖𝚞𝚕𝚝𝚒_𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚘𝚗𝚝𝚒𝚐𝚞𝚒𝚝𝚢$ .

Keywords

characteristic of a constraint: joker value, all different, sort based reformulation, automaton, automaton with array of counters.

constraint type: value constraint, relaxation.

filtering: bipartite matching, arc-consistency.

final graph structure: one_succ.

Arc input(s)

$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$

Arc generator

𝐶𝐿𝐼𝑄𝑈𝐸

\mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 1, 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 2)

Arc arity

Arc constraint(s)

• 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 1 . 𝚟𝚊𝚛 \neq 0

• 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 1 . 𝚟𝚊𝚛 = 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 2 . 𝚟𝚊𝚛

Graph property(ies)

𝐌𝐀𝐗_𝐍𝐒𝐂𝐂

\leq 1

Graph model

The graph model is the same as the one used for the $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝$ constraint, except that we discard all variables that are assigned value 0.

Parts (A) and (B) of Figure 5.16.2 respectively show the initial and final graph associated with the Example slot. Since we use the $𝐌𝐀𝐗_𝐍𝐒𝐂𝐂$ graph property we show one of the largest strongly connected components of the final graph. The $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚎𝚡𝚌𝚎𝚙𝚝_0$ holds since all the strongly connected components have at most one vertex: a value different from 0 is used at most once.

Figure 5.16.2. Initial and final graph of the $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚎𝚡𝚌𝚎𝚙𝚝_0$ constraint


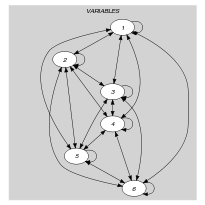
(a)	(b)

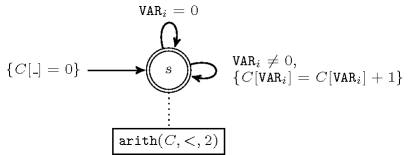
Automaton: Figure 5.16.3 depicts the automaton associated with the $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚎𝚡𝚌𝚎𝚙𝚝_0$ constraint. To each variable ${𝚅𝙰𝚁}_{i}$ of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ corresponds a 0-1 signature variable $𝚂_{i}$ . The following signature constraint links ${𝚅𝙰𝚁}_{i}$ and $𝚂_{i}$ : ${𝚅𝙰𝚁}_{i} \neq 0 \Leftrightarrow 𝚂_{i}$ . The automaton counts the number of occurrences of each value different from 0 and finally imposes that each non-zero value is taken at most one time.

Figure 5.16.3. Automaton of the $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚎𝚡𝚌𝚎𝚙𝚝_0$ constraint

Global Constraint Catalog

5. Global Constraint Catalogue

5.16. alldifferent_except_0

Figure 5.16.1. All solutions corresponding to the non ground example of the $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚎𝚡𝚌𝚎𝚙𝚝_0$ constraint of the All solutions slot

Figure 5.16.2. Initial and final graph of the $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚎𝚡𝚌𝚎𝚙𝚝_0$ constraint

Figure 5.16.3. Automaton of the $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚎𝚡𝚌𝚎𝚙𝚝_0$ constraint

Global Constraint Catalog

5. Global Constraint Catalogue

5.16. alldifferent_except_0

Figure 5.16.1. All solutions corresponding to the non ground example of the 𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚎𝚡𝚌𝚎𝚙𝚝_0 constraint of the All solutions slot

Figure 5.16.2. Initial and final graph of the 𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚎𝚡𝚌𝚎𝚙𝚝_0 constraint

Figure 5.16.3. Automaton of the 𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚎𝚡𝚌𝚎𝚙𝚝_0 constraint

Figure 5.16.1. All solutions corresponding to the non ground example of the $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚎𝚡𝚌𝚎𝚙𝚝_0$ constraint of the All solutions slot

Figure 5.16.2. Initial and final graph of the $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚎𝚡𝚌𝚎𝚙𝚝_0$ constraint

Figure 5.16.3. Automaton of the $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚎𝚡𝚌𝚎𝚙𝚝_0$ constraint