Global Constraint Catalog: Cdisjunctive_or_same

5.127. disjunctive_or_same_end

DESCRIPTION

LINKS

GRAPH

Origin

Scheduling.

Constraint

$𝚍𝚒𝚜𝚓𝚞𝚗𝚌𝚝𝚒𝚟𝚎_𝚘𝚛_𝚜𝚊𝚖𝚎_𝚎𝚗𝚍 (𝚃𝙰𝚂𝙺𝚂)$

Synonyms

$𝚜𝚊𝚖𝚎_𝚎𝚗𝚍_𝚘𝚛_𝚍𝚒𝚜𝚓𝚞𝚗𝚌𝚝𝚒𝚟𝚎$ , $𝚗𝚘𝚗_𝚘𝚟𝚎𝚛𝚕𝚊𝚙_𝚘𝚛_𝚜𝚊𝚖𝚎_𝚎𝚗𝚍$ , $𝚜𝚊𝚖𝚎_𝚎𝚗𝚍_𝚘𝚛_𝚗𝚘𝚗_𝚘𝚟𝚎𝚛𝚕𝚊𝚙$ .

Argument

𝚃𝙰𝚂𝙺𝚂

𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚘𝚛𝚒𝚐𝚒𝚗 - 𝚍𝚟𝚊𝚛, 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗 - 𝚍𝚟𝚊𝚛)

Restrictions

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚃𝙰𝚂𝙺𝚂, [𝚘𝚛𝚒𝚐𝚒𝚗, 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗])

𝚃𝙰𝚂𝙺𝚂 . 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗 \geq 0

Purpose

All pairs of tasks of the collection $𝚃𝙰𝚂𝙺𝚂$ that have a duration strictly greater than 0 should either not overlap either have the same end, i.e. $\forall i \in [1, | 𝚃𝙰𝚂𝙺𝚂 |], \forall j \in [i + 1, | 𝚃𝙰𝚂𝙺𝚂 |] :$ $𝚃𝙰𝚂𝙺𝚂 [i] . 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗 = 0 \lor 𝚃𝙰𝚂𝙺𝚂 [j] . 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗 = 0 \lor 𝚃𝙰𝚂𝙺𝚂 [i] . 𝚘𝚛𝚒𝚐𝚒𝚗 + 𝚃𝙰𝚂𝙺𝚂 [i] . 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗 \leq 𝚃𝙰𝚂𝙺𝚂 [j] . 𝚘𝚛𝚒𝚐𝚒𝚗 \lor 𝚃𝙰𝚂𝙺𝚂 [j] . 𝚘𝚛𝚒𝚐𝚒𝚗 + 𝚃𝙰𝚂𝙺𝚂 [j] . 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗 \leq 𝚃𝙰𝚂𝙺𝚂 [i] . 𝚘𝚛𝚒𝚐𝚒𝚗 \lor 𝚃𝙰𝚂𝙺𝚂 [i] . 𝚘𝚛𝚒𝚐𝚒𝚗 + 𝚃𝙰𝚂𝙺𝚂 [i] . 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗 = 𝚃𝙰𝚂𝙺𝚂 [j] . 𝚘𝚛𝚒𝚐𝚒𝚗 + 𝚃𝙰𝚂𝙺𝚂 [j] . 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗$ .

Example

(\begin{matrix} 〈\begin{matrix} 𝚘𝚛𝚒𝚐𝚒𝚗 - 4 & 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗 - 3, \\ 𝚘𝚛𝚒𝚐𝚒𝚗 - 7 & 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗 - 2, \\ 𝚘𝚛𝚒𝚐𝚒𝚗 - 5 & 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗 - 2 \end{matrix}〉 \end{matrix})

Since the ends of the first and third tasks coincide, and since the second task does neither overlap the first task nor the third task, the $𝚍𝚒𝚜𝚓𝚞𝚗𝚌𝚝𝚒𝚟𝚎_𝚘𝚛_𝚜𝚊𝚖𝚎_𝚎𝚗𝚍$ constraint holds.

Typical

| 𝚃𝙰𝚂𝙺𝚂 | > 2

𝚃𝙰𝚂𝙺𝚂 . 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗 \geq 1

Symmetries

Items of $𝚃𝙰𝚂𝙺𝚂$ are permutable.
$𝚃𝙰𝚂𝙺𝚂 . 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗$ can be decreased to any value $\geq 0$ .
One and the same constant can be added to the $𝚘𝚛𝚒𝚐𝚒𝚗$ attribute of all items of $𝚃𝙰𝚂𝙺𝚂$ .

Arg. properties

Contractible wrt. $𝚃𝙰𝚂𝙺𝚂$ .

implied by: $𝚍𝚒𝚜𝚓𝚞𝚗𝚌𝚝𝚒𝚟𝚎$ .

Keywords

constraint type: scheduling constraint, resource constraint, decomposition.

modelling: disjunction, zero-duration task.

Arc input(s)

$𝚃𝙰𝚂𝙺𝚂$

Arc generator

𝐶𝐿𝐼𝑄𝑈𝐸

(<) \mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚝𝚊𝚜𝚔𝚜 1, 𝚝𝚊𝚜𝚔𝚜 2)

Arc arity

Arc constraint(s)

⋁ (\begin{matrix} 𝚝𝚊𝚜𝚔𝚜 1 . 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗 = 0, \\ 𝚝𝚊𝚜𝚔𝚜 2 . 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗 = 0, \\ 𝚝𝚊𝚜𝚔𝚜 1 . 𝚘𝚛𝚒𝚐𝚒𝚗 + 𝚝𝚊𝚜𝚔𝚜 1 . 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗 \leq 𝚝𝚊𝚜𝚔𝚜 2 . 𝚘𝚛𝚒𝚐𝚒𝚗, \\ 𝚝𝚊𝚜𝚔𝚜 2 . 𝚘𝚛𝚒𝚐𝚒𝚗 + 𝚝𝚊𝚜𝚔𝚜 2 . 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗 \leq 𝚝𝚊𝚜𝚔𝚜 1 . 𝚘𝚛𝚒𝚐𝚒𝚗, \\ \begin{matrix} 𝚝𝚊𝚜𝚔𝚜 1 . 𝚘𝚛𝚒𝚐𝚒𝚗 + 𝚝𝚊𝚜𝚔𝚜 1 . 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗 = \\ 𝚝𝚊𝚜𝚔𝚜 2 . 𝚘𝚛𝚒𝚐𝚒𝚗 + 𝚝𝚊𝚜𝚔𝚜 2 . 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗 \end{matrix} \end{matrix})

Graph property(ies)

𝐍𝐀𝐑𝐂

= | 𝚃𝙰𝚂𝙺𝚂 | * (| 𝚃𝙰𝚂𝙺𝚂 | - 1) / 2

Graph model

We generate a clique with a non-overlapping constraint or a same end constraint between each pair of distinct tasks and state that the number of arcs of the final graph should be equal to the number of arcs of the initial graph.

Parts (A) and (B) of Figure 5.127.1 respectively show the initial and final graph associated with the Example slot. The $𝚍𝚒𝚜𝚓𝚞𝚗𝚌𝚝𝚒𝚟𝚎_𝚘𝚛_𝚜𝚊𝚖𝚎_𝚎𝚗𝚍$ constraint holds since all the arcs of the initial graph belong to the final graph.

Figure 5.127.1. Initial and final graph of the $𝚍𝚒𝚜𝚓𝚞𝚗𝚌𝚝𝚒𝚟𝚎_𝚘𝚛_𝚜𝚊𝚖𝚎_𝚎𝚗𝚍$ constraint


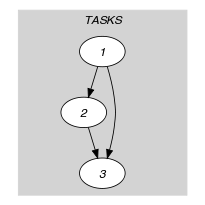
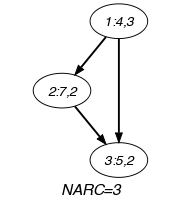
(a)	(b)

Global Constraint Catalog

5. Global Constraint Catalogue

5.127. disjunctive_or_same_end

Figure 5.127.1. Initial and final graph of the 𝚍𝚒𝚜𝚓𝚞𝚗𝚌𝚝𝚒𝚟𝚎_𝚘𝚛_𝚜𝚊𝚖𝚎_𝚎𝚗𝚍 constraint

Figure 5.127.1. Initial and final graph of the $𝚍𝚒𝚜𝚓𝚞𝚗𝚌𝚝𝚒𝚟𝚎_𝚘𝚛_𝚜𝚊𝚖𝚎_𝚎𝚗𝚍$ constraint