5.392. sum_set
| DESCRIPTION | LINKS | GRAPH |
- Origin
H. Cambazard
- Constraint
- Arguments
- Restrictions
- Purpose
Let denote the sum of the attributes of the collection for which the corresponding values occur in the set . Enforce the following constraint to hold: .
- Example
-
The constraint holds since the sum of the attributes for which the corresponding attribute belongs to the first argument is equal (i.e., since is set to ) to its last argument .
- Typical
- Symmetry
Items of are permutable.
- Systems
- See also
common keyword: , (sum).
- Keywords
characteristic of a constraint: sum.
constraint arguments: binary constraint, constraint involving set variables.
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
- Graph property(ies)
-
- Graph model
Parts (A) and (B) of Figure 5.392.1 respectively show the initial and final graph associated with the Example slot.
Figure 5.392.1. Initial and final graph of the constraint
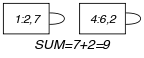
(a) (b)